* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 1 Electrostatics Lecture No : 14 Tittle : Faraday`s Law of Induction
Condensed matter physics wikipedia , lookup
Electrostatics wikipedia , lookup
Field (physics) wikipedia , lookup
Neutron magnetic moment wikipedia , lookup
Maxwell's equations wikipedia , lookup
Magnetic field wikipedia , lookup
Magnetic monopole wikipedia , lookup
History of electromagnetic theory wikipedia , lookup
Electromagnetism wikipedia , lookup
Superconductivity wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
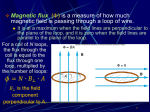
Course : Bachelor of Applied Physical Science IInd Year (Semester IV) Paper no : 14 Subject : PHPT – 404 Electricity, Magnetism and Electromagnetic Theory Topic No. & Title : Topic – 1 Electrostatics Lecture No : 14 Tittle : Faraday’s Law of Induction Introduction Hello friends, previously we have been discussing the fact that a current produces a magnetic field. That fact came as a surprise to the scientists who discovered the effect. Perhaps even more surprising was the discovery of the reverse effect: A magnetic field can produce an electric field that can drive a current. This link between a magnetic field and the electric field it produces is now called Faraday’s law of induction. The observations by Michael Faraday and other scientists that led to this law were at first just basic science. Today, however, applications of that basic science are almost everywhere. For example, electric generators that power cities, huge induction furnaces that are commonplace in foundries. Before we actually get to the applications such as electric generators, we must examine two simple experiments about Faraday’s law of induction. First Experiment Figure shows a conducting loop connected to a sensitive ammeter. Because there is no battery or other source of emf included, there is no current in the circuit. However, if we move a bar magnet toward the loop, a current suddenly appears in the circuit. The current disappears when the magnet stops. If we then move the magnet away, a current again suddenly appears, but now in the opposite direction. If we experimented for a while, we would discover the following: 1. A current appears only if there is relative motion between the loop and the magnet (one must move relative to the other); the current disappears when the relative motion between them ceases. 2. Faster motion produces a greater current. 3. If moving the magnet’s North Pole toward the loop causes, say, clockwise current, then moving the North Pole away causes counterclockwise current. Moving the South Pole toward or away from the loop also causes currents, but in the reversed directions. The current produced in the loop is called an induced current; the work done per unit charge to produce that current (to move the conduction electrons that constitute the current) is called an induced emf; and the process of producing the current and emf is called induction. Second Experiment For this experiment we use the apparatus as shown, with the two conducting loops close to each other but not touching. If we close switch S, to turn on a current in the right-hand loop, the meter suddenly and briefly registers a current — an induced current — in the left-hand loop. If we then open the switch, another sudden and brief induced current appears in the left-hand loop, but in the opposite direction. We get an induced current (and thus an induced emf) only when the current in the right-hand loop is changing (either turning on or turning off) and not when it is constant (even if it is large). The induced emf and induced current in these experiments are apparently caused when something changes — but what is that “something”? We are going to discuss that something in next section. Faraday’s Law of Induction Faraday realized that an emf and a current can be induced in a loop, as in our two experiments, by changing the amount of magnetic field passing through the loop. He further realized that the “amount of magnetic field” can be visualized in terms of the magnetic field lines passing through the loop. Faraday’s law of induction, stated in terms of our experiments, is: An emf is induced in the loop when the number of magnetic field lines that pass through the loop is changing. The actual number of field lines passing through the loop does not matter; the values of the induced emf and induced current are determined by the rate at which that number changes. In our first experiment, the magnetic field lines spread out from the north pole of the magnet. Thus, as we move the North Pole closer to the loop, the number of field lines passing through the loop increases. That increase apparently causes conduction electrons in the loop to move (the induced current) and provides energy (the induced emf) for their motion. When the magnet stops moving, the number of field lines through the loop no longer changes and the induced current and induced emf disappear. In our second experiment, when the switch is open i.e. no current, there are no field lines. However, when we turn on the current in the right-hand loop, the increasing current builds up a magnetic field around that loop and at the left-hand loop. While the field builds, the number of magnetic field lines through the left-hand loop increases. As in the first experiment, the increase in field lines through that loop apparently induces a current and an emf there. When the current in the right-hand loop reaches a final, steady value, the number of field lines through the left-hand loop no longer changes, and the induced current and induced emf disappear. A Quantitative Treatment To put Faraday’s law to work, we need a way to calculate the amount of magnetic field that passes through a loop. In a similar situation while discussing electric fields, we needed to calculate the amount of electric field that passes through a surface. There we defined an electric flux. ϕ𝐸 = ∫ 𝐸⃗ ∙ 𝑑𝐴 Here we define a magnetic flux: Suppose a loop enclosing an area A is placed in a magnetic field. Then the magnetic flux through the loop is ⃗ ∙ 𝑑𝐴 … A ϕ𝐵 = ∫ 𝐵 Suppose that the loop lies in a plane and that the magnetic field is perpendicular to the plane of the loop. Then we can write the dot product in Eq. A as 𝐵 𝑑𝐴 𝑐𝑜𝑠 0 = 𝐵 𝑑𝐴. If the magnetic field is also uniform, then B can be brought out in front of the integral sign. The remaining integral then gives just the area A of the loop. Thus, Eq. A reduces to ϕ𝐵 = 𝐵𝐴 With this notion of magnetic flux, we can state Faraday’s law in a more quantitative and useful way as: The magnitude of the emf induced in a conducting loop is equal to the rate at which the magnetic flux through that loop changes with time. As we will see below, the induced emf tends to oppose the flux change, so Faraday’s law is formally written as 𝜀=− 𝑑ϕ𝐵 …𝐵 𝑑𝑡 Here the minus sign indicates the opposition. We often neglect the minus sign in Eq. B, seeking only the magnitude of the induced emf. If we change the magnetic flux through a coil of N turns, an induced emf appears in every turn and the total emf induced in the coil is the sum of these individual induced emfs. If the coil is tightly wound, so that the same magnetic flux passes through all the turns, the total emf induced in the coil is 𝜀 = −𝑁 𝑑ϕ𝐵 𝑑𝑡 The general means by which we can change the magnetic flux through a coil are: 1. Change the magnitude B of the magnetic field within the coil. 2. Change either the total area of the coil or the portion of that area that lies within the magnetic field (for example, by expanding the coil or sliding it into or out of the field). 3. Change the angle between the direction of the magnetic field and the plane of the coil (for example, by rotating the coil so that field is first perpendicular to the plane of the coil and then is along that plane). Applications of Faraday’s Law The ground fault circuit interrupter is an interesting safety device that protects users of electrical appliances against electric shock. Its operation makes use of Faraday’s law. In the ground fault circuit interrupter shown, wire 1 leads from the wall outlet to the appliance to be protected and wire 2 leads from the appliance back to the wall outlet. An iron ring surrounds the two wires, and a sensing coil is wrapped around part of the ring. Because the currents in the wires are in opposite directions and of equal magnitude, there is no magnetic field surrounding the wires and the net magnetic flux through the sensing coil is zero. If the return current in wire 2 changes so that the two currents are not equal, however, circular magnetic field lines exist around the pair of wires. (That can happen if, for example, the appliance becomes wet, enabling current to leak to ground.) Therefore, the net magnetic flux through the sensing coil is no longer zero. Because household current is alternating (meaning that its direction keeps reversing), the magnetic flux through the sensing coil changes with time, inducing an emf in the coil. This induced emf is used to trigger a circuit breaker, which stops the current before it is able to reach a harmful level. Another interesting application of Faraday’s law is the production of sound in an electric guitar. The coil in this case, called the pickup coil, is placed near the vibrating guitar string, which is made of a metal that can be magnetized. A permanent magnet inside the coil magnetizes the portion of the string nearest the coil. When the string vibrates at some frequency, its magnetized segment produces a changing magnetic flux through the coil. The changing flux induces an emf in the coil that is fed to an amplifier. The output of the amplifier is sent to the loudspeakers, which produce the sound waves we hear. Lenz’s Law Soon after Faraday proposed his law of induction, Heinrich Friedrich Lenz devised a rule for determining the direction of an induced current in a loop that is: An induced current has a direction such that the magnetic field due to the current opposes the change in the magnetic flux that induces the current. This means that, the induced current tends to keep the original magnetic flux through the loop from changing. Furthermore, the direction of an induced emf is that of the induced current. The key word in Lenz’s law is “opposition.” Let’s apply the law to the motion of the North Pole toward the conducting loop. Opposition to Pole Movement The approach of the magnet’s North Pole in Fig. increases the magnetic flux through the loop and thereby induces a current in the loop. The loop then acts as a magnetic dipole with a south pole and a north pole, and its magnetic dipole moment is directed from south to north. To oppose the magnetic flux increase being caused by the approaching magnet, the loop’s North Pole and thus the magnetic dipole moment must face toward the approaching North Pole so as to repel it. Then the curled – straight right-hand rule for tells us that the current induced in the loop must be counterclockwise. If we next pull the magnet away from the loop, a current will again be induced in the loop. Now, however, the loop will have a South Pole facing the retreating north pole of the magnet, so as to oppose the retreat. Thus, the induced current will be clockwise. Opposition to Flux Change With the magnet initially distant, no magnetic flux passes through the loop. As the north pole of the magnet then nears the loop with its magnetic field directed downward, the flux through the loop increases. To oppose this increase in flux, the induced current i must set up its own field directed upward inside the loop. Then the upward flux of field opposes the increasing downward flux of field. The curled – straight right-hand rule then tells us that I must be counterclockwise. So friends here we come to the end of our discussion in this lecture today and therefore we sum up: Faraday’s Law of Induction states that if the magnetic flux through an area bounded by a closed conducting loop changes with time, a current and an emf are produced in the loop; this process is called induction. Lenz’s Law states that an induced current has a direction such that the magnetic field due to the current opposes the change in the magnetic flux that induces the current. The induced emf has the same direction as the induced current. So that is it for today. See you in the next lecture we shall be discussing more about magnetostatics. Thank you very much. OBJECTIVE The objective of this lecture is to make the students of B.Sc. Computers understand Faraday’s Law. Course : Bachelor of Applied Physical Science IInd Year (Semester IV) Paper no : 14 Subject : PHPT – 404 Electricity, Magnetism and Electromagnetic Theory Topic No. & Title : Topic – 1 Electrostatics Lecture No : 14 Tittle : Faraday’s Law of Induction SUMMARY Faraday’s Law of Induction states that if the magnetic flux through an area bounded by a closed conducting loop changes with time, a current and an emf are produced in the loop; this process is called induction. Lenz’s Law states that an induced current has a direction such that the magnetic field due to the current opposes the change in the magnetic flux that induces the current. The induced emf has the same direction as the induced current. Course : Bachelor of Applied Physical Science IInd Year (Semester IV) Paper no : 14 Subject : PHPT – 404 Electricity, Magnetism and Electromagnetic Theory Topic No. & Title : Topic – 1 Electrostatics Lecture No : 14 Tittle : Faraday’s Law of Induction FAQs Q1. What is power-frequency EMF and how does it compare to other types of Fields ? Ans : The electromagnetic spectrum (right) covers an enormous range of frequencies. These frequencies are expressed in cycles per second (i.e., Hz). Electric power (60 Hz in North America, 50 Hz in most other places) is in the extremely low frequency range, which includes frequencies below 3000 Hz. The higher the frequency, the shorter the distance between one wave and the next, and the greater the amount of energy in the field. Microwave frequency fields, with wavelengths of several inches, have enough energy to cause heating in conducting material. Still higher frequencies like X-rays cause ionization-the breaking of molecular bonds, which damages genetic material. In comparison, power frequency fields have wavelengths of more than 3100 miles (5000 km) and consequently have very low energy levels that do not cause heating or ionization. However, AC fields do create weak electric currents in conducting objects, including people and animals. Q2. What is Faraday’s Law ? Ans : Electromagnetic induction (or sometimes just induction) is a process where a conductor placed in a changing magnetic field (or a conductor moving through a stationary magnetic field) causes the production of a voltage across the conductor. This process of electromagnetic induction, in turn, causes an electrical current - it is said to induce the current. Michael Faraday is given credit for the discovery of electromagnetic induction in 1831, though some others had noted similar behavior in the years prior to this. The formal name for the physics equation that defines the behavior of an induced electromagnetic field from the magnetic flux (change in a magnetic field) is Faraday's law of electromagnetic induction. Q3. Does the process of electromagnetic induction work in reverse ? Ans : Yes the process of electromagnetic induction works in reverse as well, so that a moving electrical charge generates a magnetic field. In fact, a traditional magnet is the result of the individual motion of the electrons within the individual atoms of the magnet, aligned so that the generated magnetic field is in a uniform direction. (In non-magnetic materials, the electrons move in such a way that the individual magnetic fields point in different directions, so they cancel each other out and the net magnetic field generated is negligible.) The more generalized equation is one of Maxwell's equations, called the MaxwellFaraday equation, which defines the relationship between changes in electrical fields and magnetic fields. Q4. What is emf ? Ans : In physics, electromotive force, or most commonly emf is something that which tends to cause current to flow." More formally, emf is the external work expended per unit of charge to produce an electric potential difference across two open-circuited terminals. Separating positive and negative charges, thereby generating an electric field, creates the electric potential difference. The created electrical potential difference drives current flow if a circuit is attached to the source of emf. When current flows, however, the voltage across the terminals of the source of emf is no longer the open-circuit value, due to voltage drops inside the device due to its internal resistance. Devices that can provide emf include voltaic cells, thermoelectric devices, solar cells, electrical generators, and transformers. In nature, emf is generated whenever magnetic field fluctuations occur through a surface. An example for this is the varying Earth magnetic field during a geomagnetic storm, acting on anything on the surface of the planet, likes an extended electrical grid. In the case of a battery, charge separation that gives rise to a voltage difference is accomplished by chemical reactions at the electrodes; a voltaic cell can be thought of as having a "charge pump" of atomic dimensions at each electrode, that is: "A source of emf can be thought of as a kind of charge pump that acts to move positive charge from a point of low potential through its interior to a point of high potential. … By chemical, mechanical or other means, the source of emf performs work on that charge to move it to the high potential terminal. 1. A sensitive ammeter is connected to a wire loop and placed within the magnetic field of a strong horseshoe magnet. The ammeter shows a deflection when : A. The wire is moved parallel to the field. B. The wire is moved perpendicularly to the field. C. Neither wire nor magnet is moving. D. The wire's axis is parallel to the field. 2. According to Lenz's law the direction of an induced current in a conductor will be that which tends to produce which of the following effects ? A. Enhance the effect, which produces it B. Produce a greater heating effect C. Produce the greatest voltage D. Oppose the effect, which produces it 3. "GFI" stands for: A. Grand flux indicator. B. Ground forcing indicator. C. Ground fault interrupter. D. Gauss-free invention. 4. The principle or law that says, an induced emf in a circuit loop produces a current whose magnetic field opposes further change of magnetic flux" is credited to: A. Faraday. B. Lenz. C. Ampere. D. Maxwell. Course : Bachelor of Applied Physical Science IInd Year (Semester IV) Paper no : 14 Subject : PHPT – 404 Electricity, Magnetism and Electromagnetic Theory Topic No. & Title : Topic – 1 Electrostatics Lecture No : 14 Tittle : Faraday’s Law of Induction Glossary Electromagnetic induction: The process in which current is induced in a coil whenever there is a change in the magnetic flux linked with the coil. Lenz's law: The induced current always flows in such a direction that it opposes the cause producing it. Magnetic reversal: The changing of polarity of the earth's magnetic field as the north magnetic pole and the south magnetic pole exchange positions. Vector Quantity: A quantity, which needs both magnitude and direction to describe it. Voltage drop: A quantity, which needs both magnitude and direction to describe it. Assignment A certain elastic conducting material is stretched into a circular loop of 12.0 cm radius. It is placed with its plane perpendicular to a uniform 0.800 T magnetic field. When released, the radius of the loop starts to shrink at an instantaneous rate of 75.0 cm/s. What emf is induced in the loop at that instant ? Course : Bachelor of Applied Physical Science IInd Year (Semester IV) Paper no : 14 Subject : PHPT – 404 Electricity, Magnetism and Electromagnetic Theory Topic No. & Title : Topic – 1 Electrostatics Lecture No : 14 Tittle : Faraday’s Law of Induction References 1. Fundamentals of electricity and magnetism By Arthur F. Kip (McGraw-Hill, 1968) 2. Electricity and magnetism by J.H.Fewkes & John Yarwood. Vol. I (Oxford Univ. Press, 1991). 3. Introduction to Electrodynamics, 3rd edition, by David J. Griffiths, (Benjamin Cummings,1998). 4. Electricity and magnetism By Edward M. Purcell (McGraw-Hill Education, 1986) 5. Electricity and magnetism. By D C Tayal (Himalaya Publishing House,1988) 6. Electromagnetics by Joseph A.Edminister 2nd ed.(New Delhi: Tata Mc Graw Hill, 2006). Links http://phun.physics.virginia.edu/topics/electrostatics.html http://www.sciencedirect.com/science/journal/ http://web.mit.edu/8.02t/www/802TEAL3D/visualizations/electrostatics/