Download Force

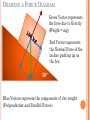
DYNAMICS
THE CAUSES OF MOTION
Mr. Rockensies
Regents Physics
INTRODUCTION
Motion is caused by Force.
Force – any push or pull on an object
• Symbol - F
F = ma, where F is a Force, m is a mass, and
a is an acceleration
TYPES OF FORCES
Contact Forces – touch the
object
1. Normal Force (FN) –
contact force which is
perpendicular to the
contact surface
2. Friction Force (Ff) –
contact force which is
parallel to the contact
surface
3. Tension (FT) – force
through a rope, cable,
chain, etc. can only pull
Remote Forces – act from
a distance
1. Gravity (Fg) – Weight
2. Static Electricity (FE)
3. Magnetism (FB or FM)
4. Nuclear Forces
UNITS
 Forces
are measured in Newtons, N
 1 kg weighs about 10 N, 100 g
weighs 1 N

Remember back to the lab we did
Forces are vectors – have magnitude
and direction
Just like with projectile motion, we
will need to break down resultants
into its components, and find the
resultant when given components.
Mass – amount of matter
Weight – force experienced by that matter
Mass ≠ Weight
Mass – measured on a balance
Force – measured on a scale using a spring
Equilibrium – “equal forces”, forces which are
balanced or add to zero
A breeze blowing to the east pushes a sailboat along a
calm ocean with a force of 400 N. The boat has a mass of
1000 kg. What is the acceleration felt by the boat?
F = 400 N
m = 1000 kg
F = ma
400 N = (1000 kg)a
a = 400 N/1000 kg
a = 0.4 m/s2
A man pushes a cart with a mass of 50 kg along an even,
frictionless surface. The cart accelerates at a rate of 4
m/s2. What is the force the man pushes the cart with?
m = 50 kg
a = 4 m/s2
F = ma
F = (50 kg)(4 m/s2)
F = 200 N
HOW DO WE DERIVE THE UNITS??
If we start with the equation, F = ma, we can replace
the variables with their appropriate units.
F = (kg)(m/s2)
F = kg•m = N
s2
FORCE VECTORS
Resultant – the addition of two vectors
For Force, we use the symbol FNET OR FR
When there is a net force, FNET, that is not equal to
zero, it is said to be unbalanced. This indicates that
an object is accelerating because there is a force
acting on it.
When we look at the forces acting on an object, we
draw them concurrently.
Resultant vectors are found using either:
a) Pythagorean Theorem + SOHCAHTOA for right angles
b) by drawing vectors to scale for any other angles (Like in
the Combining Forces Lab (#9)
F2
FNET
F1
E
E = Equilibrant – a single force
which brings about equilibrium. It is
equal to the resultant but opposite in
direction
MAXIMUM RESULTANT
Forces in the same direction or zero degrees apart
7N
5N
equals
12 N
MINIMUM RESULTANT
Opposite direction, 180° apart
5N
•
7N
equals
2N
Every number between 2 and 12 is a possible resultant. The
equilibrant then would also be between 2 and 12, but in the opposite
direction.
ONLINE EXAMPLES
Resultant versus Equilibrant
Drawing Components
Calculate the Magnitude of the Resultant
COMPONENTS
All forces can be resolved into horizontal and vertical components.
Case 1: Inclined Force on an object on a level surface
Fy = sin θ
F
Fx = Fcosθ
Fx moves the box
Fy lifts the box
Case 2: Block on an inclined plane
FNormal
Fperpendicular(F|) = Fgcosθ
FN = F|
FParallel
FPerpendicular
FGravity
Fparallel (F||) causes sliding
F|| = Fgsinθ
PRACTICE PROBLEM 1 (PART 1)
A 50 kg sled is pulled by a boy across a
smooth, icy surface. If the boy is pulling
the sled 500 N at 30° above the horizontal,
what is the horizontal component of the
force?
30°
sled
PRACTICE PROBLEM 1 (PART 2)
What is the acceleration experienced
by the sled?
Does the vertical component of the
force affect the acceleration?
sled
ANSWERS
Ax = Acosθ
Fx = (500 N)cos(30°)
Fx = 430 N
FNET = ma
430 N = (50 kg)a
a = 8.6 m/s2
The vertical component doesn’t affect
acceleration. It only causes the object to
lift off the ground, rather than move it
backward or forward.
PRACTICE PROBLEM 1 (PART 3)
Using the same sled from the previous
example, what is the weight of the sled?
Find the vertical component of the force
pulling the sled. Would this force cause
the sled to lift of the ground? Why?
sled
PRACTICE PROBLEM 1 (PART 4)
What is the Normal Force felt by the
sled?
sled
ANSWERS
Weight is equal to Fg. Fg = mg. Since the
mass of the sled is 50 kg, we can find
weight by plugging in the numbers and
solving for Fg.
Fg = (50 kg)(9.81 m/s2)
Fg = 490 N down
This would not be enough
Ay = Asinθ
to lift the sled because
Fy = 500 N sin(30°) the force due to gravity is
Fy = 250 N up
much greater.
ANSWERS
The Normal Force felt by the sled would
be equal in magnitude to the
Gravitational Force (Weight), but in the
opposite direction (perpendicular to the
surface).
Therefore, FN = 490 N up
PRACTICE PROBLEM 2 (PART 1)
A block with a mass of 100 kg is at rest on
an inclined plane with an angle of 30°.
What is the weight of the block?
What is the parallel force of the block?
What is the perpendicular force of the
block?
30°
DRAWING A FORCE DIAGRAM
Green Vector represents
the force due to Gravity
(Weight = mg)
Red Vector represents
the Normal Force of the
incline pushing up on
the box
30°
Blue Vectors represent the components of the weight
(Perpendicular and Parallel Forces)
ANSWERS
The Weight of the block is equal to mass times
acceleration due to gravity.
W = mg
W = (100 kg)(9.8 m/s2)
W = 980 N
F|| = Fg sinθ
F|| = (980 N)sin(30°)
F|| = 490 N
F| = Fg cosθ
F| = (980 N)cos(30°)
F| = 850 N
PRACTICE PROBLEM 2 (PART 2)
What is the acceleration of the block as it
slides down the inclined plane?
What is the Normal Force felt by the block?
As the angle of the inclined plane increases,
what happens to the parallel and
perpendicular forces?
30°
ANSWERS
To find the acceleration of the block as it slides
down the incline, we need to use the parallel
force.
F|| = ma
490 N = (100 kg)a
a = 4.9 m/s2
Normal Force is equal to the Perpendicular Force,
but opposite in direction.
FN = 850 N