* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download mathematics 1º eso - IES Miguel de Cervantes
Survey
Document related concepts
Transcript
MATHEMATICS 1º ESO
I.E.S. “Miguel de Cervantes”
ALUMNO/A:________________________________
CURSO:___________
1
UNIT 1: NATURAL NUMBERS…………………………………on page 2
UNIT 2: DIVISIBILITY……………………………………………..on page 13
UNIT 3: FRACTIONS……………………………………………….on page 26
UNIT 4: DECIMAL NUMBERS………………………………….on page 40
UNIT 5: INTEGERS………………………………………………….on page 49
UNIT 6: ALGEBRAIC EXPRESSIONS………………………….on page 61
UNIT 7: UNITS OF MEASUREMENT…………………………on page 73
UNIT 8: PERCENTAGES AND PROPORTIONALITY…….on page 86
UNIT 9 AND 10: ANGLES, LINES, POLYGONS AND
CIRCUMFERENCES………………………………………………….on page 101
UNIT 11: AREAS AND PERIMETERS………………………….on page 117
UNIT 13: FUNCTIONS AND GRAPHS………………………..on page 128
2
UNIT 1
NATURAL NUMBERS
1. DECIMAL NUMBER SYSTEM
In our decimal number system, the value of each digit depends on its place
in the number. Each place is 10 times the value of the next place to its
right.
hundreds
tens
units
0
thousands
tens of
thousands
hundreds of
thousands
millions
Tens of
millions
Hundreds of
millions
Millions of
millions
7
2
3
1
5
5
9
7
4
5
8
2
3
6
5
5
5
7
How read and write numbers.
How many units, tens, hundreds,… does a number have?
985: You write or read: “Nine hundred eighty-five”.
985 = 900 + 80 +5 The number has nine hundreds, eight tens,
five units.
1725 = 1000 + 700 + 20+ 5 The number has one thousand, seven hundreds,
two tens, five units.
The number is “one thousand seven hundred twenty-five”.
3
25435 = 20000 + 5000 + 400 + 30 + 5 The number has two tens of
thousands, five thousands, four hundreds, three tens, five units.
The number is “twenty-five thousand four hundred thirty-five”.
7035567 = 7000000 + 30000 + 5000 + 500 + 60 + 7 The number has seven
millions, three tens of thousands, five thousands, five hundreds, six tens,
seven units.
The number is “seven million thirty-five thousand five hundred sixtyseven”.
Exercise 1:
Find as many numbers as you can and write them below:
T
W
O
Y
T
F
I
F
H
U
N
D
R
E
D
O
R
T
E
L
E
V
E
N
E
Y
T
F
O
U
R
T
E
T
S
I
X
V
T
W
H
N
E
V
O
E
A
E
S
E
V
E
N
T
Y
L
I
W
E
I
G
H
T
V
T
T
N
O
R
E
Z
E
Two = 2
Exercise 2:
Write these numbers with words
146 ....................................................................................................................................................................
17 .......................................................................................................................................................................
4
269 ....................................................................................................................................................................
292 ....................................................................................................................................................................
353 ....................................................................................................................................................................
310 ....................................................................................................................................................................
48 ......................................................................................................................................................................
434 ....................................................................................................................................................................
705 ....................................................................................................................................................................
661 ....................................................................................................................................................................
2358 .................................................................................................................................................................
1653 ..................................................................................................................................................................
3842 .................................................................................................................................................................
4986 .................................................................................................................................................................
5531 ..................................................................................................................................................................
6934 .................................................................................................................................................................
9537 .................................................................................................................................................................
8302 .................................................................................................................................................................
6980 .................................................................................................................................................................
7045 .................................................................................................................................................................
87......................................................................................................................................................
139 .................................................................................................................................................
4021 .............................................................................................................................................
........................................................................................................................................................
5
31435 ...........................................................................................................................................
.......................................................................................................................................................
128907 .........................................................................................................................................
......................................................................................................................................................
8010735 .....................................................................................................................................
.....................................................................................................................................................
Exercise 3:
How many units, tens, hundreds and thousands do the following numbers have?
For example: 25 contains 5 units and 2 tens.
a) 356 =........................................................................................................................
b) 138 = .....................................................................................................................
c) 2.405 = ................................................................................................................
d) 3.745 =................................................................................................................
e) 7.010 =.................................................................................................................
f) 99 = .....................................................................................................................
Exercise 4:
Match each sentence in column A to one number in column B.
For example: 1 – f
A
1)
2)
3)
4)
5)
6)
7)
B
One hundred, forty-eight
Thirteen thousand and forty-eight
Three million, forty-five thousand and forty-eight
Thirty-five
Thirteen million, forty-five thousand and forty-eight
Three hundred and forty-five thousand and forty-eight
Two thousand and seven
6
a) 2.007
b) 13.048
c) 35
d) 345.048
e) 13.045.048
f) 148
g) 3.045.048
2.FUNDAMENTAL ARITHMETIC OPERATIONS
a + b you can say:
“the sum of a and b” ;
“a plus b” ;
“a increased by b”;
“b more than a”;
or
“add b to a”
a –b you can say:
“The difference of a and b” ;
“a minus b”;
“a less b”;
“a decreased by b”;
“b subtracted from a” or
“take away b from a”
a · b you can say:
“the product of a and b” ;
“a times b”
or
“a multiplied by b”
Commutative property a · b = b · a
a + b= b + a
Distributive property a ·(b + c) = a ·b + a ·c
Associate property (a · b) · c = a ·(b ·c)
(a + b) + c = a + (b + c)
7
Dividend
10
Divisor
:
5
Division sign
=
a : b we can say:
“the quotient of a and b”
“a divided by b”
or
“b goes into a”
Quotient
2
We say: “ten divided by five equals two”
3 POWERS AND ROOTS
POWER WITH NATURAL BASE AND NATURAL INDEX
• A power is an abbreviated form to express a multiplication whose factors
are all equal.
• The base of a power is the factor that is repeated and the index is the
number of times that this factor is repeated.
• The value of a power is the product of multiplying the base as many times
as the index indicates.
• The value of an exponent of 10 is equal to one followed as many zeroes as
the index indicates:
8
Properties
*
The power of a product is the product of the powers of the factors:
*
The power of a quotient is equal to the quotient of the power of initial dividend and
the initial divisor:
*
To multiply powers with the same base, we keep the base and we add the indices:
*
To divide powers with the same base, we keep the base and we subtract the indices:
*
To raise powers with the same base, we keep the base and we multiply the indices:
*
Every power with a base other than zero and with an index of zero is equal to one:
*
Every power with an index of one has the value of the base:
we say “five squared”
we say “three to the fifth power” or “three to the power of five”
SQUARE ROOTS
To calculate the square root of a number “a” is look for another number “b”
that, when squared, gives “a”
= the radical sign , a = the radicand, b= the value of the root
9
3. COMBINED OPERATIONS
To calculate the value of an expression that includes different
types of operations we have to complete it in the following order:
1. We calculate the value of the parentheses if there are any
(brackets/square brackets).
2. We calculate the value of the powers or roots
3. We multiply and divide from left to right.
4. We add and subtract from left to right.
Exercise 5:
Operate with natural numbers:
Exercise 6:
Copy each calculation and put brackets in to give the answer shown
10
Exercise 7:
Helen goes to the swimming - pool three days a week. Every day she swims
1300 meters. How many meters does she swim in four weeks?
Exercise 8:
In a supermarket there are 15 boxes of milk with 12 bottles each. A bottle
has two liters. How many liters of milk are there?
Exercise 9:
Peter buys 3 CDs for 18 € each and 2 books for 15 € each. He pays with a
100 € bill. How much money does he get back?
Exercise 10:
A van delivers 179 crates of cola. There are 24 bottles in a crate.
How many bottles are there altogether?
11
Exercise 11:
A coach carries 56 passengers. How many coaches are needed to carry
1624 people?
Exercise 12:
A company has 197 boxes to move by van. The van can carry 23 boxes at a
time. How many trips must the van make to move all the boxes?
Exercise 13:
The same van does 34 kilometers to the liter of petrol. Each trip above is
31 kilometers. Can the van deliver all the boxes if it has 8 liters of petrol in
its tank?
12
Exercise 14:
Every day 17 Jumbo jets fly from London to San Francisco. Each jet can
carry up to 348 passengers. How many people can travel from London to
San Francisco every day?
Exercise 15:
On a farm, 547 eggs are collected and put into cartons of one dozen. How
many cartons are filled? How many eggs are left over?
Exercise 16:
A butcher sells 58 kilos of beef at €13 per kilo and 63 kilos of pork at €7
per kilo. How much money does he get in total?
13
UNIT 2
divisibility
1.
MULTIPLES
The multiples of a number are its products with the natural numbers 1,2, 3, …;
they are the numbers in its multiplication table.
Properties:
a) A natural number, a, is multiple of itself and of the unit because a · 1 =a
b) A natural number, a, a ≠ 0, has infinite multiples because natural numbers
are infinite.
c) Zero is a multiple of every natural number because a x 0 = 0
d) The multiples of a number are obtained by multiplying the number by each
of the natural numbers.
Exercise 1:
What are the first five multiples of
a)4?....................................................................................
b)12?..................................................................................
c)20?..................................................................................
Exercise 2:
Write down the first ten multiples of 5
Exercise 3:
Write down all the multiples of 6 between 20 and 70
14
Exercise 4:
Write down all the multiples of 7 between 30 and 80
Exercise 5:
Write the three smallest multiples of 8 which are greater than 50
Exercise 6:
Write the smallest multiple of 37 which is greater than 500
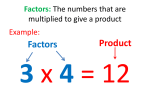
2. FACTORS
A natural number, a, is a factor of another number, b, if the division of b by a is
exact.
If a natural number can be expressed as a product of two natural numbers, then
these numbers are called factors of that number.
For example, 14 = 2 · 7 , so 2 and 7 are factors of 14
All the factors of a number are obtained by dividing this number by 1,2,3,4,… until
the quotient is equal or less than the divisor.
For example, 12 has six factors: 1,2,3,4,6 and 12.
15
Exercise 7:
List all the factors of
a) 20
b)42
c) 60 d) 100
PRIME NUMBERS: Numbers that are not divisible by any other number than one
and itself.
DIVISIBILITY RULES: Shortcuts to determine when a number can be divided by
certain other numbers.
Numbers are divisible:
By two: all even numbers (the number end in 0, 2, 4, 6 or 8)
By three: The sum of its digits is divisible by three.
By five: The number ends in zero or five
For example:
a) 54 is divisible by 2 and 3.
b) 30 is divisible by 2,3 and 5
By seven: There isn’t a rule to determine if a number is divisible by 7. You need to
divide.
By eleven: If the sum of the digits in the even position minus the sum of the digits
in the odd position is 0 or divisible by eleven.
Exercise 8:
Which of these numbers 14, 20, 22, 35, 50, 55, 70, 77, 99,250, 293, 765, 570,
495, 6402, 2088 are multiples of:
a) 2? ……………………………………………………………………………………………………………….
16
b) 3? ………………………………………………………………………………………………………………..
c) 5? ………………………………………………………………………………………………………………..
d) 7? …………………………………………………………………………………………………………………
e)11?..................................................................................
Exercise 9: Do you know who Eratosthenes was?
He was a mathematician of Ancient Greece (276-195 BC). He
discovered a method to determine if a number is a prime number or not. It was
called THE SIEVE OF ERATOSTHENES
We start with a table of natural numbers from 1 to 100 and cross out the number
1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
a) Circle the number 2 and then cross out all the multiples of 2.
b) Circle the number 3 and then cross out all the multiples of 3.
c) Circle the number 5 and then cross out all the multiples of 5.
17
d) Continue this process until there is no number to be crossed.
e) Make a list of all the circled numbers.
Exercise 10:
Complete the next table with “YES” or “NO”, if the following numbers are divisible
by 2, 3, 5, 6, 7, 10 or 11.
Div 2
Div 3 Div 5 Div 6
Div 7
Div 10
Div 11
92
113
2325
137
150
193
5.321
438
420
46
1.298
Exercise 11:
Change the letters for digits that the following numbers can be divided by 3:
a) 56A
b) 8B0
c) C5431
Exercise 12:
Change the letters by digits that
a) 451 and 4B5 can be divided by 3
18
d) 401D58
b) 827C and 29D0 can be divided by 5.
c) 4E57 and 4FF4 can be divided by 2.
Exercise 13:
Match each number in column A with a sentence in column B
A
B
1) 45
a) is a prime number
2) 41
b) is divisible by 13
3) 15
c) is multiple of 9
4) 52
d) is a factor of 45
Exercise 14:
Find out all the multiples of 7 that they are between 500 and 600.
Exercise 15:
Write the following numbers as a product of prime numbers: 60, 49, 128, 175 and
1024 .
19
60
49
128
175
576
60=
49=
128=
175=
576=
3. COMMON MULTIPLES
Common multiples are multiples that are common to two or more numbers.
For example:
The multiples of 6 are 6,12,18,24,30,36,42,48,54,60,…
The multiples of 9 are 9,18,27,36,45,54,63,72,81,…
18 and 36 are multiples of both 6 and 9, therefore 18 and 36 are common multiples.
LOWEST/LEAST COMMON MULTIPLES (LCM)
The lowest common multiples (LCM) of two or more numbers is the smallest
common multiple
For example: LCM(6,9) = 18
To calculate the LCM of two or more numbers follow the steps:
1) Break down (factorise) the numbers in prime numbers.
2) Find the common prime factors with the highest exponent and the non common
factors.
3) Multiply these factors.
20
GREATEST/HIGHEST COMMON FACTOR (GCF or HCF)
The biggest number that is a common factor of two or more numbers.
For example: Find the GCF of 30 and 18
The factors of 30 are: 1, 2, 3, 5, 6, 10, 15, 30
The factors of 18 are: 1, 2, 3, 6, 9, 18
Common factors are 1, 2, 3, 6.
6 is the greatest common factor.
To calculate the H C F of two or more numbers follow the steps:
1) Break down (factorise) the numbers in prime numbers.
2) Find the common prime factors with the lowest exponent.
3) Multiply these factors.
Exercise 16:
Find a number which is a common multiple of:
a) 2 and 6 …………………………………………………….
b) 7 and 5 …………………………………………………….
c) 2 and 3 and 7 ……………………………………………
d) 4 and 5 and 9 …………………………………………..
Exercise 17:
I am a factor of 24. I am an odd number. I am bigger than 1. What number am I?
Exercise 18:
I am a factor of 30. I am an even number. I am less than 5. What number am I?
21
Exercise 19:
What is the biggest number that is a common factor of 42 and 18?
Exercise 20:
What is the smallest number that has both 4 and 18 as factors?
Exercise 21:
Work out the Highest Common Factor and the Lowest Common Multiple of the
following numbers:
a) 40 and 60
b) 35 and 90
c) 180 and 198
d) 20 , 50 and 120
Exercise 22:
Ms. Rose wants to decorate her garden. She has a rectangle – shaped
garden. She wants to plant trees on every side and she wants them to
be the same distance from each other. If the long sides of her garden are
each 24 m long and the short sides each 18 m long, what is the lowest
number of trees she should plant?
22
Exercise 23:
Mr. and Mrs. White are moving into a new house. They want to have their
bathroom floor tiled. The bathroom is rectangle shaped and has sides 4.6 m
x 6 m. What’s the size of the biggest square- shaped tile (in centimeters)
that we can use? (don’t forget he can’t cut the tiles and there is no space
without tiles)
Exercise 24:
Mr. Bracket works in a factory with his two sons. He takes a break every
140 minutes. His sons take breaks in 210 minutes and 280 minutes. How
many minutes will they have to wait after their first break together to
meet again?
Exercise 25:
John is playing with bricks. He wants to build a cube with them. If his
bricks have dimensions 10 cm, 20 cm and 25 cm, what’s the volume of the
smallest cube (in cm3) he can build?
23
Exercise 26:
Mrs. Bell owns a small grocery store. She received 3 sacks of
sugar weighing 27 kg, 36 kg and 72 kg and she wants to put them
in equal-sized bags. What’s the least number of bags she needs if she
doesn´t want any sugar to be left without a bag?
Exercise 27:
Mrs. Flynn has baked 84 raisin cookies, 106 muffins and 128 chocolate chip
cookies. She wants to keep 4 raisin cookies, 6 muffins and 8 chocolate chip
cookies. She wants to put the rest into boxes with equal numbers of each type.
What is the largest number of cookies or muffins in each box?
Exercise 28:
Mrs. Stephens baked a fruit cake shaped like a rectangular prism with dimensions
6 cm, 8 cm and 10 cm. She wants to cut the cake into equal sized cubes. What’s
the least number of cubes she can make so that no part of the cake remains?
24
Exercise 29:
Ms. Pearl is shopping at the supermarket. She wants to make
hamburgers. She sees that hamburger buns come in packs of 8 but
the hamburgers are in packs of 10. What’s the least number of packs
she needs to get of each so that there are no leftovers?
Exercise 30:
We have 36 Kg of lemons and 54 Kg of oranges. We want to put them in similar
bags, with a natural number of Kg. Which is the highest possible number of Kg per
bag?
Exercise 31:
Ann and Peter visit together their grandparents on the 8th of April. Then, Ann
visits them every 15 days; Peter visits them every 9 days. When will Ann and Peter
visit their grandparents again together?
25
Divisibility Test
1) 18, 24 and 30 are all multiples of three
True
2) 5 is a multiple of 20.
False
True
3) Which list is made up of multiples of 4?
1, 4, 40
True
False
4, 14, 24
5) Six has all the following factors
1, 2, 3, 6
4) The multiples of 5 all end in 0 or 5
8, 16, 36
12, 22, 28
False
6) Five has only two factors.
3, 6, 12, 18 2, 4, 6
7) The factors of 24 include:
True
False
8) 12, 24 and 42 are all multiples of 6.
1, 6, 9
1, 8, 12
1, 5, 12
15, 30, 48
9) 62 is a multiple of 8
True
False
10) Which list is made up of multiples of 7?
True
False
11) The sixth multiple of nine is:
14, 25, 35
19, 26, 33
21, 35, 52
7, 14, 70
12) The factors of 28 are:
45
15
7, 14, 21
1, 6, 28
69
54
2, 4, 7, 14
1, 2, 4, 7, 14, 28
13) The factors of 35 are:
14) Seven is a factor of:
1, 3, 5, 35
5, 15, 20, 35
14, 27 and 72
21, 28 and 42
1, 5, 7, 35
1, 2, 4, 7, 35
1, 7 and 14
37, 47 and 57
15) 45, 63 and 70 are all multiples of 7.
True
False
17) 49 is a prime number.
True
16) 54 is a multiple of both 8 and 9.
True
False
18) The factors of 36 include
False
12, 15, 36
1, 6, 36
2, 4, 8
19) 9 is a factor of:
1, 13, 18
20) The Highest Common Factor of 2 and 3 is.
1, 3 and 9
9 and 49
45 and 54
28 and 82
6
26
1
0
UNIT 3
FRACTIONS
KEYWORDS
Fraction
Quantity
Numerator
Proper
Top number
fraction
Denominator
Improper
Bottom
fraction
number
Mixed
Part
of
a number
whole
Equivalent
fractions
To simplify
To cancel
Cancellation
Lowest terms
Simplest form
Common
denominator
Reciprocal
1. FRACTIONS
You use a fraction to describe a part of a
whole. A natural number divided by another
natural number. The division symbol is a
fraction bar (---) or sometimes a slash ( / ).
In any fraction, the “top number” is called the
numerator and the “bottom number” is called the denominator. The denominator
of a fraction cannot be zero. (Division by zero is undefined.) The denominator tells
us how many equal parts the whole is divided into and the numerator tells us how
many of these parts there are.
How do you read fractions?
You can see fractions in shops, on bills, in newspapers and recipes. It's a good idea
to recognise fractions when they are written as words.
27
fraction
word
plural
1
2
One (a) half
halves
1
3
One third
thirds
1
4
One quarter or a fourth
quarters or fourths
1
5
One fifth
fifths
1
6
One sixth
sixths
1
7
One seventh
sevenths
1
8
One eighth
eighths
1
9
One ninth
ninths
1
10
One tenth
tenths
It's easy to make the words, apart from the first four. All the other fractions
are like the numbers but with a 'th' sound added at the end.
Even easier is making the plurals, as long as you are careful with the plural of 1 .
2
Just put an 's' on the end of the other fractions
Here are some more examples of fractions in words.
Words
Figures
Words
Figures
two fifths
2
5
three eighths
3
8
four fifths
4
5
two thirds
2
3
28
Can you see how it works? The first number goes on the top, the second number on
the bottom.
If the number in the denominator is greater than 10 you have two forms to read
the fraction:
.
A fraction is a proper fraction if the numerator is smaller than the denominator.
The fraction represents a number less than one.
Example: 5/9 (five ninths)
A fraction is an improper fraction if the numerator is larger than the
denominator. The fraction represents a number greater than one.
Example: 15/2 (fifteen halves)
If the numerator is equal to the denominator, the fraction is equal to one.
An improper fraction can be convert to a mixed number (a natural number
followed by a proper fraction) dividing the numerator by the denominator, the
quotient is the natural number, the remainder is the new numerator and the
denominator is the same.
Example:
(four and one fifth)
To convert a mixed number to an improper fraction: Multiply the natural number
by the denominator. Add the numerator. This is the new numerator. Keep the same
denominator.
2. EQUIVALENT FRACTIONS
Two fractions are equivalent if they have the same value.
Examples:
;
;
HOW DO YOU OBTAIN EQUIVALENT FRACTIONS?
29
1.- Reduce or simplify a fraction: Divide numerator and denominator by a common
factor.
Example:
(we divide the numerator and the denominator by 2)
2.- Simplify to lowest terms: Reduce a fraction so the numerator and the
denominator have no common factors, dividing by the highest common factor
(Irreducible fraction)
Example:
3.- Amplify a fraction: Multiply numerator and denominator by the same number.
Example:
4.-Reduce to common denominator: Change the fractions to equivalent fractions
with the same denominators.
a) Chose a common multiple to use as common denominator.
b) If you use the L.C.M. then you work with the smallest numbers.
c) Find equivalent fractions with this denominator.
Exercise 1:
Calculate an equivalent amplified fraction and another equivalent simplified
fraction of the following:
Exercise 2:
Copy and complete:
30
Exercise 3:
Reduce to common denominator the following fractions:
3. COMPARING FRACTIONS
HOW DO YOU ORDER FRACTIONS?
1.- Fractions with the same numerator: If two fractions have the same
numerator, the bigger fraction is the one with the smallest denominator.
Example:
2.-Fractions with the same denominator: If two fractions have the same
denominator, the bigger fraction is the one with the biggest numerator.
Example:
3.-Fractions with different numerators and denominators: You have to reduce the
fractions to common denominator.
Exercise 4:
Copy and complete with the sign < or >.
31
Exercise 5:
Put the following fractions in increasing order:
4. OPERATIONS WITH FRACTIONS
ADDITION AND SUBTRACTION:
1.-To add or subtract fractions with the same denominators, add or subtract the
numerators and keep the denominators.
Examples:
You must change mixed numbers to improper fractions before you add or
subtract.
2.-To add or subtract fractions with different denominators, rewrite the
fractions as equivalent fractions with common denominators. Then follow the rule
for addition and subtraction of fractions with the same denominators.
Examples:
We use the L.C.M. of the
denominators
32
MULTIPLICATION:
Multiply the numerators and multiply the denominators. You must change mixed
numbers to improper fractions before you multiply.
Examples:
YOU MUST
SIMPLIFY !!!!
c)
DIVISION:
Multiply by the RECIPROCAL (the inverted form) of the divisor. Mixed numbers
must be changed to improper fractions before they can be inverted.
Examples:
(Cross multiply)
Exercise 6:
Calculate and simplify the following operations:
33
Exercise 7:
Calculate and reduce:
1
3
a) +
1 1
2 5
b)
1 1 1
- +
2 3 4
c)
3 1
- +1
4 2
d) 3 -
1 2
+
2 3
e)
1
1
+26
3
f) 2 -
1 1
+
3 2
Exercise 8:
Operate with fractions:
2 1
+
3 6
b) 3 -
1 1
+
2 3
d)
a) 2 -
2
1
+ 3 -
3
4
3 1 2 1
- - +
2 4 3 2
c) 3 -
34
Exercise 9:
Calculate and reduce:
3 1 1 1
: + :
2 2 3 2
1 1 1
- +
2 3 4
b)
a) 2 :
c)
2
1 2
+3: ·
3
4 3
5. A FRACTION OF AN AMOUNT
To calculate the fraction of an amount (a number) you divide the number by the
denominator and multiply the result by the numerator.
Example:
Exercise 10:
Calculate the following fractions of amounts:
a) 2/3 of 15
b) 3/4 of 80
c) 3/20 of 400
e) 2/7 of 21
h) 3/5 of 75
f) 3/5 of 80
g) 5/4 of 16
Exercise 11:
If Paul ran
miles each day last week, how many miles did he run?
35
d) 1/3 of 60
Exercise 12:
Mary studied
an hour on Monday and
an hour on Tuesday. How
much more did Mary study on Tuesday?
Exercise 13:
Peter wants to lose 10 kilograms. After two months he has lost of this amount. How
much weight has he lost?
Exercise 14:
Pat uses
cups of sugar to make a pie. How many pies can be made from
15 cups of sugar?
Exercise 15:
On Friday, it snowed
inches and on Saturday it snowed
total snowfall for the two days?
36
inches. What was the
Exercise 16:
Which is greater; the product of
or the quotient of
?
Exercise 17:
Jane spent 4/5 of her pocket money on a DVD player. Her sister spent 10/15
of her pocket money on clothing. Did they spend the same portion of their
money?
Exercise 18:
Mike is 133 cm tall. If he is as tall as Jim, how tall is Jim?
Exercise 19:
What fraction of a day is 3 hours? How many minutes are in
an hour?
37
5
of
6
Exercise 20:
Carlos spends 3 hours on homework each night. He spends ¼ of his time on Math,
1/3 on Social Studies, 1/6 on Science and 2/8 on English Language. Which two
subjects does he spend an equal amount of time working on? How much time does
Carlos spend working on each subject?
Exercise 21:
Twenty minutes before the school play, 4/9 of the auditorium was full. Ten
minutes later, 7/8 of the auditorium seats were occupied. What fraction of the
people arrived during those 10 minutes?
Exercise 22:
Henry made nine apple pies and five chocolate pies for the school
festival. What fraction of the pies were apple pies?
Exercise 23:
If students spend 10 months in school, then what fraction of the
year are students off?
38
Exercise 24:
1
of her chocolate bar and
2
2
Jesse gave Abbey
of his piece. What fraction
3
Sam gave Jesse
of the original chocolate bar did Abbey get?
Exercise 25:
Jeremy gave
1
of his candy bar to 4 friends. If his
2
friends shared the piece equally, then what fraction
of the original candy bar did
each one get?
Exercise 26:
Justin gave
2
of his pizza to 4 friends who shared the pizza
3
equally. What fraction of the original pizza did each one get?
39
Across 5. Write
as a mixed number
7. When adding fractions with ________ denominators, you must find the least common
denominator
8. Reduce
to lowest terms
11. Equivalent fractions have the ________ value but different names
12. Reducing a fraction to lowest terms in _________step requires dividing its numerator and
denominator by the greatest common factor
13. When comparing fractions with the same denominator, you only have to compare the ________
14. Reduce
to lowest terms
15. What is the reciprocal of ?
16. When adding or subtracting fractions, we ________ add or subtract denominators
Down
1. To find an equivalent fraction for a certain fraction, you could _________ its numerator and
denominator by the same number
2. Write 2 as an improper fraction
3. The numerator of an improper fraction is ________ than its denominator
4. Mixed numbers have a _________ number part and a fraction part
5. The least common denominator of 15 and 20
6. and
are _________ fractions
7. If a fraction is not in lowest terms you could ________ its numerator and denominator by the
same number to get an equivalent fraction
9.
and are equivalent fractions. What is the value of x?
10. Any whole number could be written as a fraction with a _________ of one
40
UNIT 4
DECIMAL NUMBERS
1. DECIMAL NUMBERS
The DECIMAL SYSTEM is based on the number 10. In this system, numbers
with DIGITS to the right of the one’s place are called decimal numbers. The
digits to the right of the one’s place are called decimals. The whole number
portion is separated from the decimals by a decimal point.
A decimal number has two parts:
As with whole numbers, a digit in a decimal number has a
value which depends on the place of the digit. The places to the left of the
decimal point are ones (units), tens, hundreds, and so on, just as with whole
numbers. This table shows the decimal place value for various positions:
Note that adding extra zeros to the right of the last decimal digit does not
change the value of the decimal number.
Place (underlined)
1.234567
1.234567
1.234567
1.234567
1.234567
1.234567
1.234567
Name of Position
Ones (units) position
Tenths
Hundredths
Thousandths
Ten- thousandths
Hundred - thousandths
Millionths
Example:
In the number 5.6734, the 5 is in the units place, the 6 is in the tenths place, the
7 is in the hundredths place, the 3 is in the thousandths place and the 4 is in the
ten-thousandths place.
41
Reading Decimal Numbers:
There are two forms to read them:
a)The digits to the left of the decimal point are read as whole numbers, the
decimal point is read as “and”, and the digits of the decimal portion are read
as a whole number followed by the name of the decimal place value furthest
to the right.
b) We have to read the whole number, then the word “point” and the decimal
numbers one by one.
Examples:
a) 1.23 is read as “one and 23 hundredths” or “one point two, three”
b) 15.236 is read as “fifteen and two hundred and thirty-six
thousandths” or fifteen point two three six”
c) 0.0025 is read as “25 ten-thousandths” or “point, zero, zero, two,
five”
Exercise 1:
Write in words the following decimals:
a) 0.42 _________________________________________________
b) 0.016_________________________________________________
c) 5.3___________________________________________________
d) 1.05__________________________________________________
e) 12.408________________________________________________
f) 42.5__________________________________________________
g) 216.73________________________________________________
h) 3.5908________________________________________________
i) 85.642 ________________________________________________
42
Exercise 2:
Write with digits the following decimals:
a)Twenty-five hundredths
b) Forty-two thousandths
c) Three units and nine hundredths
d) Twenty ones and five hundred and thirteen thousandths
e) Two ones and ninety-three thousandths
f) Ten units and three thousandths
2. COMPARING DECIMAL NUMBERS
To compare two decimals:
1) We compare the whole number part (look to the left of the decimal point)
2) If the whole part is the same, we add zeroes onto the decimal part of one
number until they both have the same amount of decimal numbers, then we
compare the decimal numbers
For example: 5.7 > 5.286, because 700 is greater than 286
Exercise 3:
Put this numbers in order from least to greatest: 5.9; 6.6 ; 6; 6.1; 5.4
Exercise 4:
Put this numbers in order from greatest to least: 3.03; 3.17; 3.3; 2.98; 3.1
Exercise 5:
Write four numbers between 7.25 and 7.26
43
3. OPERATIONS
Addition and Subtraction
Organize the numbers so that one is under the other one and the decimal point
are in the same column. Then proceed like with whole numbers. (Column method for
addition and subtraction) When one number has more decimal places than other,
complete with zeros to give them the same number of decimal places.
Examples:
a) 15.84 + 4.7 + 0.628
b) 23.84 – 5.726
Exercise 6:
a) Add 4.35 and 0.4
b) Add 15.23 and 2
c) Subtract 5.93 from 7.04
d) Subtract 5 from 16.25
e) Add 4.53 and 0.45
f) Subtract 3.8 from 6
44
Multiplication:
Multiply the numbers without paying attention to the decimals. The sum of the decimal places
is the number of decimal places in the product.
Examples:
a) 4.5 x 1.2 = 45 x 12 (2 decimal places) = 540 (2 decimal places) = 5.40
b) 0.003 x 0.0001 = 3 x 1 (7 decimal places) = 3 (7 decimal places)= 0.0000003
Exercise 7:
a) 42.6 · 5.9
b) 24.8 · 0.05
c) 765.3 · 3.8
d) 6.54 · 0.7
Multiplying a decimal number by a multiple of ten
To multiply a decimal number by 10, 100, 1000, …, the decimal point is moved to
the right one, two, three or more places, the same number of places as there are
zeroes.
Exercise 8:
a) 42.6 · 10
b) 24.8 · 1,000
c) 765.3 · 100
d) 6.543 · 10,000
e) 0.237 · 100
f) 1.36 · 1000
Division
The divisor is made into a whole number by moving the decimal point to the right.
Move the decimal point in the dividend the same number of places. Mark the
decimal point and continue with the division of whole numbers. Then when you
bring down the first decimal you must put the decimal point in the quotient and
continue with the division.
45
Exercise 9:
a) 4.5 : 3
b) 5.13 : 0.3
c) 14.25 : 0.05
d) 73.456 : 1.25
Dividing a decimal number by a multiple of ten
To divide a decimal number by 10, 100, 1000, …, (it’s the same as to multiply by 0.1,
0.01, 0.001,…)the decimal point is moved to the left one, two, three or more
places, the same number of places as there are zeroes.
Exercise 10:
a) 8.7 :100
b) 214: 10000
c) 534.3 · 0.001
d) 32.45 · 0.01
Exercise 11:
Five swimmers are competing. Four swimmers have finished their turns. Their
scores are 9.8 s, 9.75 s, 9.79 s and 9.81 s. What score
must the last swimmer get in order to win the
competition?
(s = seconds)
Exercise 12:
Helen wants to buy the following items: a DVD player for 49.95 €, a music
CD for 19.95 € and a book for 21.95 €. Does Helen have enough
money to buy all these items if she has 90 € with her?
46
Exercise 13:
Melissa spent 39.46 € for groceries at a store. The cashier gave her 1.46 €
change from a 50 € bill. Melissa gave the cashier an angry look. What did
the cashier do wrong? How much change should Melissa get from the cashier?
Exercise 14:
Printing one page costs 0.008 €.
a) Find out how much it costs to print a book with 85 pages.
b) What is the difference in costs for printing a 120-page
book and a 100-page book?
Exercise 15:
Jack bought 8 drill bits for 1.22 € each, ten washers for 0.11 € each, and
two hammers for 4.59 €.
a) Estimate his total bill.
b) What was his change from 50 €?
47
Exercise 16:
a) Your old fridge uses 984 kWh of energy per year. If you
pay 0.093 € per kWh, what is the cost of electricity for
running that fridge?
b) A new fridge will only use 407 kWh per year. How much
money will you save yearly, if you switch to that fridge?
Exercise 17:
A glass contains 225 ml. An adult needs about 1.8 liters of water each
day to stay healthy. How many glasses is that?
Exercise 18:
Marcela bought two and a half meters of fabric to make a dress. If a meter
of fabric cost €12.85, how much did she spend?
Exercise 19:
John buys a melon that weighs one and a half kilos at the market. He also
buys a loaf of bread that weighs four hundred and fifty grams and a fish
that weighs 1.235 kg. What is the total weight of his purchases?
48
Exercise 20:
Marta had five euro and bought a notebook that cost three
euro and eighty-five cents. How much money did she have
left?
Exercise 21:
A driver stops in a petrol station and fills his car up with
petrol. How many euros does he need to pay if the pump
register says he has used 42.6 litres of petrol and each
litre costs 95 cents?
Exercise 22:
Andrea weighs 72.4 kilos and goes on a diet in order to lose 1.250 kilos every
month. How many does she hope to weigh in six months?
Exercise 23:
Francisco goes forward 0.8 meters with each step he takes. How many steps
does he take if he covers a distance of 40 meters?
49
UNIT 5
integER numbers
KEYWORDS
Integer
minus
greater than
absolute value
opposite
Bellow
compare
above
1. NEGATIVE NUMBERS
We need to express values that are below zero in many situations in real life …
then we use negative numbers. For example:
a) Describing temperature: -4°C is a temperature of 4°C below zero.
b) Storing food: These ice-creams must be stored below -20°C to stay frozen.
c) Describing depths or levels: In a building -2 is the second floor underground.
d) Owing money: I have red numbers in my bank account.
2. INTEGER NUMBERS
INTEGER NUMBERS is the set of the natural numbers, zero and the opposite
(negative) of the natural numbers.
{…, -3, -2, -1, 0, 1, 2, 3, …}
The number line goes on forever in both directions. This is indicated by arrows.
* Whole numbers greater than zero are called positive integers. These numbers
are to the right of zero on the number line.
50
* Whole numbers less than zero are called negative integers. These numbers are
to the left of zero on the number line.
*The integer zero is neutral. It is neither positive nor negative.
*The sign of an integer is either positive (+) or negative (-), except zero, which
has no sign. Positive integers can be written with or without a sign.
* Two integers are opposites if they are each the same distance away from zero,
but on opposite sides of the number line. One will have a positive sign, the other a
negative sign. In the number line below, +3 and -3 are labelled as opposites.
Exercise 1:
Write an integer to represent each description:
a) 14 units to the right on a number line.
b) 8 units to the left on a number line.
c) A loss of 3 000 euro.
d) It`s very cold outside. The temperature is nine degrees below zero.
e) Deposit 1 707 euro into a bank account.
f) 12 grades above zero.
g) Marta owes six euro.
h) The car is parked on level one of the underground car park.
i) My team lost three points today.
j) Fifty-two feet below the sea level.
k) The opposite of 56.
l) Win at the lottery an amount of £150.
m) I made a loss of £2000 on the deal.
51
n) Susan deposits £300 in her bank account.
o) John withdraws £150 from his bank account.
p) The temperature goes up 5°C.
q) The temperature goes down 3°C.
r) Richard owes £150 to his father.
s) I live on the second floor.
t) The lift goes down three floors.
Absolute value
Problem:
Jill and Juan were at Amy’s house. Jill rode her bicycle 3 miles west of Amy’s
house, and Juan rode his bicycle 3 miles east of Amy’s house. Who traveled a
greater distance from Amy’s house, Jill or Juan?
Solution: Jill and Juan both traveled the same distance from Amy’s house since
each traveled 3 miles (in opposite directions).
The problem above can be solved using integers. Travelling 3 miles west can be
represented by -3. Traveling 3 miles east can be represented by +3. Amy’s house
can be represented by the integer 0.
The integers +3 and -3 are opposites. They are each 3 units from zero.
ABSOLUTE VALUE is the size of a number, it`s its distance from zero on the
number line. It has no sign before it and is always positive. The absolute value of
+3 is 3, and the absolute value of -3 is 3. Opposite integers have the same
absolute value.
|+3| = 3 ;
; |-5| = 5
52
Exercise 2:
Find the absolute value of the numbers +11,-9,+14,-10,+17,-19,+20,-20.
Exercise 3:
How many values of x will you get when you solve
= 20?
Compare and order integers
To compare integer numbers you can represent them on the number line, the
integer on the right is greater than the integer on the left.
Exercise 4:
Represent these integers on the number line and put them in order from least
to greatest.
-1, 6, 5, -5, -8, 19, -13, -7.
Exercise 5:
Put the integers in order from least to greatest:
a) 59, -13, 43, -26, -62, 34, 16:
b) -22, 7, 8, -3, -4, 19,-8, 14, 3, 18, 12:
3. OPERATIONS WITH INTEGERS
Addition of two integers
A) When you add integers with equal signs, add the absolute values. The sign of
the sum is the sign of the numbers added.
For example: (+5) +(+3) = +8 ; (-4) + (-6) = -10
53
b) When the signs are different, find the difference between the absolute values.
The sign of the answer is the sign of the number with the largest absolute value.
For example: (-4) + (+5) = +1 ; (+6) + (-9) = -3
Subtraction of two integers
When you subtract integers, change the sign of the second integer, then add
Examples:
a) 4 - (+5) = 4 + (-5) = 4 – 5 = -1
b) -3 – (+7) = -3 + (-7) = -10
c) 5 – (-6) = 5 + 6 = 11
d) -7 – (-3) = -7 + 3 = -4
Integer addition and integer subtraction can be easier if you know the rules for
removing brackets.
If there is a ‘plus’ sign before a
bracket, the sign of the numbers
inside the brackets hold the same.
Examples:
3 + (−5) = 3 − 5 = −2
;
−7 + (+9) = −7 + 9 = 2
If there is a ‘minus’ sign before a bracket,
the sign of the numbers inside the brackets
is changed from ‘plus’ to ‘minus’ and from
‘minus’ to ‘plus’.
Examples: −7 − (+9) = −7 − 9 = −16
;
3 − (−5) = 3 + 5 = 8
Exercise 6:
Compute:
a) (−24) + (−8) =
b) (+14) + (−6) =
c) (+51) + (+7) =
d) (+9) + (−23) =
e) (+9) + (+17) =
f) (−32) + (−9) =
g) (−24) − (−8) =
h) (+14) − (−6) =
i) (+51) − (+7) =
j) (+9) − (−23) =
k) (+9) − (+17) =
l) (−32) − (−9) =
54
Exercise 7:
Calculate:
a) (-34) + (-44) =
b) 26 – (-48) =
c) 15 + (-23) =
d) (-38) – (-10) =
e) (-26) – (+2) =
f) (-34) + 48 =
g) 40 – (-16) =
h) (-14) – (+11) =
Exercise 8:
Remove brackets and compute.
a) 11 − (−6 + 3) =
b) 13 + (−8 + 2) =
c) 8 + (−8 + 8) =
d) (2 − 10) + [5 − (8 + 2)] =
e) [8 − (6 + 4)] − (5 − 7) =
f) (12 − 3) – [1 + (2 − 6)] =
Multiplication (division) of two integers:
STEP 1: Multiply (divide) the absolute value of the two numbers.
STEP 2: a) If the sign are the same, the sign of the product (quotient) is positive.
b) If the sign are different, the sign of the product (quotient) is
negative.
Examples:
a) (-2) · (-5) = 10
e) (+18) : (-3) = -6
b) (-3) · (+3) = -9
f) (-25) : (-5) = 5
c) (+4) · (-5)= -20
g) (-36) : (+9) = -4
d) (+2) · (+3) =6
h) (+50) : (+10) = 5
55
Exercise 9:
Complete:
a) (-4) · 41=
b) 8 · 33 =
c) (-6)· (-22) =
d) 49 · (-5) =
e) 3 · (−2) =
f) (−5) · (+3)
g) −2 · (−4) =
h) (+2) · (+6) =
i) (−3) · (−9) =
j) (+3) · (−8) =
k) (−8) : (+2) =
l) (+20) : (−5) =
m) (−12) : (−4) =
n) (+54) : (+6) =
o) (−6) : (+6) =
p) (+20) : (−10) =
Exercise 10:
Fill in the gaps:
a) (−6) · ___ = −18
b) (+60) : ___ = −5
c) (−7) · ___ = 35
d) ___ : (+6) = −12
e) ___· (−5) = −45
f) ___ : (−3) = 27
The order of operations with
integer numbers is:
1. Brackets. ( ) before [ ]
2. Division or Multiplication (left to
right)
3. Addition or Subtraction (left to
Exercise 11:
right)
Calculate:
a) 19 − (−3) · [5 − (+8)] =
b) 12 + (−5) ·[8 + (−9)] =
56
c) 12 – [13 − (−7)] : (−5) =
d) 10 − (+20) : [7 + (−3)] =
e) (−2) · (5 − 7) − (−3)·(8 − 6) =
f) (9 − 6)·(−2) + (13 + 3):(+4)=
Exercise 12:
A fish is 10 meters below the surface of the water. A fish
eagle is 15 m above the water. How many meters must the bird descend to
get the fish?
Exercise 13:
Alf has 25 euro in the bank. He writes a check for 35 €. How much has he
got in the bank now?
Exercise 14:
In a magic square, the numbers in any row, column or diagonal add up to give
the same answer. Complete:
-7
0
-8
-2
-3
-2
-4
-3
-8
57
0
-7
-12
-13
-5
-9
-3
-10
-15
Exercise 15:
Mount Everest, the highest elevation in Asia, is 29 028 feet above sea level.
The Dead Sea, the lowest elevation, is 1 312 feet below sea level. What is
the difference between these two elevations? (FEET: It is a unit of
measurement in the British System 3.2808 feet = 1 meter)
Exercise 16:
In Buffalo, New York, the temperature was -14 ºF (Fahrenheit)
in the morning. If the temperature dropped 7º F, what is the
temperature now?
FAHRENHEIT: It is a unit of temperature usually used in the UK
and USA
32
o
Fahrenheit = 0 o Celsius
Exercise 17:
A submarine is situated 800 feet below sea level. If it ascends 250 feet,
what is its new position?
58
Exercise 18:
Roman Civilization began in 509 B. C. and ended in 476
A.C. How many years did Roman Civilization last? (B.C. =
before Christ; A.C. = After Christ)
Exercise 19:
A submarine is situated 450 feet below sea level. If it descends 300 feet,
what is its new position?
Exercise 20:
In the Sahara desert one day it is 136º F. In the Gobi desert a temperature
of -50º F is recorded. What is the difference between these two
temperatures?
Exercise 21:
The Punic Wars began in 264 B. C. and ended in 146 B.C. How long did the
Punic Wars last?
THE PUNIC WARS: The Punic Wars were a series of three wars between
Rome and Carthage for control of the Mediterranean Sea.
59
Exercise 22:
I had 254 € in my bank account and I paid a bill of 386 €. How much money
have I got now?
Exercise 23:
Alicia owes £6 to each of 4 friends. How much money does she owe?
Exercise 24:
Alexander the Great was born in 356 BC and died in 323 BC. For
how many years did he live? How many years ago did he die?
Exercise 25:
Find the final temperatures in these science experiments:
a) Starting temperature 55°C. It goes up 32°, then down 100°.
b) Starting temperature -15°C. It goes down 28°, increases by 75° and then
it goes down 17°.
Exercise 26:
Find the balance in these bank accounts after the transactions shown:
a) Opening balance £133.45. Deposits of £45.55 and £63.99, followed by
withdrawals of £17.50 and £220.
b) Opening balance is -£459.77. Deposit of £6.50, followed by a withdrawal
of £17.85.
60
WORD SCRAMBLE
Integer numbers
a) Integer numbers can be represented on a ______ ____. (2 words)
b) Whole numbers greater than zero are called ________ integers.
c) The ________ value of an integer is its distance from zero on the
number line.
d) The ________ of the number (+3) is (-3).
e) The symbol < means ____ ____. (2 words)
f) As you move to the _____ on the number line, integer numbers get
larger in value.
g) If there is a ____ sign before a bracket, the sign of the numbers inside
the brackets hold the same.
h) The product of a positive integer and a negative integer is a
________ integer.
61
UNIT 6
ALGEBRAIC EXPRESSIONS
1. ALGEBRAIC EXPRESSIONS
A variable is a symbol that represents a number. We usually use letters such as x,
n, p, t for variables.
Letters are useful if we want to operate with an unknown number instead with a
particular one. Let us look at some examples:
We say that “s” represents the side of a square, then “s” represents a number
and:
4s is the perimeter of the square
s × s is the area of the square
When letters express numbers they have the same operating properties.
The part of mathematics that deals with the study of the expressions with
letters and numbers is called algebra.
An algebraic expression is a mathematical sentence that includes numbers and
letters.
Exercise 1:
Write the algebraic expression for these:
a)Three more than x …………………………
b) Seven less than y …………………..
c) Four multiplied by x ………………………
d) y multiplied by y ……………………..
e) Ten divided by b …………………………...
f) A number add five ……………………
g)The sum of x and 10……………………….
h)The difference between 123 and x….
i)The double of x………………………………..
j) The triple of x plus three units……….
k)The half of x minus seven…………….l)The three quarters of x plus forty-six…
62
Exercise 2:
Steven is 16 years old. How old will he be in:
a) 5 years? …………………… b) 10 years? ………………
c) x years? ……………………….
Exercise 3:
Tickets for a football match cost 25€ each. What is the cost for:
a) 2 tickets? ………………… b) 6 tickets? ………………. c) y tickets? ……………………….
Exercise 4:
There are n books in a pile. Write an expression for the number of books in a
pile that has:
a) 3 more books …………… b) 4 fewer books ………….c) Twice as many books …………
Exercise 5:
a) A square has sides of length 3 cm. What is its perimeter?
……………………………….. What is its area?..............................................
b) A square has sides of length d cm. What is its perimeter? ……………………………
What is its area? ………………………………………………
Evaluate an algebraic expression
Find the value of an algebraic expression by replacing each variable for a given
number.
63
Exercise 6:
Evaluate each algebraic expression using the values given:
2. MONOMIALS
The simplest algebraic expressions formed by products of numbers and letters
are called monomials.
A monomial consists of the product of a known number (coefficient) by one or
several letters with exponents that must be constant and positive whole numbers
(literal part).
Generally in the monomials the product signs are not included, so we find a number
followed by one or more letters, we understand that they are multiplied.
The degree of a monomial is the sum of the indexes of the variables.
Examples:
a) 2x is a monomial. 2 is the coefficient, x is literal part and the degree is 1.
b) − 3x2 is a monomial, -3 is the coefficient, x2 is the literal part, x is the variable
and the degree is 2.
64
c)
is a monomial,
is the coefficient, t7 is the literal part, t is the variable and
the degree is 7.
d) 5xy2 is a monomial, 5 is the coefficient, xy2 is the literal part, x and y are the
variables and the degree is 3.
e) 2x + 7 is an algebraic expression but it is not a monomial.
f) is an algebraic expression but it is not a monomial.
Exercise 7:
Find which of the following expressions are monomials and determine, if they
are so, their coefficient, literal part, variables and degree:
a)
b) 2t2
c) a + b
d) a9
e)
n3
f) 3
g) 7abc2
Simplifying algebraic expressions (adding and subtracting
monomials)
In many algebraic expressions we look for ways of simplifying the expression so
that it appears in the most compact form.
The first step in many such simplifications is to collect like terms.
The terms in an algebraic expression are the parts that are separated by + and –
signs.
5a + 3c + 2d – 7a ; It has four terms: 5a ; 3c ; 2d , 7a
The terms which have exactly the same letters in them are called “like terms” or
“like monomials”
65
7xy-3x+2xy+4x-5y
Like terms are 7xy and 2xy.
3x and 4x are like terms.
Collecting like terms means to bring them together as a single term. When the
literal parts are different the addition is left indicated.
This expression can be simplified as follows: 9xy+x-5y
Another example: 5x2-2x+7x2 is equal to 12x2-2x
To multiply two monomials we multiply the coefficients and also the literal parts
(remember how we multiply powers with the same base)
Exercise 8:
Simplify each algebraic expression:
a) -3p+6p
b) b-3+6-2b
c) 7x-x+4x
d) -10v+6v
e)9+5r-9r
f)10x+36-38x-47
g)-2(7-n)+4
h)-4p-(1-6p)
i) 7(k-8)+2k
j) 4+5b+5(1-3b)
k) 7x+13x-5x
l) -33v-49v
2. EQUATIONS
A formula is a method of expressing a rule by the use of symbols or letters.
An equation is a statement that two expressions are equal.
An equation has two equal sides or members: the left side and the right side.
When we solve equations, we find the value of the unknown or variable in relation
to other numbers in the equation.
66
To check the solution of equations, substitute the value of the unknown quantity
as determined in the answer for the corresponding symbol in the original equation.
If both sides produce the same answer, the answer is correct.
Example:
Check by substituting 10 in the equation
that 10 is the solution of
this equation.
Transposition is the process of moving a quantity from one side of an equation to
the other side by changing its sign of operation.
A term may be transposed from one side of an equation to the other if its sign is
changed from + to - , or – to +.
A factor or multiplier may be removed from one side of an equation by making it a
divisor in the other. A divisor may be removed from one side of an equation by
making it a factor in the other.
When terms involving the unknown quantity occur on both sides of the equation,
perform such transpositions as may be necessary to collect all the unknown terms
on one side (usually the left) and all the known terms on the other.
Exercise 9:
Solve the following equations and check the solutions:
a)
b)
c)
d)
e)
f)
g)
h) 2(x + 5)+ 1= 17
i) x - 22 = 13 – 4
j) 23 + y + 2y = 3
k) 3x − 5x = 23
l) 5x + 7x = 23 – 1
67
m) 44 + x = 12 − 3x
n) 3(x − 2) = 7
Exercise 10:
Write an equation for each and solve them.
1.- When 5 is subtracted from one fourth of a number, the result is 2.
2.- When 35 is subtracted from a number, the result is 62.
3.- When 500 is divided by a number, the result is 25.
4.- When 4 is added to 6 times a number, the sum is 52.
5.- One fifth of the difference of 30 and a number is 2.
6.- Five times a number is 75.
7.- The difference between 89 and a number is 38.
8.-When a number is divided by 4, the quotient is 16.
3. TRANSLATING WORD PROBLEMS INTO
EQUATIONS
Most of the time when someone says “word problems” there is automatic
panic. But word problems do not have to be the worst part of a math class.
68
Here are some recommended steps:
1. Read the problem carefully and identify what you have to find out.
2. Assign a variable (a letter) to the quantity you have to find out.
3. Write down what the variable represents.
4. Re-read the problem and write an equation for the quantities given in
the problem. (Sometimes a drawing is useful)
5. Solve the equation.
6. Answer the question in the problem.
7. Check your solution.
Exercise 11:
6 is added to four times a number, the result is 50. What is the number?
Exercise 12:
The sum of a number and 9 is multiplied by -2 and the answer is -8. What is
the number?
Exercise 13:
On an algebra test, the highest mark was 42 points higher than the lowest
mark. The sum of the two marks was 138. Find the lowest mark.
69
Exercise 14:
The length of a rectangular map is 15 centimeters and the perimeter is 50
centimeters. Find the width of the map.
Exercise 15:
If 4 is subtracted from twice a number, the result is 10 less than the
number. What is the number?
Exercise 16:
Karin’s mom runs a dairy farm. Last year Betty the cow gave 375 liters less
than twice the amount from Bessie the cow. Together, Betty and Bessie
produced 1464 liters of milk. How many liters did each cow give?
Exercise 17:
Twice a number is added to the number and the answer is 90. What is the
number?
70
Exercise 18:
Jose has a board that is 44 centimeters long. He wishes to cut it into two
pieces so that one piece will be 6 centimeters longer than the other. How long
should the shorter piece be?
Exercise 19:
The perimeter of a triangular lot is 73 meters. One side is 16 meters, and
the second side is twice the third side. Find the length of the other sides of
the triangular.
Exercise 20:
A man was asked how much he paid for his watch. He said:”If you multiply
the price by 4, and to the product add 70, and from this sum subtract 50,
the remainder will be equal to 220 dollars”. What is the price of his watch?
Exercise 21:
From the sum of a number and its half, 20 is subtracted. The result is a
fourth of the number. What is the number?
71
Exercise 22:
A father divides his money between his three sons, so that:
The first son get $1000 less than half of the whole;
The second son get $800 less than one third of the whole;
The third son get $600 less than one fourth of the whole;
How much money does the father have?
Exercise 23:
Divide 48 into two such parts, that if the less is divided by 4, and the
greater by 6, the sum of the quotients will be 9.
Exercise 24:
If to a certain number, 720 is added, and the sum is divided by 84; the
quotient will be equal to the number divided by 300. What is that number?
72
Exercise 25:
A man spent one third of his life in England, one fourth of it in Scotland, and
the remainder of it, which was 20 years, in the United States. How old was
he when he died?
Exercise 26:
We have 4 packets of eggs and 3 eggs.
In total we have 19 eggs.
The packets have an equal number of eggs. What is the number of eggs per packets?
Exercise 27:
We have 5 bags of sweets and 2 sweets. In total we have 42 sweets.
All bags have an equal number of sweets. What is the number of sweets per bag?
Exercise 28:
John spends one fourth of his money on going to the cinema, 5 euro on sandwiches and
he still has 3€. How much money did John have?
73
UNIT 7
Units of measurement
1. THE METRIC SYSTEM
The metric system, also known as the Système International d’Unités (SI), was
developed in the late 1700s to standardize units of measurement in Europe.
Different units of measurement have been used in the past, some of them are
still in use in the UK and USA, but in most places the Metric System of
Measurements is used.
The metric units are:
Length: metre (In U.S.A. “meter”)
Area: square metre
Volume: cubic metre
Capacity: litre (In U.S.A. “liter”)
Mass or weight: gram
The metric (decimal) system uses a number of standard prefixes for units of
length, mass, etc.
To change any of the other units of measurement into their equivalent
values in the main unit we have to use the conversion factor given by the
value of the prefix.
Number
10
100
1000
1,000,000
9
10
12
10
Prefix
deca
hecto
kilo
mega
giga
tera
Symbol
da
h
k
M
G
T
Number
0.1
0.01
0.001
0.000001
0.000000001
0.000000000001
Prefix
deci
centi
mili
micro
nano
pico
Symbol
d
c
m
µ
n
p
The simplicity of the metric system due to the fact that there is only one
unit of measurement (or base unit) for each type of quantity measured (length,
mass, etc.).
74
The three most common base units in the metric system are the metre, the gram,
and the litre. With these simple measurements we can measure nearly
everything in the world
For every step upward on the chart you are dividing by 10 or moving the
decimal point one place to the left.
When you move down the stairs you are multiplying by 10 for each step or
moving the decimal point one place to the right.
2. LENGTH
Length is a measurement of distance. You can measure how long things are, or how
tall, or how far apart they are. The main unit of length is the metre; their
multiples and factors are:
Kilometre(km),Hectometre(hm), Decametre(dam),
Metre(m),
Decimetr(dm), Centimetre(cm), Millimetre(mm)
Exercise 1:
Write all the following in centimetres.
a) 4 cm 2 mm
b) 18 cm 9 mm
75
c) 75 mm
d) 4 dm 3 cm 45 mm
e) 7.8 m 43 dm
f) 55.3 m
g) 0.3 dam 5 cm 64 mm
h) 0.05 hm 5 m 36 cm
i) 4.6 km 0.3 dam 0.5 m 78 mm
Exercise 2:
Write all the following in millimetres.
a) 0.4 cm 12 mm
b) 1.78 cm 15 mm
c) 17.5 m
d) 35 dm 13 cm 67 mm
e) 17.4 m 45 dm
f) 75.8 m
g) 0.7 dam 5 m 64 mm.
h) 1.05 hm 15 m 36 cm
i) 0.06 km 0.3 dam 1.6 m 38 dm
Exercise 3:
Write all the following in metres.
a) 10.4 cm 140 mm
b) 198 cm 150 mm
c) 17.5 km
d) 37 hm 13 m 1067 mm
e) 32.6 dam 470 dm
f) 1275.8 mm
g) 0.29 dam 5 m 765 mm
h) 1.32 hm 150 m 3600 cm
i) 0.005 km 0.12 dam 1.6 m 38 cm
Exercise 4:
Write all the following in kilometres.
a) 10700 cm 140000 mm
b) 158 m 120000 mm
c) 17.5 hm
d) 346 hm 14m 10400 mm
76
e) 320.9 dam 47000 dm
f) 1275.8 dam
g) 8.78 dam 500 m 775000 mm
h) 43.32 hm 150000 m
i) 0.005 km 14 dam 160 m 38000 cm
Exercise 5:
Round each of the following measurements to the nearest centimetre.
a) 3.84 cm
b) 158 m 1.2 mm
c) 415.5 mm
d) 134 m 19 mm
e) 342 dam 0.47 dm
f) 1273.8 mm
Exercise 6:
Give the most sensible unit for measuring the following lengths.
a) The width of a table.
b) The thickness of 10 sheet of paper on top of each other.
c) The length of football field.
d) The distance from one city to another.
e) The height of an adult person.
Exercise 7:
There are 35 English books in the pile on the teacher’s desk. If each book is
8 mm thick, what is the height of the pile in centimetres?
3. CAPACITY
Capacity is a measurement of the amount of liquid a 3-D shape contains. The main
unit of capacity is the litre; these are their multiples and factors.
Kilolitre(kl), Hectolitre(hl), Decalitre(dal) ,
Litre(l);
77
Decilitre(dl); Centilitre(cl); Millilitre(ml)
Exercise 8:
Write all the following in centilitres.
a) 14 cl 32 ml
b) 4 dl 3 cl 45 ml
c) 0.38 dal 5 cl 68 ml
Exercise 9:
Write all the following in litres.
a) 90.5 hl 5 l 36 cl
b) 15.6 kl 0.03 dal 3.6 l 668 ml
c) 4.2 kl 0.53 dal 0.5 l 780 ml
Exercise 10:
Write all the following in kilolitres.
a) 43107cl 670140000 ml
b) 73.39 hl 17000 l
Exercise 11:
Round each of the following measurements to the nearest litre.
a) 16.84 dl
b) 543 l 640 ml
c) 127 l 98 dl
d) 2283.5 ml
4. WEIGHT
Mass is a measurement of the amount of matter in an object. Mass is linked to
78
weight. The base unit for mass is the gram.The unit of weight is the gram
Kilogram(kg); Hectogram(hg); Decagram(dag);
Gram(g);
Decigram(dg); Centigram(cg); Milligram(mg)
1 ton (USA) (tonne (UK)) = 1000 kg
A tenth of a tonne = 100 kg
Exercise 12:
Find your own weight in all the units.
Exercise 13:
(You must be groups of four). Calculate the average weight of the group.
Round the result to the nearest
a) kg
b) hg
c) dag
Exercise 14:
The average weight of a group of ten boys is 72 kilograms 890 grams. When
one boy leaves the group the average of the nine becomes 72.5 kg.
Find the weight of the boy who left the group.
Exercise 15:
A bridge has been designed to support 550 tons. If the average weight of a
vehicle is 1 ton 850 kg, is it safe to have 300 vehicles on the bridge at one
time?
79
5. AREA
The area of a shape is the amount of space it covers.
The base unit for area is the square metre.
A square metre is the area of a square that is 1 m on each side. The SI unit of
area is the square meter. To change any of these other units of area into their
equivalent values in square meters use the operation given.
Square kilometer, square hectometer; square decameter; square meter;
Square decimeter; square centimeter; square millimeter
Land measurements units are: 1 a (Are) = 1 dam2=100 m2
1 ha (Hectare) = 1 hm2=10 000 m2
For every step upward on the chart you are dividing by 100 or moving the
decimal point two places to the left.
When you move down the stairs you are multiplying by 100 for each step or
moving the decimal point two places to the right.
Exercise 16:
Write all the following in m2.
a) 3 km2 5 hm2 54 dm2
b) 7,890 ha 23 a
c) 30,000 dm2
80
Exercise 17:
Write all the following in Ares and in hectares.
a) 90.5 km2 5 hm2 36 dam2
b) 1.6 dam2 0.03 km2 34500 dm2
c) 5,000,000 cm2
Exercise 18:
Give the most sensible unit for measuring the area of each of the following.
a) Portugal.
b) A house.
c) A sheet of paper.
d) A television screen.
e) A football pitch.
Exercise 19:
Copy and complete.
a) 5.1 km2 = ________ hm2
b) 825 hm2 = ________km2
c) 0.03 hm2 = ________m2
d) 12500 m2 = ________ha
e) 3500 ha = ________km2
f) 53000 m2 = ________ dam2
g) 420 cm2 = _________ mm2
h) 52800 mm2 = _______ dm2
i) 5 m2 4 dm2 7 cm2 = _________ m2
j) 5 km2 48 hm2 25 dam2 = ______ m2
6. VOLUME
The distinction between 'Volume' and 'Capacity' is artificial and kept here only
for historic reasons. Volume is the amount of space a 3-D shape or substance
occupies or contains.
The volume of a container is generally understood to be the capacity of the
container rather than the amount of space it occupies.
The base unit for volume is the cubic meter. One liter is the capacity of a cubic
decimeter.
81
A cubic metre is 1000 litres, a cubic decimetre is a litre, and a cubic
centimetre is a millilitre.
Exercise 20:
Write all the following in m3.
a) 0.0003 km3 0.05 hm3 5400 dm3
b) 7,320 dm3 5000 cm3
c) 210,000 dm3
Exercise 21:
Write all the following in cm3 and dm3
a) 0.0123 m3 40 dm3 45800 mm3
b) 0.0000045 dam3 0.323 m3 0.234 dm3
c) 5,000,000 mm3
7. VOLUME, MASS AND CAPACITY
One gram is the weight of 1 cm3 of pure water.
The following table shows the relationship between the different measurements.
Volume
Capacity
Mass
m3
kl
t
hl
q
dm3
l
kg
dal
mag
Exercise 22:
Write all the following in litres and in centilitres.
a) 0.0000125 hm3 5.4 dm3
b) 0.000043 hm3 50000 cm3
c) 210,000 millilitres
82
dl
hg
cl
dag
cm3
ml
g
Exercise 23:
Write all the following in cm3 and dm3
a) 10.7 kl 40 hl 44,300 l
b) 6.7 kl 234 cl
c) 5,000,000 ml
Exercise 24:
A recipe needs 550 grams of flour to make a cake. How many 1 kg bags of
flour you need to make six cakes?
Exercise 25:
A melon weighs 900 grams. A melon and an apple weigh 1.1 kilograms. How
many grams does the apple weigh?
8.IMPERIAL UNITS
IMPERIAL UNITS are the measurement units that were historically used in the
British Commonwealth countries.
Most people around the world use metric units but in Britain many people still use
imperial units.
83
The imperial units still commonly in use are:
Length
12 inches (in)=1 foot (ft)
3 feet = 1 yard (yd)
1760 yards= 1 mile
Mass
16 ounces (oz) = 1 pound (lb)
14 pounds = 1 stone (st)
Capacity
8 pints (pt) = 1 gallon
You need to know the metric equivalents of these measurements. The imperial
system was developed using practical measurements such as the length of a foot.
The metric system was developed using scientific measurements. So the
equivalents are not exact, just rough estimates.
Length
1 inch 2.5 cm
1 foot 30 cm
1 yard 90 cm
1 mile 1.6 km
1 km
mile
Mass
1 kg 2 lb
Capacity
1 pint
1 pint =568 ml
1 liter 1.75 pints
Equivalents
3 feet yard ; 5 miles 8 km
Exercise 26:
Complete this table of metric equivalents:
Imperial measurement
2 feet
6 feet
3 pints
1 gallon
25 yards
100 yards
10 miles
174 miles
liter
Metric unit
Centimeters
Metric equivalent
60 cm
Exercise 27:
Complete this table of imperial equivalents:
84
Metric measurement
4 kilograms
3 liters
150 centimeters
18 kilometers
279 kilometers
Imperial unit
Imperial equivalent
Exercise 28:
Measure your height in meters and centimeters. Convert your result to feet
and inches.
Exercise 29:
How many kilograms does your school bag weigh? How many pounds is this?
Exercise 30:
The supermarket sells strawberries for 2.50 € per kilogram. The corner shop
sells strawberries for 1.15 € per pound. Which is the cheapest?
Exercise 31:
1 pint of coke in a restaurant is 1.30 €. A 2 liter bottle costs 1.39 €.Which
is the best value?
85
MEASUREMENT CROSSWORD
ACROSS
1 Fuel is priced by the _________
4 A liquid is measured in a measuring ___
6 5 ml is a typical measurement for which: teaspoon / drinks can / milk
carton
10 A prefix meaning one thousand
12 Millilitre is abbreviated to _____
14 Four ______ is a typical length for a small car
15 Which is the shortest length: mm / cm / km
16 Standard length of a ruler in cm
17 An Olympic sprinter runs a _________ metres
DOWN
2 One kg is equal to one __________ g
3 Ten millilitres equal one
5 “g” is an abbreviation of _________
7 Weight of a bag of sugar
8
One thousand metres
9 “1,6 litres” refers to a car’s engine _________
11 “km” is a measurement of _________
13 The unit “kg” is used to measure which of the following: weight / length
86
UNIT 8
PERCENTAGES AND PROPORTIONALITY
1. FRACTION, DECIMAL AND
PERCENTAGE EQUIVALENTS
All these amounts show part of a whole:
PERCENT, or %, means a number of parts of one hundred. A
percentage is a fraction written as a number of parts per 100.
For example:
and
You should be able to convert between fractions, decimals and
percentages…
Using place value:
Cancelling factors:
Finding an equivalent fraction:
By dividing the numerator by the denominator of a fraction:
Once you change a fraction to a decimal you can easily convert it to a percentage.
You just multiply the decimal by 100.
CONVERTING PERCENTS TO DECIMAL OR FRACTIONS:
a) To change a percent to a decimal, remove the percent sign and move the decimal
point two places to the left.
Example 1: Change 25% to a decimal: 25% = 0.25
Example 2: change 1.5% to a decimal: 1.5% = 0.015 (You need to put zeros)
b) To change a percent to a fraction, divide the percent quantity by 100, and
reduce to lowest terms.
Example 3: Convert 8% to a fraction in lowest terms:
87
Example 4: Convert 75% to a fraction in lowest terms:
CONVERTING DECIMALS TO PERCENTS:
To change a decimal to a percent, move the decimal point two places to the right
and add a percent sign.
Example 5: Change 0.24 to a percent: 0.24 =24%
Example 6: Change 0.0043 to a percent: 0.0043 = 0.43%
Example 7: Change 2.45 to a percent: 2.45 =245%
Exercise 1:
Copy and complete this table:
Fraction
Decimal
0.7
0.45
Percentage
120%
32%
Exercise 2:
These are the marks which Rufus scored in each of his exams:
French:
German:
History:
Maths: 77%
English:
Geography: 72%
a) Convert all the marks to percentages.
b) In which subject did he do the best? Explain your answer.
c) Put the marks for each subject in order, starting with the lowest.
88
2. PERCENTAGES OF AMOUNTS
Look at this example:
There are 300 cars in a car park. 20% of the cars are red. How many cars
are red?
A percentage is a fraction out of 100.
20% means 20 parts per 100 (or 20 parts in every 100)
20% of 300 is the same as
.
Remember that you find fractions of a quantity by multiplying.
20% of 300 is
Therefore, there are 60 red cars in the car park.
You can calculate the percentage of an amount using mental methods, using an
equivalent fraction or using an equivalent decimal.
• Use mental methods to find simple percentages
Example: 50% of 400.
50% of a quantity is the same as one half of that quantity, so 50% of 400 are 200.
• Change the percentage to its equivalent fraction and multiply by the amount.
Example: 9% of 24 m.
9% of 24 m
• Change the percentage to its equivalent decimal and multiply by the amount.
Example: 37% of £58.
37% of £58 =
6
(0.37 is the decimal equivalent of 37%)
Exercise 3:
Calculate these, using a mental or written method as appropriate:
a) 15% of £27 b) 10% of 340 m c) 125% of 84 cm d) 25% of 160 kg
89
Exercise 4:
A suit is designed from a material containing 14% cotton. If the suit weighs
385 grams, what is the weight of cotton in the suit?
Exercise 5:
A mathematics textbook has 420 pages. 35% of the pages are on number,
30% are on algebra and the remainder pages are on shape.
How many pages are there on shape?
Exercise 6:
Three women ran for eight minutes around a track: Rachel ran
of 1500 m,
Mary ran 65% of 1 km and Monica ran 161% of 400 m.
a) How far did each woman run?
b) How far ahead of the last runner was the first runner?
3. PERCENTAGE PROBLEMS
The terms commonly used in percentage problems are p = percent ; C = total or
initial amount and A=the part. There are different types of percentage problems.
1) Find the percentage of a number or amount:
Example: Find 14% of 300€
14% = 0.14 ↔ 300€ X 0.14 = 42€
14% of 300€ is 42€
2) Find what percent one number is of another number:
Example: What percent of 240 is 120?
90
↔
Divide the part by the initial amount to get the rate.
Rewrite the answer,
, as the percent, 50%. So 120 is 50% of 240.
Using the formulae
3) Find the total or initial amount if the percent and the part are known:
Example: 225 is 25% of what amount?
In lowest terms:
Exercise 7:
a) Find 30% of 620 tables.
b) Find 12% of 125 men.
c) What is 4% of 250 pounds?
d) How much is 62% of 80€?
e) Find 15% of 190 grams.
f) What percent of 32€ is 8€?
g) What percent of 200€ is 14€?
h) Twelve is 25% of what number?
i) Ten is 20% of what number?
j) Eight is 2% of what number?
k) Sixteen percent of a number is 128. What is the number?
91
4. PERCENTAGE INCREASE AND
DECREASE
In real life, lots of things are increased or reduced by a percentage
You can add on a percentage increase or subtract a percentage decrease at
the end of the calculation.
Example 1:
A computer costing £540 is increased in price by 15 %. What is the new
price of the computer?
Original price = £540 ; Percentage increase = 15%
Increase = 15% of the original price = 15% of £540 = £81
New price = original price + increase = £540 + £81 = £621
Example 2:
A book costing £18 is reduced in a sale by 22%. What is the sale price?
Original price = £18 Percentage decrease = 22%
Reduction = 22% of the original price = 22% of £18 = £3.96
Sale price = original price - reduction = £18 - £3.96 = £14.04
Alternatively you can calculate the percentage increase or decrease in a single
calculation.
Example 1:
A computer costing £540 is increased in price by 15 %. What is the new
price of the computer?
New price = (100 + 15)% of original = 115% of £540 = 1.15 · £540 = £621
Example 2:
A book costing £18 is reduced in a sale by 22%. What is the sale price?
Sale price = (100 - 22)% of original = 78% of £18 = 0.78 · £18 = £14.04
Exercise 8:
What number increased by 25% of itself equals 120?
92
Exercise 9:
A loaded truck weighs 20,000 kilograms. If 80% of this represents the load,
how much does just the truck weigh?
Exercise 10:
A truck carrying 6,750 kilograms of coal weighs 9,000 kilograms. What
percent of the total weight is the weight of the truck?
Exercise 11:
A bronze statue with a tin base weighs 28 kilograms. If the base weighs
kilograms. What percent of the total weight is bronze?
Exercise 12:
In Gordon’s Health Club, 8% of the exercise machines broke down. How many
exercise machines are there altogether if 32 machines have to be repaired?
93
Exercise 13:
Gill used to weigh 72 kg. After going on a diet she has reduced her weight by
24%. What is her new weight?
Exercise 14:
A meal costs £28 plus a 12% service charge. How much is the bill?
Exercise 15:
A shirt is originally priced at £19, but during a sale it is reduced by 35%.
How much does the shirt cost now?
Exercise 16:
Use the clues to fill the cross-number puzzle in. Then use the puzzle to fill
in the missing numbers in the clues.
1
2
3
4
5
7
6
8
9
94
Across
Down
1 71% of 300
1 96% of ………
3 73% of 200
2 81% of ………
5 107% 0f 200
3 50% of 24
8 58% of …….
4 25% of 596
9 88% of 400
6 61% of 200
7 100% of 63
Exercise 17:
Jeremy scored 85% on his last math test, which had 40 questions. How many
questions did Jeremy get correct?
Exercise 18:
There are 150 students in a school. If 90% of them come to school on
Thursday, how many students are not in class that day?
Exercise 19:
In a recent election, 25% of 20,000 people voted to have a recycling program
in Smithtown. In Lawrenceville, 15% of 30,000 voters made the same choice.
In which town did more people choose recycling?
95
Exercise 20:
Brendan had dinner at Burger King. The cost for food and beverage was
10.16 €. If the tax was 5%, what was the total Brendan paid for dinner?
5. PROPORTION
A proportion compares the size of the part (or portion) to the size of the whole.
In a class of 30, 18 are girls and 12 are boys.
The proportion of girls is 18 out of 30.
The proportion of boys is 12 out of 30.
You can express a proportion as a fraction, a decimal or a percentage.
Proportion of girls↔
Proportion of boys ↔
Exercise 21:
In a bag of 20 marbles, 14 are green and the rest are blue.
What is the proportion of green marbles?
6. DIRECT PROPORTION
Suppose the price of a can of soup is £0.50. If a person wants to buy 12 cans of
soup, then he has to pay £6. If he wants to buy 24 cans of soup, he has to pay £12
and so on.
We can easily see that if the person buys more cans, he has to pay more or he has
to pay less if he buys less cans.
Number of cans
Total price
12
6
24
12
36
18
96
That is, as number of cans is increased total price also is increased; conversely, if
the number of cans is decreased total price also is decreased. In such situation,
we say that number of cans and price are directly related.
When an increase in one quantity means another quantity increases in the same
proportion, the quantities are in direct proportion.
In other words:
If x and y are in direct proportion, then the division of x and y will be constant.
In the above example, we see that:
↔ each ratio is the same
Hence, if we are dealing with quantities which are in direct proportion, then we
can use the follow rule:
Number of cans 12
36
Total price
6
18
In general:
Quantity 1
Quantity 2
a b
c d
or
Example:
With 8 gallons of petrol my car travels 248 miles. How far will it travel with
11 gallons of petrol?
Gallons
Miles
8
248
11
x
97
Exercise 22:
A distance of 8 km is represented by 15.2 cm on a map. How many cm will
represent 10 km?
Exercise 23:
A family spends 120 dollars per month for vegetables when the cost of
vegetables is 5 dollars per kg. How much amount must the family spend per
month, if the cost of vegetables goes up to 5.75 dollars per kg?
Exercise 24:
One evening the length of the shadow of a building's pillar of height 28 m is
42 m. What will be the length of the shadow of the building's tower of
height 36 m at that time?
Exercise 25:
The weight E of a man on earth's surface is directly proportional to his
weight M on mars. The constant of proportionality is 3, if a man weights 126
kg on earth, how much will he weigh on mars?
98
7. INVERSE PROPORTION
Suppose that 20 men build a house in 6 days. If men are increased to 30 then take
4 days to build the same house. If men become 40, they take 3 days to build the
house.
We can easily see that if the number of men is increased, the time taken to build
the house is decreased in the same proportion.
Number of men
Number of days
20
6
30
4
40
3
When an increase in one quantity means another quantity decreases in the same
proportion, the quantities are in inverse proportion.
If x and y are in inverse proportion, then the product of x and y will be
constant.
In the above example, we see that:
20 × 6 = 120 ; 30 × 4 = 120 ; 40 ×3 = 120
In general
If we are dealing with quantities which are in inverse proportion, then we can use
the follow rule:
Quantity 1
Quantity 2
a
c
b
d
Example:
The groceries in a home of 4 members are enough for 30 days. If a guest
comes and stays with them, how many days will the groceries last?
Members
Days
4
30
5
x
99
Exercise 26:
At the rate of 28 lines per page, a book has 300 pages. If the book has to
contain only 280 pages, how many lines should a page contain?
Exercise 27:
Maria cycles to her school at an average speed of 12 km/h. It takes her 20
minutes to reach the school. If she wants to reach her school in 15 minutes,
what should be her average speed?
Exercise 28:
Some people working at the rate of 6 hours a day can complete the work in
19.5 days. As they have received another contract, they want to finish this
work early. Now they start working 6.5 hours a day. In how many days will
they finish the work?
Exercise 29:
In an army camp, there is food for 8 weeks for 1200 people. After 3 weeks,
300 more soldiers joined the camp. For how many more weeks will the food
last?
100
Exercise 30:
It takes 4 men 6 hours to repair a road. How long will it take 7 men to do
the job if they work at the same rate?
Exercise 31:
A team of five people can paint a house in three hours. How long will it take
a team of just two people?
Exercise 32:
If two pencils cost €1.50, how many pencils can you buy with €9.00?
101
UNITs 9 and 10
ANGLES, LINES, POLYGONS AND
CIRCUNFERENCES
1. LINES, RAYS AND LINE SEGMENTS
A point is one of the basic terms in Geometry. We say that a point is a “dot” on a
piece of paper. We identify this point with a capital letter. A point has no length
or width.
A line is a “straight” line that we draw with a ruler on a piece of paper, a line has
no beginning or end point. Imagine it continuing indefinitely in both directions. We
can illustrate that by little arrows on both ends.
A ray has a beginning point but no end point. A ray is a line that begins at a
certain point and extends forever in one direction. The point where the ray begins
is known as its endpoint
A line segment is a portion of a line. A line segment does not extend forever, but
has two different endpoints. We write the name of a line segment with endpoints
A and B as
Classification of lines
The term “intersect” is used when lines, rays or segments share a common point.
The point they share is called the point of intersection.
Two different lines could be classified as:
Intersecting lines: Two lines that intersect at the same
point.
Example: Line AB and line GH intersect at point D
Parallel lines: Two lines that
never intersect.
Example: Lines 1 and 2 are parallel.
Perpendicular lines: Two lines that intersect at right
angles (90º).
Coinciding lines: Two lines that intersect at all their points
2. ANGLES
102
In mathematics an angle is made up from two rays that have the same beginning
point. That point is called the vertex and the two rays are called the sides of the
angle.
The most common unit used when measuring angles is the degree.
Follow these easy steps when using a protractor to measure angles:
1) Place the centre of the protractor on the angle's vertex.
2) Rotate the protractor so that the straight
edge is placed over one of the angle's sides.
3) Use the scale that begins with zero. Read
where the other side of the angle crosses this
scale.
Angles can be classified based on their
measure:
An acute angle measures between 0 and 90 degrees.
A right angle measures 90 degrees.
An obtuse angle measures between 90 and 180 degrees.
A straight angle measures 180 degrees.
103
Exercise 1:
Mark the angles as acute, right, obtuse or straight.
Exercise 2:
Measure the size of the following angles using a protractor:
3. RELATED ANGLES
Complementary angles
Two angles are called complementary angles if the sum of their degree
measurements equals 90 degrees. One of the complementary angles is the
complement of the other.
For example 60º and 30º are complementary.
104
Supplementary angles
Two angles are called supplementary angles if the sum of their degree
measurements equals 180 degrees. One of the supplementary angles is the
supplement of the other.
For example 50º and 130º are supplementary.
Opposite angles
When two lines intersect, the opposite angles are equal.
On parallel lines, alternate angles are equal
Exercise 3:
Find the unknown angles:
a=
b=
c=
d=
e=
f=
g=
h=
i=
j=
k=
l=
m=
n=
105
Exercise 4:
Find the unknown angles:
1. a=
b=
c=
2. a=
b=
c=
3. a=
b=
c=
d=
4. a=
b=
c=
d=
5. a=
b=
c=
d=
6. a=
b=
c=
d=
e=
4. OPERATIONS WITH ANGLES
f=
The subunits of the degree are the minute of arc and the second of arc.
One minute
of a degree, that is 1º = 60 ’
One second
of a minute, that is 1 ‘ = 60’’
106
These are the sexagesimal units, so an angle “a” can be expressed for example
a = 25º 23’ 40’’ and we need to operate angles expressed in this form.
Addition
We need to add separately degrees, minutes and seconds and then convert the
seconds into minutes and the minutes into degrees if we get more than 60
subunits.
Example
Add 45º 53’ 40’’ +12º 33’ 35’’
Adding separately we get 45º 53’ 40’’ +12º 33’ 35’’ = 57º 86’ 75’’ but
75’’ = 1’ 15’’ so we add 1’ and get 87’ = 1º 27’ we add 1º and finally the solution is
57º 86’ 75’’ = 58º 27’ 15’’
Subtraction
We need to subtract separately degrees minutes and seconds, if we do not have
enough seconds or minutes we convert one degree into minutes or a minute into
seconds.
Example
Subtract 57º 13’ 21’’ and 12º 43’ 35’’ We write 57º 13’ 21’’ as 56º 73’ 21’’ and then:
Multiplication by a whole number
We multiply separately degrees, minutes and seconds and then convert the
seconds into minutes and the minutes into degrees when we get more than 60
subunits.
Example
Multiply (22º 13’ 25’’)× 6
Solution: 133º 20’ 30’’
Exercise 5:
Add:
a) 28º 35’ 43” + 157º 54’ 21
b) 49º 55’ 17” + 11º 5’ 47”
107
c) 233º 5’ 59” + 79º 48’ 40”
Exercise 6:
a) Subtract 34º 32’ 12” – 11º 30’ 22”
b) Calculate the complement of 13º 45’ 12”
c) Calculate the supplement of 93º 30’
Exercise 7:
Given A = 22º 32’ 41” Calculate:
a) 2·A
b) 3·A
c) 5·A
5. ANGLES IN THE POLYGONS
A polygon is a 2D-shape bounded by segments
Triangle
A triangle is a three-sided polygon.
The sum of the angles of a triangle is 180 degrees.
a +b + c =180º
Quadrilateral
A quadrilateral is a four-sided polygon
The sum of the angles of any quadrilateral is 360º
a + b + c = 180º ; d + e + f = 180º
a + b + c + d + e + f = 360º
108
Polygon of n sides
The sum of the angles of a polygon with n sides, where n is 3 or more, is
(n − 2)×180º .
Regular Polygon
A regular polygon is a polygon whose sides are all the same length, and whose
angles are all the same.
As the sum of the angles of a polygon with n sides is (n − 2)×180º , each angle in a
regular polygon is
Exercise 8:
Complete the following table:
NAME
NUMBER OF
SIDES
SUM OF THE
INTERIOR
ANGLES
Triangle
Quadrilateral
Pentagon
Hexagon
Heptagon
Octagon
Nonagon
Decagon
Undecagon
Dodecagon
109
NAME OF
THE
REGULAR
POLYGON
INTERIOR
ANGLE
6. TRIANGLES
A triangle is a three-sided polygon. Sides of a polygon are also called edges.
Triangles can be classified either by sides or by angles.
By sides:
Equilateral Triangle
It is a triangle that has: Three equal sides. Three equal angles of 60
degrees.
Isosceles Triangle
It is a triangle that has:
Two sides of equal length.
Two equal angles
Scalene Triangle
It is a triangle that has:
Three sides of different lengths.
Three different angles
By angles:
Acute Triangle
It is a triangle that has three acute angles.
Obtuse Triangle
It is a triangle that has an obtuse angle
Right Triangle
It is a triangle that has a right angle.
The side opposite the right angle is called the
hypotenuse. The two sides that form the right angle
are called the legs or catheti.
110
Exercise 9:
Classify the following triangles by their sides and by their angles. Find the
asked angles of the triangles.
Triangle
By the sides
By the angles
ABC
DEF
HGI
JKL
MNO
YAZ
BCD
QPR
SUT
XVW
MKL
NPO
GEF
QSR
UTV
HIJ
calculate
=
111
7. THE PYTHAGOREAN THEOREM
In a right triangle the sum of the squares of the lengths of the legs or catheti
equals the square of the length of the hypotenuse.
This is known as the Pythagorean Theorem.
For the right triangle in the figure, the lengths of
the legs are a and b, and the hypotenuse has length
c. Using the Pythagorean
Theorem, we can write that
a2 + b2 = c2.
The acute angles of a right triangle are
complementary.
Exercise 10:
Find the value of the third side of the following right triangles ABC in which
A = 90º:
a) b = 7 cm, a = 9 cm.
b) b = 3 cm , c = 4 cm
c) a = 12 cm, c = 8.6 cm
d) a = 0.3 cm, c = 0.2 cm
8. QUADRILATERALS
A quadrilateral is a polygon with four sides. The four angles of any quadrilateral
add up to 360º.
These are the special quadrilaterals
Rectangle
All the angles are right angles.
Opposite sides are equal.
Diagonals have the same length and bisect each other in their
middle points
112
Square
All the angles are 90º
All the sides are equal in length
Diagonals have the same length and bisect each other at right angles
in the middle point.
Rhombus
All the sides have the same length.
Opposite sides are parallel.
Opposite angles are equal.
Diagonals bisect each other at right angles in the middle
point.
Parallelogram or rhomboid
Opposite sides are parallel and have the same length.
Opposite angles are equal.
Diagonals have the same length and bisect each other in the
middle point.
Trapezium (U.K.) or Trapezoid (U.S.A.)
One pair of sides is parallel. The two sides that are parallel are
called the bases of the trapezium.
In an isosceles trapezium the base angles are equal,
and so is the pair of non-parallel sides.
Trapezoid (U.K.) or Trapezium (U.S.A.)
Quadrilateral that has no parallel sides
Kite
It is a special type of trapezoid in which:
The adjacent sides are equal.
Diagonals intersect each other at right angles
Exercise 11:
One of the sides of a rectangle measures 4 cm and the diagonal 6 cm
a) Construct the rectangle.
b) Calculate the other side and the perimeter.
113
Exercise 12:
In a rectangle the length of its sides are 8.3 cm and 5.4 cm. Calculate the
length of its diagonal.
Exercise 13:
Construct a rhombus with diagonals 4 cm and 7 cm. Calculate the perimeter.
Exercise 14:
Calculate the perimeter of a square with a diagonal of 7.5 cm.
9. REGULAR POLYGONS
A regular polygon is a polygon in which all angles are equal and all sides have the
same length.
Others polygons are called irregular polygons
114
All the regular polygons can be circumscribed by a circle, this is called the
circumcircle, and it is a circle which contains all the vertices of the polygon.
The centre of this circle is called the circumcenter and it is the centre of the
regular polygon. The radius of this circle is also the radius of the polygon.
Apothem is the line drawn from the centre of the polygon perpendicular to a side.
Example:
In this hexagon
O is the centre
OP is the apothem
OQ is the radius
Central angle is the angle formed with two radiuses
drawn in two consecutive vertices
Exercise 15:
Calculate the apothem of this pentagon
115
10. CIRCLE AND CIRCUMFERENCE
A circumference is the collection of points in a plane that are all at the same
distance from a fixed point. The fixed point is called the centre. A circle is the
shape inside the circumference. (The circumference and all the internal points)
Elements in a circle
Radius is the distance from the centre to the edge. (Segment OP)
Diameter is the segment between two points of the circle that passes through the centre.
(Segment QR) The diameter is the double of the radius. The diameter divides the circumference
in two equal parts whose name is semi circumference.
Chord is a straight line between two points of the circumference. (Segment CD)
Arc is a part of the circumference of a circle. (Curve CD) Any chord divides a circumference in
two arcs.
Sector is the shape made by two radiuses (radii) of the circle. (OAB)
Segment is a shape made by a chord and an arc. (Curve CD and segment CD)
Tangent is a straight line that touches the circle at only one point. (TU)
A tangent of a circle is always perpendicular to a correspondent radius
Secant is a line that intersects two points of a circle. (SU)
Exercise 16:
116
Express in seconds:
a) 12º 21’ 30’’
b) 5º 25’ 23’’
Exercise 17:
Operate with angles:
a) (32º 39’ 48’’) + (45º 34’ 33’’)
b) (32º 41’ 40’’) + (15º 18’’)
c) (30º 40’) + (15’ 18’’) + (38º 45’’)
d) (62º 39’ 49’’) - (45º 34’ 33’’)
e) (70º12’ 40’’) – (15º18’)
f) (45º 30’ 49’’) - (12’57’’) - (56’’)
Exercise 18:
Given the angles
a) The sum of
c) The triple of
y
, find the value of the following angles:
b) The subtract of
d) The complementary of
e) The supplementary of
Exercise 19:
In a right triangle, the catheti measure 5 and 12 cm. How many centimeters does the
hypotenuse measure?
117
Exercise 20:
In a right triangle, one cathetus measures 7 cm and the hypotenuse measures 25 cm. How
many centimeters does the other cathetus measure?
Exercise 21:
Find the diagonal of a rectangle whose sides measure 3 cm and 4 cm.
Exercise 22:
Find the biggest diagonal of a rhombus whose side is 50 cm and the other diagonal is 28 cm.
118
UNIT 11
AREAS AND PERIMETERS
1. PERIMETER
The perimeter of a polygon is the sum of the length of its sides.
2. AREA
The area of a polygon is the number of square units contained in its interior.
NAME
PLANE SHAPE
AREA
SQUARE
RECTANGLE
PARALLELOGRAM
TRIANGLE
RHOMBUS
TRAPEZIUM OR
TRAPEZOID
REGULAR
POLYGON
(n sides)
119
PERIMETER
CIRCLE
CIRCULAR
SECTOR
ANNULUS
Exercise 1:
The perimeter of a rectangle is 70 cm. and the length of its base is 15 cm.
Find the height and the area of this rectangle.
Exercise 2:
Find the perimeter of a rectangle. Its height is 4 cm and its area is equal to
56 cm2.
Exercise 3:
The area of a square is equal to 36 cm2. Which is the length of its side?
120
Exercise 4:
Find the area of a trapezium with bases of 9 cm and 5 cm and a height of 4
cm.
Exercise 5:
Find the area of a triangle with a base of 20 cm. and a height of 15 cm.
Exercise 6:
Find the area of a square whose sides are 21 cm long.
Exercise 7:
Find the area of a circle with a radius of 8 cm.
121
Exercise 8:
Find the area of a rectangle with dimensions of 7 m and 11 m.
Exercise 9:
Find the area of a regular octagon with 15 cm sides and an 18 cm apothem.
Exercise 10:
Find the area and the perimeter of a rhombus whose diagonals are 9 cm and
12 cm.
Exercise 11:
Find the area of a parallelogram with a base of 8 m and a height of 5 m.
122
Exercise 12:
Find the area of a trapezium with bases of 1 m and 80 cm and a height of 60
cm.
Exercise 13:
Find the area and the perimeter of a semicircle with a diameter 0f 40 cm.
Exercise 14:
Un terreno tiene forma de rombo. Si las diagonales miden 180m y 90m, ¿cuál
debería ser el lado de un cuadrado de igual área?
Exercise 15:
Calculate the perimeter of trapezoid ACDE from the shape bellow, where
ABDE is a rhombus and BCD is an isosceles triangle:
123
Exercise 16:
Work out the perimeter and the area of the following shapes:
3. AREA OF A COMPOUND SHAPE
A compound shape is any shape made up from two or more basic shapes.
You find the total area by addition or subtraction of the areas of its parts.
124
Exercise 17:
Find the area of the following compound shapes:
a)
b)
Exercise 18:
Find the area of the following shadowed shapes:
125
Exercise 19:
Find the area of these trapeziums.
Exercise 20:
Find the area of the following figures.
126
Exercise 21:
In a rectangular-shaped plot of 40 meters long and 25 meters wide, we have
built a chalet with rectangular base of 17 meters long and 11 meters wide.
Find the area of the garden.
Exercise 22:
Find the area of the following compound figure:
Exercise 23:
Find the length of the circumference and the area of the circle with a
diameter of 10 cm.
127
Exercise 24:
Calculate the apothem and the area of a regular hexagon whose side is 2 cm.
Exercise 25:
Calculate the length of the arc and the area of the sector of a circle of 70º
and a radius of 2 cm.
Exercise 26:
The area a rectangle is 72 cm2. Its long sides are double the length of its
short sides. How long is a short side?
Exercise 27:
Find the area of an equilateral triangle with each side measuring 3 cm.
128
UNIT 13
FUNCTIONS and graphs
1.THE COORDINATE GRID
Numbers can be represented on a line in this way
1. Draw a line.
2. Choose a point for zero.
3. Positive numbers are drawn to the right, negatives to the left.
Decimal numbers can also be placed on the line
Example: Place approximately on the number line the following numbers
a) 1.5
b) 2.8
c) - 5.3
d) - 3.7
How to plot points on a plane
To represent points in a plane we use two perpendicular number lines.
In the sixteenth century, the French mathematician René Descartes developed a
grid of numbers to describe the location of any point in the plane.
In the diagram below we have a horizontal line and a vertical one meeting at the
point 0. It is called the coordinate plane (or grid) or the Cartesian Plane in
honour of Descartes:
The horizontal line is called the x-axis (positives numbers to the right and
negatives to the left).
The vertical line is called the y-axis (positive numbers up and negatives down).
The common point of the two lines is called the origin O
For plotting a point we need an ordered pair of numbers, be careful! The order in
which the couple is written is important.
The first number of the pair is the x-coordinate (abscissa).
The second one is the y-coordinate (ordinate).
129
Let’s plot for example the point (2, 1): starting at the origin, we move 2 units to
the right along the x-axis; then move vertically up 1 unit. We describe the location
of this point as the ordered pair (2, 1).
Example : Plot the numbers A(-2,-3) B(5,-7) and C(-4,4) and D(5,-3.5)
The diagram below shows that the x-axis and the y-axis divide the plane into four
quarters. Each of these is called a quadrant:
130
Exercise 1:
a) Write the coordinates of A, B, C, D, E, F, and G
b) Which two points have the same x-coordinate?
c) Which two points have the same y-coordinate?
d) Which points have the same x and y coordinates?
e) Plot a point P which has the same x coordinate as C and the same y
coordinate as A.
f) Plot a point, which has the same coordinates as B but in the opposite
order.
g) In which quadrant is each point situated?
Exercise 2:
a) Plot the points A(-2,-2); B(0,0); C(4,4) and D(5.5,5.5).
b) Draw the line that joins all of them.
c) Plot P(5,7) and P’(7,5). What can you see?
d) Plot Q(-2,4) and Q’(4,-2). What can you see?
The points P’ and Q’ are the images of the points P and Q under reflection of
the symmetric line drawn in b).
e) Plot the points R(-4,-1) and the symmetric R’
f) Plot the points S(5,2) and the symmetric S’
131
Exercise 3:
Draw a grid. Join these points in the order they appear.
1. (2,2); (2,10); (9,10); (9,2); (2,2)
2. (3,7); (3,8); (4,8); (4,7); (3,7)
3. (7,7); (7,8); (8,8); (8,7); (7,7)
4. (5,5); (5,7); (6,7); (6,5); (5,5)
5. (4,3); (4,4); (7,4); (7,3); (4,3)
132
Exercise 4:
Write the coordinates of the points that are plotted on the Cartesian
diagram.
133
Exercise 5:
For each plotting draw a new coordinate diagram
1 Plot the points, join them in order and name the shapes
a) (2,2); (2,5); (6,5); (6,2); (2,2)
b) (2,6); (4,4); (7,7); (2,6)
2 Write down the coordinates of the missing point and name the shape.
(1,2); (2,5); (5,4); ( , )
3 Write down the coordinates of the missing points the shape is ABCDEFGH
its opposite angles are the same, but the sides are not all of the same
length.
A(0,0); B(-2,2); C(-2,4); D(0,6); E(3,6)...
2. GRAPH OF A FUNCTION
Graphs describe relationships between two different quantities; from this
relationship we can build up a set of pairs and draw a graph.
134
Example
Tomatoes are sold at €1.5 per kg, we can plot a graph showing the
cost depending on the number of kg bought like this:
You can see that all the points are on a line
These magnitudes are directly proportional, when one doubles the second will be
doubled also.
In general graphs describe the relationship between two variables x and y
x is the independent variable (in the example kg of tomatoes).
y is the dependent variable (in the example price of the purchase).
We see that y depends on x
Notice that for each x-value, there is one and only one possible y-value. This is
important!
Sometimes it is easy to describe the relationship by a formula in the example
the formula is y = 1.5·x
Exercise 6:
In the graph data is plotted about the height and weight of a group of
students, where x is the height in cm and y is the weight in kg of each one.
Answer these questions.
a) Who is the tallest and how tall is she/he.
b) Who is the heaviest and what is his/her weight.
c) How much heavier is Antonio than Alex?
d) Who are taller than Vanessa and who are shorter?
e) In this case, is it true that the taller people are generally heavier?
135
Exercise 7:
The graph below describes the time required to defrost a piece of meat in a
microwave oven depending of the weight.
1. How long is needed to defrost pieces of meat of:
a) 200g
b) 600g
c) 0.5 kg
d) 300 g
e) 1kg and 200g
2. What mass of meat can be defrosted in: a) 8min b) 15min
c) 1/2h
3. How much longer it takes to defrost 300g than 350g of meat?
136
Exercise 8:
This is the height of Wendy recorded every year since she was 4
a) How tall was Wendy at 7?
b) How old was she when she reached 132 cm?
c) Between which years she grow faster?
137
Exercise 9:
The distance from Paul’s house to the school is on the graph.
Describe his way to school.
a) What variables are associated?
b) What scale is used for each
variable?
c) How far is the school from
Paul`s house?
d) How much time does Paul
spend on going to the school?
Exercise 10:
Use this graph to answer the questions:
a) In which year were 75,000 cans of cola
drunk?
b) How many cans of cola were drunk in
1940?
c) How many cans of cola were drunk in
1970?
d) In which year were 45,000 cans of cola
drunk?
138