* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Chapter 1 Number Sets and Properties
Abuse of notation wikipedia , lookup
History of mathematical notation wikipedia , lookup
Foundations of mathematics wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
List of important publications in mathematics wikipedia , lookup
Proofs of Fermat's little theorem wikipedia , lookup
Non-standard analysis wikipedia , lookup
Computability theory wikipedia , lookup
Elementary mathematics wikipedia , lookup
List of first-order theories wikipedia , lookup
Birkhoff's representation theorem wikipedia , lookup
Material Taken From:
Mathematics
for the international student
Mathematical Studies SL
Mal Coad, Glen Whiffen, John Owen, Robert Haese,
Sandra Haese and Mark Bruce
Haese and Haese Publications, 2004
Topic 3 – Logic, Sets and
Probability
3.5 – Set Theory and Venn Diagrams
Basic Set Theory
• A set is a collection of numbers or objects.
- If A = {1, 2, 3, 4, 5} then A is a set that
contains those numbers.
• An element is a member of a set.
- 1, 2, 3, 4 and 5 are all elements of A.
- means ‘is an element of’ hence 4 A.
- means ‘is not an element of’ hence 7 A.
- means ‘the empty set’ or a set that
contains no elements.
Basic Set Theory
• If P and Q are sets then:
– P ⊆ Q means ‘P is a subset of Q’.
– Therefore every element in P is also an element
in Q.
For Example:
{1, 2, 3} ⊆ {1, 2, 3, 4, 5}
or
{a, c, e} ⊆ {a, b, c, d, e}
Basic Set Theory
• P Q is the union of sets P and Q meaning all
elements which are in P or Q.
• P ∩ Q is the intersection of P and Q meaning
all elements that are in both P and Q.
A = {2, 3, 4, 5}
AB=
A∩B=
and
B = {2, 4, 6}
Basic Set Theory
M = {2, 3, 5, 7, 8, 9} and N = {3, 4, 6, 9, 10}
• True or False?
I. 4 M
II. 6 M
•
List:
I. M ∩ N
II. M N
•
Is:
I. M ⊂ N ?
II. {9, 6, 3} ⊂ N?
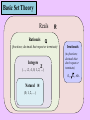
Basic Set Theory
Reals
Rationals
R
Q
(fractions; decimals that repeat or terminate)
Integers
Z
(…, -2, -1, 0, 1, 2, …)
Irrationals
(no fractions;
decimals that
don’t repeat or
terminate)
, 2, etc.
Natural N
(0, 1, 2, …)
Basic Set Theory
• N = {0, 1, 2, 3, 4, …} is the set of all natural numbers.
• Z = {0, + 1, + 2, + 3, …} is the set of all integers.
• Z+ = {1, 2, 3, 4, …} is the set of all positive integers.
• Z- = {-1, -2, -3, -4, …} is the set of all negative integers.
• Q = { p / q where p and q are integers and q ≠ 0} is the set
of all rational numbers (fractions).
• R = {real numbers} is the set of all real numbers. All
numbers that can be placed on a number line.
Basic Set Theory
Set Builder Notation describes the properties of the elements
of a set, using mathematical notation.
• The ’∣’ symbol means “such that.”
Example:
• D = { x ∣ 0 ≤ x ≤ 5 } – This is read “D is the set of all x such
that x is greater than or equal to 0 or less than or equal to 5.”
• It is important to note that this example lacks precision as it
does not specify what sort of numbers the set elements
should be (integers, rationals, etc.)?
Basic Set Theory
The number of elements in set A is denotes as n(A)
Example:
• G = { x ∣ x is a square number less than 50 }
• Assuming x is an integer then set G has 7 elements.
Thus, n(G) = 7
When a set has no elements, such as F = { p ∣ p is a prime number
and a multiple of 10} then n(F) = 0. This is called an empty set.
A set such as B = { 4, 5, 6, 7} contains a finite number of elements,
n(B) = 4, and is termed a finite set.
However, n(Z+) = ∞, so Z+ is termed an infinite set.
Basic Set Theory - Summary
Sets
⊆
N
Z
Q
R
Basic Set Theory - Summary
Sets
- is an element of
- is not an element of
⊆ - is a subset of
- union (everything)
- intersection (only what they share)
N – natural numbers
Z - integers
Q – rational numbers
R – real numbers
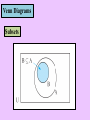
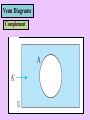
Venn Diagrams
The universal set (denoted U) must be
stated to make a set well defined.
U
The universal set U is shown
in diagrammatic as a rectangle.
A
This type of set is called a Venn Diagram.
Any set under consideration is shown as a
circle inside the universal set U.
Venn Diagrams
Example
U
A
Tuesday
Thursday
A universal set that
contains all the days of the
week that start with T or S.
Saturday
Sunday
Set A is defined
as all the days
that start with T.
Venn Diagrams
Subsets
If every element in a given set, M, is also an element of
another set, N, then M is a subset of N, denoted M ⊆ N
A proper subset of a given set is one that is not identical
to the original set.
If M is a proper subset of N (denoted M⊂ N) then:
1. Every element of M also lies in N and
2. There are some elements in N that do not lie in M
Venn Diagrams
U
N
M
•
•
•
•
If M is a proper subset of N then we write M ⊂ N
If M could be equal to N then we write M ⊆ N
Clearly, M and N are both subsets of the universal set U
In this Venn Diagram M ⊂ N ⊂ U
Venn Diagrams
Subsets
Venn Diagrams
Practice
Let U = {months of the year that end (in English) with ‘…ber’}
Let A = {months of the year that begin with a consonant}
Let B = {months of the year that have exactly 30 days}
Draw a Venn diagram to show:
a. Sets U and A
b. Sets U and B
c. Sets U, A and B
Venn Diagrams
Practice
U
A
October
September
November
December
Venn Diagrams
Practice
U
B
October
September
November
December
Venn Diagrams
Practice
U
A
September
B
November
December
October
Venn Diagrams
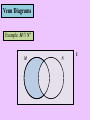
Intersection
The intersection of set A and B (denoted A ⋂ B)
is the set of all elements that are in both A and B.
A ⋂ B is the shaded
Venn Diagrams
Practice
Given the sets:
A = {1, 2, 3, 4, 5}
B = {x ∣0 < x ≤ 5, x ∈ Z}
C = {p ∣ p is a prime number and a multiple of 10}
D = {4, 5, 6, 7}
E = {x ∣ x is a square number less than 50}
Write down the sets:
a.
b.
c.
d.
A⋂D
A⋂B
D⋂E
C⋂D
Venn Diagrams
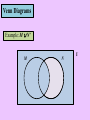
Union
The union of set A and B (denoted A ∪ B) is the set
of all elements that are in either A or B or both.
A ∪ B is the shaded region
Venn Diagrams
Practice
Given the sets:
A = {1, 2, 3, 4, 5}
B = {1, 2, 3, 4, 5}
C={∅}
D = {4, 5, 6, 7}
E = {1, 4, 9, 16, 25, 36, 49}
Write down the sets:
a. A ∪ D
b. A ∪ B
c. C ∪ D
Venn Diagrams
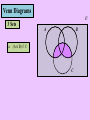
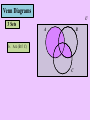
Complement
The complement of set M (denotes M’) is the set of all
the elements in the universal set that do not lie in M
M
N
M’ is the shaded region
U
Venn Diagrams
Example: M ∩ N’
M
N
U
Venn Diagrams
Example: M ∪ N’
M
N
U
Venn Diagrams
Complement
Venn Diagrams
Practice
U = {4, 5, 6, 7, 8, 9, 10}, F = {4, 5, 6, 7}, G = {6, 7, 8, 9}
a. Draw a Venn diagram for F , G and U
b. Write these sets: i) F’
ii) F ∩ G’
iii) (F ∩ G)’
Venn Diagrams
U
Practice
In this Venn diagram each
dot represents an element.
Write down:
a. n(G)
b. n(F)
c. n(G ∩ F)
d. n(H’)
e. n(F ∩ H)
f. n(G ∩ H)
Are these statements true or false?
g. n(F ∪H) = n(F) + n(H)
h. n(G ∪ H) = n(G) + n(H)
F
H
G
Venn Diagrams
U
3 Sets
B
A
Shade the region on the
Venn diagram that shows
the sets:
a. (A ∪ B) ∩ C
b. A ∪ (B ∩ C)
C
Venn Diagrams
U
3 Sets
B
A
a. (A ∪ B) ∩ C
C
Venn Diagrams
U
3 Sets
B
A
b. A ∪ (B ∩ C)
C
Venn Diagrams
Problem Solving
A teacher asks her class how many of them study
chemistry. She finds there are 15. She then asks
how many study biology and finds there are 13.
She also finds out that 5 students do not take any
science. There are 26 total students in the class.
15 + 13 + 5 = 33. Has she miscounted?
Venn Diagrams
Problem Solving
U
Represent this in a Venn
diagram with:
Chemistry = Set C = n(C) = 15
Biology = Set B = n(B) = 3
Total Class = Set U = n(U) = 26
No Science = n(B’ ∩ C’) = 5
B
C
13 6– x
x
7
158– x
5
Thus: (13 – x) + x + (15 – x) + 5 = 26
33 – x = 26
x=7
Venn Diagrams
Practice
In a class of 29 students, 19 study German, 14
study Hindi and 5 study both languages. Work out
the number of students that study neither language.
Venn Diagrams
n(G’∩H’) = 29 – (14+5+9) = 1
Practice
n(U) = 29, n(G) = 19, n(H) = 14 and n(G∩H) = 5
U
G
H
19 - 5
14
14 - 5
5
9
Venn Diagrams
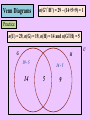
Practice
145 people answered a survey to find out which flavor of
fruit juice, orange, apple or grape the preferred. The replies
showed:
• 15 liked none of the three
• 55 liked grape
• 80 liked apple
• 75 liked orange
• 35 liked orange and apple
• 20 liked orange and grape
• 30 liked apple and grape
Find the number of people who liked all three types of juice
Basic Set Theory - Review
Notation
• set: A = {1, 3, 5}
• subset: P Q
– ‘P is a subset of Q’
{2, 3, 5} {1, 2, 3, 4, 5, 6}
Basic Set Theory - Review
Notation
•
‘is an element of’
– 3 {2, 3, 5}
•
‘is not an element of’
– 7 {2, 3, 5}
• n(A) number of elements in set A.
Basic Set Theory - Review
Notation
• Infinite Sets – sets with an infinite number of members.
o P = {0, 1, 2, 3, …}
o n(P) = ∞
• Finite Sets – sets that contain a finite number of members.
o A = {1, 2, 3}
o n(A) = 3
• Note: n( ) = 0
o = empty set
Basic Set Theory - Review
Set Builder Notation
A x x Z , 2 x 4
“the set of all x such that x is an integer
between -2 and 4, inclusive.”
Basic Set Theory - Review
Complementary Sets
If the universal set is:
U = {1, 2, 3, 4, 5, 6, 7, 8} and
A = {1, 3, 5, 7, 8} then
the complement of A, denoted A’ is
A’ = {2, 4, 6}
Basic Set Theory - Review
Notation
A A' 0
A A' U
n(A’) = n(U) – n(A)
Practice
Practice
Venn Diagrams - Review
Diagrams used to represents sets of objects, numbers or things.
U = {2,3,5,7,8}
A = {2,7,8}
A’ = {3,5
Venn Diagrams - Review
Disjoint Sets
Practice
Practice
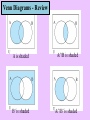
Venn Diagrams - Review
A is shaded
A∩B is shaded
B’ is shaded
A∩B’ is shaded
Practice