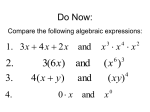Download Chapter 4b Factors

Chapter 4
Notes 4-2
Exponents
Parts of an Exponent
the base tells WHAT number
the exponent tells HOW MANY times
Example
3² means 3 x 3 = 9
−2 • a • a • a • b = −2a³b
be careful of negatives (−2 )² = (−2 )(−2 ) = 4
but
− 2 ² = − ( 2 • 2 ) = −4
________________________________________________________________________________
Notes 4-7 Multiplying Exponents
To multiply exponents with the same base,
write the base and add the exponents.
To multiply exponents with different bases,
multiply the base and simplify the exponents.
Taking a Power
TO A POWER!
This means (a²) 4 times (a²)(a²)(a²)(a²) means
multiply the exponents 2 x 4 = 8
a• a• a• a• a• a• a• a = a
_______________________________________________________________________________
Notes 4-8 Dividing Exponents
To divide exponents with the same base,
write the base and subtract the exponents.
You can also end up with only a denominator.
This can also be written with a negative exponent
(xy)
or on the bottom of a fraction.
Anything to the (0) exponent = 1
2³
2²
2¹
2°
=8
=4
=2
=1
2
=½
2
=¼
Follow the pattern. Each answer is cut in half.
Notes 5-9 Powers of products and Quotients
To Raise a PRODUCT to a power - raise each factor to the power.
(5 · 3)³ = 5³ · 3³ = 125 · 27 = 3375
To Raise a QUOTIENT to a power - raise both parts to the power.
_______________________________________________________________________________
Notes 4-9 Scientific Notation always has this form
One digit, a decimal, the rest of the number, X 10 to an exponent
To make the exponent,
count the spaces the decimal must move
to get to decimal to its right spot.
examples
6
2,000,000
=
2 X10
-5
0.00004
=
4 X10
BIG numbers have a POSITIVE exponent.
Little numbers have a NEGATIVE exponent.
STANDARD FORM is just a REGULAR NUMBER.
___________________________________________________________________________________________________________________
Notes 4-1
Divisibility and Factors
If a number ends in 2, 4, 6, 8, or 0, it is divisible by 2.
If a number ends in 5 or 0, it is divisible by 5.
Example
12 ÷ 2 = 6 (no remainder)
10 ÷ 5 = 2 (no remainder)
If you can add the digits of a number, and this new number is divisible by 3, 57 ÷ 3?
then you can divide the original number by 3.
5 + 7 = 12 (÷ 3 = 4)
57 ÷ 3 = 19
(ALSO) If the sum of the digits is divisible by 9, you can divide the number by 9.
If the sum of the digits is divisible by 3 and it is even, you can divide it by 6.
Vocabulary
factors
Description
numbers that divide evenly into another number.
Example
factors of 12 are 1, 2, 3, 4, 6, and 12
because 12 = 1x12, 2x6, 3x4
_______________________________________________________________________________________________________________________________________
Notes 4-3
Prime Factorization
Using the Sieve of Erotosthenes we find the PRIME numbers
Example 97 = 97x1 only
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 21, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, and 97
These numbers are divisible by ONLY itself and ONE.
Factor
means
Fracture
All other numbers are COMPOSITE numbers.
Use a factor tree to find the prime factorization.
= 2² • 3²
“Break it Down, Down,
Down”
Example 12 is composite (has many factors)
(“Break it Down, Down,
= 2² • 3²
Down”)
= 2² • 3²
It does not matter how we start, the end numbers (prime numbers) will be the same.
GCF, GCD GREATEST COMMON FACTOR, GREATEST COMMON DIVISOR (same thing)
The GCF is greatest (biggest) number that is divisible into both (or more) numbers.
Example
40 = 2 x 2 x 2 x 5
The factors that are the same are 2, 2, and 5 . . . 2 x 2 x 5 = 20.
60 = 2 x 2 x 3 x 5 The GCF of 40 and 60 is 20. 20 is the biggest number that is divisible into 40 and 60 evenly.
______________________________________________________________________________________________________________________________________
Notes 4-4
Simplifying Fractions
Divide the numerator and denominator by the same number.
All of these fractions equal ONE.
To SIMPLIFY, Factor, and get rid of common (same) factors from top and bottom.
Example
_____________________________________________________________________________