Download Drag and Drag Coefficients

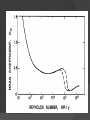
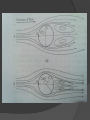
FLUID FLOW
OPERATIONS
Guided by :
Prof. Vaishali Umrigar
Prepared By :
MODI VATSAL D (140420105035 )
PANCHAL PRATIK (140420105037)
PANCHAL BHAVIK (140420105036)
SCET CHEMICAL FFO
FLOW PAST
IMMERSED
OBJECTS
CONTENTS….
Drag and Drag coefficients
 Drag Coefficients

 Drag coefficients equations
 Drag equation
Drag Coefficients of typical shapes
 Form drag and streamlining

 Stagnation point
 Stagnation pressure
The force in the direction of flow exerted by the fluid on the
solid is called Drag.
 By Newton’s third law of Motion, an equal and opposite force
is exerted by the object on the fluid.
 When the wall of the object is parallel with the direction of
flow, the only drag force is the wall shear.
 Another contribution comes from the fluid pressure which
acts in the direction normal to the wall.
 Here drag comes from the pressure component in the direction
of flow.
 The total drag on an element of area is the sum of the two
components.
 An extreme example is the Drag of a flat plate perpendicular
to the flow.




Fig shows the pressure and shear force acting on an
element of area dA inclined at an angle of (90-α) to the
direction of flow. The drag from wall shear is ‫ ح‬sin α
dA, and that from pressure is p cos α dA.
The total drag on the objects is the sum of the integrals
of these quantities, each evaluated over the entire
surface of the body in contact with the fluid.
The total integrated Drag from wall shear is called Wall
Drag and the total integrated drag from pressure is
called Form Drag.
In potential flow ‫ح‬w = 0, and there is no wall
drag. Also, the pressure drag in the direction of
flow is balanced by an equal force in the
opposite direction, and the integral of the form
drag is zero. There is no net drag in potential
flow.
The phenomena causing both wall and form
drag in actual fluids are complicated, and in
general the drag cannot be predicted. For
spheres and other regular shapes at low fluid
velocities, the flow patterns and drag forces can
be estimated from published correlations or by
numerical calculations using the general
momentum balance equations.
DRAG
COEFFICIENTS





In fluid dynamics, the drag coefficient is a dimensionless
quantity that is used to quantify the drag or resistance of an
object in a fluid environment, such as air or water.
It is used in the drag equation, where a lower drag coefficient
indicates the object will have less aerodynamic or
hydrodynamic drag. The drag coefficient is always associated
with a particular surface area.
The drag coefficient of any object comprises the effects of
the two basic contributors to fluid dynamic drag: Skin
friction and Form drag.
The drag coefficient of a lifting airfoil or hydrofoil also
includes the effects of lift-induced drag.
The drag coefficient of a complete structure such as an
aircraft also includes the effects of interference drag.
Drag Coefficients Equation
Where,
 F is the drag force, which is by definition the force
component in the direction of the flow velocity,
 rho is the mass density of the fluid,
 V is the flow speed of the object relative to the
fluid,
 r is the radius sphere.
Drag Equation
Where,
 F is the drag force,
 rho is the mass density of the fluid,
 V is the flow speed of the object relative to the
fluid,
 A is the reference area.
 Cd is the Drag coefficient.

For particles having shapes other than spherical, it is
necessary to specify the size & geometric form of the
object and its orientation with respect to the direction of
the flow of the fluid.
 One major dimension is chosen a the characteristic length,
and the other important dimension are given as ratios to the
chosen one.
 For dimensional analysis, the drag coeffient of a smooth
solid in an incompressible fluid depends upon a Reynolds
number and the necessary shape ratio.
 For a given shape,
 The Reynolds number for a particle in a fluid is defined
as,


Drag coefficient for compressible fluids increase
with an increase in the Mach number when the
letter becomes greater then 0.6.
Coefficient s in supersonic flow are generally
greater than in subsonic flow.
Drag coefficients of typical
shapes
In figure curves of CD versus Rep are shown for
spheres, long cylinders, & disks.
 The axis of the cylinder & the face of disks are
perpendicular to the direction of the flow, & this
curves apply only when this orientation is
maintained.
 The variations in slop of the curves of CD versus Rep
at different Reynolds numbers are the result of
interplay of various factors that control drag & wall
drag.

Stokes’ law is valid only when Rep is considerably
less than unity.
 The law is especially valuable for calculating the
resistance of small particles, such as dust fogs,
moving through gases or liquids of low viscosity or
for the motion of larger particles through highly
viscous liquid.
 As the Reynolds number increases beyond Rep = 1,
the flow pattern behind the sphere becomes different
from that in front of sphere.


At moderate Reynolds number of 200 to 300,
oscillations develop in the wake & vortices
disengage from the wake in a regular fashion,
forming in the downstream fluid a series of moving
vortices or a “vortex street”, as shown in figure.
Figure(a) shows the flow pattern for Rep = 105
where the boundary layer on the front part of sphere
is still laminar & the angle of separation is 85.
 When the front boundary layer becomes turbulent at
Rep = 3,00,000, the separation point moves toward
the rear of the sphere & the wake shrinks, as shown
in figure(b).

The Reynolds number at which the attached
boundary layer becomes turbulent is called
critical Reynolds for drag.
 The curves of CD versus Rep for an infinitely
long cylinder normal to the flow is much like
that for a sphere, but at low Reynolds numbers,
CD does not vary inversely with Rep because of
two-dimensional character of the flow around
the cylinder.

For short cylinders the drag coefficient falls
between the values for spheres & long cylinders
& varies inversely with Reynolds number at
very low Reynolds numbers.
 The drag coefficients for irregularly shaped
particles such as coal, sand are greater than
normal size.

Form drag and
Streamlining
Form drag can be minimized by forcing
seperation toward the rear of the object. This is
accomplished by streamlining. The usual method of
streamlining is to so proportion the rear of the object
that the increase in pressure in the boundary layer,
which is the basic cause of seperation, is sufficiently
gradual to delay seperation.
Streamlining usually calls for a pointed rear, like
that of an airfoil.
• A typical streamlined shape is shown in fig.
• A perfectly streamlined object would have no wake and little or no
form drag.
Stagnation Point
The streamlines in the fluid flowing
past the object in the fig. above shows that the
fluid stream in the plane of the section is split
by the object into two parts, one passing over
the top of the object and the other under the
bottom. Streamlines AB divides the two parts
and terminates at a definite point B at the nose
of the body. This point is called the Stagnation
Point.
The velocity at a Stagnation point is zero.
 Therefore, assuming that the flow is horizontal and friction along the
streamline is negligible,


(ps-p0 )/ρ = u0^2/2
 Where,
ps = pressure on body at stagnation point
p0 = pressure in undisturbed fluid
u0 = velocity of undisturbed fluid
ρ = density of fluid
The pressure increase ps-p0 for the streamline passing through a stagnation
point is larger than that for any other streamline, because at that point the
entire velocity head of the approaching stream is converted to pressure head.
Stagnation Pressure
Stagnation pressure (or pitot
pressure) is the static pressure at
a stagnation point in a fluid flow. At
a stagnation point the fluid velocity is zero
and all kinetic energy has been converted
into pressure energy (isentropically).