* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Drag and Drag Coefficients
Hemodynamics wikipedia , lookup
Airy wave theory wikipedia , lookup
Forces on sails wikipedia , lookup
Flight dynamics (fixed-wing aircraft) wikipedia , lookup
Fluid thread breakup wikipedia , lookup
Flow measurement wikipedia , lookup
Coandă effect wikipedia , lookup
Boundary layer wikipedia , lookup
Lift (force) wikipedia , lookup
Flow conditioning wikipedia , lookup
Compressible flow wikipedia , lookup
External ballistics wikipedia , lookup
Hydraulic machinery wikipedia , lookup
Navier–Stokes equations wikipedia , lookup
Derivation of the Navier–Stokes equations wikipedia , lookup
Computational fluid dynamics wikipedia , lookup
Wind-turbine aerodynamics wikipedia , lookup
Ballistic coefficient wikipedia , lookup
Bernoulli's principle wikipedia , lookup
Aerodynamics wikipedia , lookup
Reynolds number wikipedia , lookup
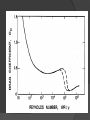
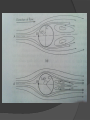
FLUID FLOW OPERATIONS Guided by : Prof. Vaishali Umrigar Prepared By : MODI VATSAL D (140420105035 ) PANCHAL PRATIK (140420105037) PANCHAL BHAVIK (140420105036) SCET CHEMICAL FFO FLOW PAST IMMERSED OBJECTS CONTENTS…. Drag and Drag coefficients Drag Coefficients Drag coefficients equations Drag equation Drag Coefficients of typical shapes Form drag and streamlining Stagnation point Stagnation pressure The force in the direction of flow exerted by the fluid on the solid is called Drag. By Newton’s third law of Motion, an equal and opposite force is exerted by the object on the fluid. When the wall of the object is parallel with the direction of flow, the only drag force is the wall shear. Another contribution comes from the fluid pressure which acts in the direction normal to the wall. Here drag comes from the pressure component in the direction of flow. The total drag on an element of area is the sum of the two components. An extreme example is the Drag of a flat plate perpendicular to the flow. Fig shows the pressure and shear force acting on an element of area dA inclined at an angle of (90-α) to the direction of flow. The drag from wall shear is حsin α dA, and that from pressure is p cos α dA. The total drag on the objects is the sum of the integrals of these quantities, each evaluated over the entire surface of the body in contact with the fluid. The total integrated Drag from wall shear is called Wall Drag and the total integrated drag from pressure is called Form Drag. In potential flow حw = 0, and there is no wall drag. Also, the pressure drag in the direction of flow is balanced by an equal force in the opposite direction, and the integral of the form drag is zero. There is no net drag in potential flow. The phenomena causing both wall and form drag in actual fluids are complicated, and in general the drag cannot be predicted. For spheres and other regular shapes at low fluid velocities, the flow patterns and drag forces can be estimated from published correlations or by numerical calculations using the general momentum balance equations. DRAG COEFFICIENTS In fluid dynamics, the drag coefficient is a dimensionless quantity that is used to quantify the drag or resistance of an object in a fluid environment, such as air or water. It is used in the drag equation, where a lower drag coefficient indicates the object will have less aerodynamic or hydrodynamic drag. The drag coefficient is always associated with a particular surface area. The drag coefficient of any object comprises the effects of the two basic contributors to fluid dynamic drag: Skin friction and Form drag. The drag coefficient of a lifting airfoil or hydrofoil also includes the effects of lift-induced drag. The drag coefficient of a complete structure such as an aircraft also includes the effects of interference drag. Drag Coefficients Equation Where, F is the drag force, which is by definition the force component in the direction of the flow velocity, rho is the mass density of the fluid, V is the flow speed of the object relative to the fluid, r is the radius sphere. Drag Equation Where, F is the drag force, rho is the mass density of the fluid, V is the flow speed of the object relative to the fluid, A is the reference area. Cd is the Drag coefficient. For particles having shapes other than spherical, it is necessary to specify the size & geometric form of the object and its orientation with respect to the direction of the flow of the fluid. One major dimension is chosen a the characteristic length, and the other important dimension are given as ratios to the chosen one. For dimensional analysis, the drag coeffient of a smooth solid in an incompressible fluid depends upon a Reynolds number and the necessary shape ratio. For a given shape, The Reynolds number for a particle in a fluid is defined as, Drag coefficient for compressible fluids increase with an increase in the Mach number when the letter becomes greater then 0.6. Coefficient s in supersonic flow are generally greater than in subsonic flow. Drag coefficients of typical shapes In figure curves of CD versus Rep are shown for spheres, long cylinders, & disks. The axis of the cylinder & the face of disks are perpendicular to the direction of the flow, & this curves apply only when this orientation is maintained. The variations in slop of the curves of CD versus Rep at different Reynolds numbers are the result of interplay of various factors that control drag & wall drag. Stokes’ law is valid only when Rep is considerably less than unity. The law is especially valuable for calculating the resistance of small particles, such as dust fogs, moving through gases or liquids of low viscosity or for the motion of larger particles through highly viscous liquid. As the Reynolds number increases beyond Rep = 1, the flow pattern behind the sphere becomes different from that in front of sphere. At moderate Reynolds number of 200 to 300, oscillations develop in the wake & vortices disengage from the wake in a regular fashion, forming in the downstream fluid a series of moving vortices or a “vortex street”, as shown in figure. Figure(a) shows the flow pattern for Rep = 105 where the boundary layer on the front part of sphere is still laminar & the angle of separation is 85. When the front boundary layer becomes turbulent at Rep = 3,00,000, the separation point moves toward the rear of the sphere & the wake shrinks, as shown in figure(b). The Reynolds number at which the attached boundary layer becomes turbulent is called critical Reynolds for drag. The curves of CD versus Rep for an infinitely long cylinder normal to the flow is much like that for a sphere, but at low Reynolds numbers, CD does not vary inversely with Rep because of two-dimensional character of the flow around the cylinder. For short cylinders the drag coefficient falls between the values for spheres & long cylinders & varies inversely with Reynolds number at very low Reynolds numbers. The drag coefficients for irregularly shaped particles such as coal, sand are greater than normal size. Form drag and Streamlining Form drag can be minimized by forcing seperation toward the rear of the object. This is accomplished by streamlining. The usual method of streamlining is to so proportion the rear of the object that the increase in pressure in the boundary layer, which is the basic cause of seperation, is sufficiently gradual to delay seperation. Streamlining usually calls for a pointed rear, like that of an airfoil. • A typical streamlined shape is shown in fig. • A perfectly streamlined object would have no wake and little or no form drag. Stagnation Point The streamlines in the fluid flowing past the object in the fig. above shows that the fluid stream in the plane of the section is split by the object into two parts, one passing over the top of the object and the other under the bottom. Streamlines AB divides the two parts and terminates at a definite point B at the nose of the body. This point is called the Stagnation Point. The velocity at a Stagnation point is zero. Therefore, assuming that the flow is horizontal and friction along the streamline is negligible, (ps-p0 )/ρ = u0^2/2 Where, ps = pressure on body at stagnation point p0 = pressure in undisturbed fluid u0 = velocity of undisturbed fluid ρ = density of fluid The pressure increase ps-p0 for the streamline passing through a stagnation point is larger than that for any other streamline, because at that point the entire velocity head of the approaching stream is converted to pressure head. Stagnation Pressure Stagnation pressure (or pitot pressure) is the static pressure at a stagnation point in a fluid flow. At a stagnation point the fluid velocity is zero and all kinetic energy has been converted into pressure energy (isentropically).