Download a + b

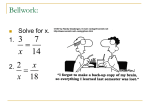
Lesson 8.1
Ratio: a ratio is a quotient of two
numbers.
a
b
a:b
a to b
Always given in lowest terms.
 Slope of a line is a ratio between
two points. (rise over run)
a÷b
Proportions: two or more ratios
set equal to each other.
a
c
=
b
d
a:b = c:d
a is the first term

b is the second term
c is the third term
d is the fourth term
Product and Ratio Theorems
In a product containing four terms:
First and fourth terms are the extremes.
Second and third terms are the means.
Theorem 59: In a proportion, the
product of the means is equal to
the product of the extremes.
(means-extremes product
theorem.)

a
c
=
b
d
 ad = bc
If they aren’t equal, then the ratios
aren’t in proportion.
Theorem 60: If the product of
 of non-zero numbers is
a pair
equal to the product of another
pair of non-zero numbers, then
either pair of numbers may be
made the extremes, and the
other pair the means, of a
proportion. (means-extremes
ratio theorem.)
This theorem is harder to state than to use!
Given: pq = rs
Then:

s
p
=
q
r
r
p
=
q
s
r
q
=
p
s
pq = rs
pq = rs
pq = rs

These proportions are all
 their cross
equivalent
 since
products are equivalent
equations.

Example:
a c
ab cd
If  , then

b d
b
d
2 x
x y
If  , then
?
3 y
y

Example:
a c
ac a
If  , then

b d
bd b
1 3
1 3
4 1
 , then
or 
2 6
26
8 2
Arithmetic Mean
Arithmetic means are just averages.
Given two numbers a and b,
find the arithmetic mean.
a+b
2
In a mean proportion,
the means are the same.
1 4
=
4 16

4 is the
geometric
 mean 
a
x
=
x
r
x is the
geometric
 mean
Definition: If the means in a proportion are equal,
either mean is called a geometric mean or mean
proportional between the extremes.
Find the arithmetic & geometry means
between 3 and 27.
Arithmetic mean:
3  27
2
= 15
Geometric mean:
3
x
=
x
27
x2 = 81
x=9
Solve:
Find the fourth term
(sometimes called the
fourth proportional) of a
proportion if the first
three terms are 2, 3,
and 4.
3
7
=
x
14
You might want
to reduce the
fraction first.

7x = 42
2
4
=
3
x
x=6
2x = 12
x=6


Find the mean proportional(s)
between 4 and 16.
4
x
=
x
16
x2 = 64
x=8
Notice that the principal or positive root is
taken although in algebra it could be either.
Since we will be dealing in measurement the
only one we are interested in is the positive.
Find the geometric mean between 12 and 6
Remember to simplify radicals. One of the rules for radicals is that
no factor of the radicand can be a perfect square.
72  36 2  6 2
If 3x = 4y, find the ratio of x to y.
Make x and 3 the extremes and y
and 4 the means.
3x = 4y
x
4
=
y
3



x a
Is =
y b
x  2y
a  2b ?
equal to
=
y
b
Cross multiply and simplify both sets.
ay = bx 
b(x-2y) = y(a-2b)

bx-2by = ay-2by
bx = ay
Yes, they are equal.