Download Acceleration

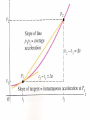
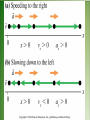
Acceleration
Physics
Montwood High School
R. Casao
Acceleration Defined
• Acceleration is defined as the change in
velocity per change in time.
• Velocity is speed and direction of motion.
• If speed changes, an acceleration is definitely
occurring.
• Acceleration involves a:
– change in speed.
– change in direction.
– change in speed and direction.
– Consider a car traveling at a constant 40 mph on a
long straight road.
– The car is NOT acceleration because neither its
speed or direction is changing. The car did
accelerate to get its speed up to 40 mph, but did not
accelerate after reaching 40 mph.
– Consider a car driving around a circular track at a
constant speed.
– The car IS accelerating. The speed is not changing,
but the direction of motion is changing. The
velocity is changing and the car is accelerating.
Types of Acceleration
• Increasing speed
– Example: Car speeds up at green light
• Decreasing speed
screeeeech
– Example: Car slows down at stop light
• Changing Direction
– Example: Car takes turn (can be at constant
speed)
Acceleration is a vector that points in the same
direction as the change in velocity.
v
v0
v
v0 + v = v
Acceleration is a vector that points in the same
direction as the change in velocity.
v0
v
v
v0 + v = v
• An object is accelerating when the velocity of
the object changes over time.
• Average acceleration is the the change in
velocity v divided by the change in time t.
a avg
Δv v f  v i


Δt
tf  ti
– Average acceleration is the slope of the secant line
between any two points on a velocity – time graph.
• The car moves from point A with velocity vi at time ti to
point B with velocity vf at time tf.
• The slope of the line connecting A to B represents the
average acceleration of the car between points A (vi) and
B (vf). Acceleration is the derivative of the velocity.
• The slope of the tangent line passing through point B
represents the instantaneous acceleration of the car at
point B.
• Acceleration is the slope of a velocity – time
graph (the derivative of the velocity).
• Acceleration has a magnitude and a direction
and is a vector quantity.
• Units: m/s2 (most common); ft/s2, or km/hr2.
• On a velocity – time graph:
– If a is positive:
• velocity is in the positive direction and the speed of the
object is increasing; acceleration is in the positive
direction.
• velocity is in the negative direction and the speed of the
object is decreasing; acceleration is in the positive
direction.
– If a is negative:
• velocity is in the positive direction and the speed of the
object is decreasing; the acceleration is in the negative
direction.
• velocity is in the negative direction and the speed of the
object is increasing; acceleration is in the negative direction.
– If a is zero, velocity is constant (not changing); the
object could be at rest. The slope of the velocity –
time graph is zero (rise = 0).
• When an object’s velocity and acceleration are in
the same direction, the object is speeding up.
• When an object’s velocity and acceleration are in
opposite directions, the object is slowing down.
(a) instantaneous acceleration
- equal to slope of the
tangent line through the
point of interest
(b) average acceleration
- equal to the slope of the
secant line between two
points on the graph
(c) zero acceleration
- no change in velocity
Visualizing Motion with Constant
Acceleration
Motion diagrams for three carts:
One-Dimensional Motion with Constant
Acceleration
• Constant or uniform acceleration means that the
velocity increases or decreases at the same rate
throughout the motion.
– The rate of change in the velocity is always the same.
• Variables to consider:
–
–
–
–
–
–
xo = initial displacement
xf = final displacement
vo = initial velocity
vf = final velocity
a = acceleration
t = time
• Velocity as a function of time:
vf  vi  a  t 
• Displacement as a function of time:
xf  xi

vi  vf   t

2

vi  vf   t
Δx 
2
2
Δx  v i  t   0.5  a  t


• Velocity as a function of displacement:
vf  vi  2  a  Δx 
2
2
• For motion in which a = 0 m/s2 (no change in
velocity):
– vi = vf
– Use the constant velocity equation:
Δx
v
t
• Often best to choose xo as 0 m at t = 0 s so that
the displacement x = xf (the final position).
• For an object at rest: vi = 0 m/s.
• For an object that stops: vf = 0 m/s.
• Examine the known variables before deciding
which equation to use to solve the problem.
• Don’t be too surprised if you have to use one
equation to find a variable and then use a
second equation to get the desired answer!
Distance in the nth second
• For problems involving the acceleration of an
object from an initial velocity without any
changes in acceleration, determine the distance
traveled during the nth second by using the
distance equation twice.
2
Δx  (vi  t)  (0.5  a  t )
• Example: determine the distance traveled during
the 2nd second. You are being asked to find the
distance the object travels from t = 1 s to t = 2 s.
• Find x for t = 2 s. Find x for t = 1 s. Subtract
to get x during the 2nd second.
• For multi-part problems in which the object has
changed its acceleration, you may have to
determine the initial velocity during the time
period in which you are asked to find the
distance traveled in the nth second.
• Ex. Object has constant acceleration for 5 s,
changes acceleration for the next 5 s. Determine
the distance traveled during the 8th second.
– You must find the distance traveled from t = 7 s to
t = 8 s.
– Determine the final velocity at the end of the 5 s; this
becomes the initial velocity for the next 5 s.
– Find x for t = 3 s (8s – 5 s, the second interval
begins at 5 s with the final velocity you just found
becoming the initial velocity vi for this interval of
time).
– Find x for t = 2 s (7 s – 5 s). Use the same initial
velocity vi that you used to find x for t = 3 s.
• Subtract to get x during the 8th second.
Graphing Acceleration:
Speed vs. Time Graphs
14
Speed (m/s)
12
10
8
6
4
2
0
0
1
2
3
4
5
6
Time (s)
1)Speed is increasing with time = accelerating
2)Line is straight = acceleration is constant
Graphing Acceleration:
Speed vs. Time Graphs
14
Speed (m/s)
12
10
8
Rise = 4 m/s
6
Run = 2 s
4
2
0
0
1
2
3
4
5
6
Time (s)
In Speed vs. Time graphs:
Acceleration = Rise/Run
Acceleration= 4 m/s ÷ 2 s = 2 m/s2
Graphing Acceleration:
Distance vs. Time Graphs
35
Distance (m)
30
25
20
15
10
5
0
0
1
2
3
4
5
Time (s)
1)On Distance vs. Time graphs a curved line means the
object is accelerating.
2)Curved line also means your speed is increasing.
Remember: slope = speed.
Graphical Look at Motion:
velocity – time curve
• The slope gives the
acceleration.
• The straight line
indicates a constant
acceleration.
Graphical Look at Motion:
acceleration – time curve
• The zero slope
indicates a constant
acceleration.
Graphical Motion with
Constant Acceleration
• A change in the
acceleration affects the
velocity and position.
• Note especially the
graphs when a = 0.
Acceleration – Time Graphs
The area under an acceleration-time graph is equal to the
change in velocity of the object.
• The area under the curve is the distance; the rectangle represents
vo·t and the triangle represents 0.5·a·t·t.
• The total distance represented under the curve is:

x  vo  t   0.5  a  t 2

• If you know the velocity of an object, can you tell me it’s
position?
– No. An object’s position is independent of the velocity.
– You would need to be told the position of the object.
• If you know the acceleration of an object, can you tell
me it’s velocity?
– No. An object’s velocity is independent of the acceleration.
– You would need to be told the velocity of the object.
• If you know only the velocity of an object, can you tell
me it’s acceleration?
– No. An object’s acceleration is the rate of change in velocity,
which is independent of the actual velocity at a given instant
(the instantaneous velocity).
– You would need to know the initial and final velocities of the
object to determine the acceleration.
Acceleration – Time Graphs Summarized
• the y-coordinate at any time gives the acceleration of the object
• horizontal graph segments indicate that the object has constant
acceleration
• a horizontal graph segment on the x-axis indicates that the object
has constant velocity (no acceleration)
• graph segments above the x-axis imply increasing velocities
• graph segments below the x-axis imply decreasing velocities
• no changes in direction may be inferred from these graphs
We typically only deal with constant acceleration situations, so
acceleration graphs generally consist of horizontal segments
only.
Question
14
Speed (m/s)
12
Run = 3 s
10
8
Rise = -6 m/s
6
4
2
0
0
1
2
3
4
5
6
Time (s)
Above is a graph showing the speed of a car over time.
1) How is the speed of the car changing (speeding up,
Slowing down, or staying the same)?
2) What is this car’s acceleration?
1) The car is slowing down
2) Acceleration = rise/run = -6m/s ÷3s = -2 m/s2
Question:
35
Distance (m)
30
25
20
15
10
5
0
0
1
2
3
4
5
Time (s)
The black and red lines represent
a objects that are
accelerating. Black is going a greater distance each second, so
it must be speeding up. Red is going less each second, so
1)Which
line
represents an object that is
must
be slowing
down
accelerating?
Remember: in distance vs. time graphs:
curved line = accelerating, flat line = constant speed
Example: The Aircraft Carrier
• Jet needs to be traveling 62 m/s for take-off
• Catapult can accelerate jet up to 31 m/s2
• How long does the carrier have to be?
Example: The Aircraft Carrier
What do we know?
v0 = 0 m/s
v = +62 m/s
a = +31 m/s2
What do we want to know?
x = ?
v  v0  at
1 2
x  v0t  at
2
Implied data!!
v  v  2ax
2
2
0
1
x  ( v0  v )t
2
Example: The Aircraft Carrier
v  v  2ax
2
2
0
2ax  v  v
2
2
0
v v
x
2a
2
2
(62 m / s)  (0 m / s)
x
 62 meters
2
2(31 m / s )
2
2
0
Approach to Problem Solving
1. Write down what you know in mathematical
terms. (e.g. v0=0 m/s) Is there any implied
data?
2. Write down what we are trying to figure out
(e.g. x=?).
3. Examine the relevant equations and choose
the one that will allow us to solve for the
quantity in 2) above.
4. Do the algebra!!
5. Plug in the numbers.
Example:
A spacecraft, traveling at +3250 m/s fires its reverse
thrusters to slow down. The thrusters slow the craft
down by 10 m/s every second.
What is its final velocity after travelling 215 km?
Example:
What do we know?
v0 = +3250 m/s
a = -10 m/s2
x = +215 km
= +215,000 m
What do we want to know?
v = ?
v  v  2ax
2
2
0
v  v0  at
1
x  ( v0  v )t
2
1 2
x  v0t  at
2
v  v  2ax
2
2
0
Example:
v  (3250 m / s)  2( 10 m / s )(215,000 m)
2
2
2
v  (3250 m / s)  2( 10 m / s )(215,000 m)
2
v  2500 m / s
2