Download SEM

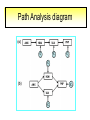
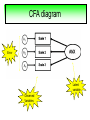
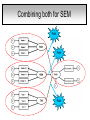
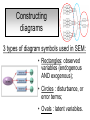
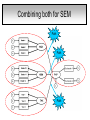
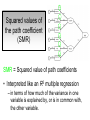
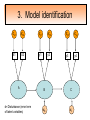
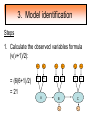
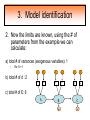
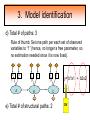
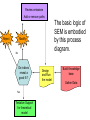
Structural Equation Modeling:
A simple-complex multivariate
technique
By:
Caroline Quesnel
Carole Scherling
Nancy Wallis
SEM
1.
2.
3.
4.
5.
6.
7.
8.
Categorization of SEM
Used in many fields
Path Analysis
Confirmatory Factor Analysis
Combining all for SEM analysis
Steps for SEM
Summary of SEM
Limitations and advantages
Categorization of SEM
• Since many different kinds of models fall
into each of the categories, structural
modeling as an enterprise is very difficult
to characterize.
• Major components include:
– Path analysis
– Confirmatory factor analysis
Categorization of SEM
• When SEM is useful:
– When you need to deal with latent
(unobserved) constructs.
– When you have a strong theoretical
background to your data (a priori hypothesis).
– When you are examining complex
relationships.
– When you have access to a large sample.
Not only in social sciences…
• Social Psychology
– Structural equation modeling the use of a risk assessment
instrument in child protective services
– A Structural Equation Model of Social Influences and Exposure
to Media Smoking on Adolescent Smoking
• Business/ Commerce
– Application of structural equation modeling to evaluate the
Intention of shippers to use Internet services in liner shipping.
– Human Capital and SME Internationalization: A Structural
Equation Modeling Study
• Health/Medicine
– Application of Structural Equation Modeling to Health Outcomes
Research
– Structural equation modeling of sleep apnea, inflammation, and
metabolic dysfunction in children
Not only in social sciences…
• Neurosciences
– Connectivity exploration with structural equation modeling: an
fMRI study of bimanual motor coordination
– Unified structural equation modeling approach for the analysis of
multisubject, multivariate functional MRI data
– A structural equation modeling analysis of attentional control: an
event-related fMRI study
• Cognition
– Validation of Cognitive Structures: A Structural Equation
Modeling Approach.
– Static and Dynamic Longitudinal Structural Analyses of Cognitive
Changes in Old Age
What is path analysis?
• Extension of multiple regression allowing us
to consider more than one DV at a time and
more importantly, allowing variables to be
both DVs AND IVs.
– In other words, it permits us to consider chains of
association, such that A can influence B, and B in
turn can affect C.
– Therefore, B is an DV because it’s affected by A,
but also an IV since it predicts C.
A
B
C
What is path analysis?
– New terminology:
• exogenous variable= Not influenced by any
other model variables
• endogenous variable = Influenced by other
model variables.
• Є= Error term of observed variables
– Limitation: can only handle variables
that are observed.
Path Analysis diagram
Є
Є
Є
Є
Є
Є
Extension of path analysis in SEM
• Instead of being limiting to drawing paths
among observed variables (as in path
analysis), in SEM we can draw paths
among latent variables.
– What are latent variables?
• Abstract, unobserved variables indirectly measured
through their effects on observable variables.
• IQ, self-esteem and depression are good examples.
Extension of path analysis in SEM
• EX: Evaluation of the accepted construct of
general intelligence (G) is done indirectly since
there is no direct way of observing it.
– How? If subjects perform well in
a range of assessed abilities
(observed variables), a higher G
score is attributed. However,
poor performance in the battery
leads to the assumption of a
poorer score for G.
But there’s more…
• SEM is also in part composed of a form
of factor analysis called Confirmatory
Factor Analysis or CFA.
• So, let’s now discuss CFA and how it
differs from the more commonly
encountered forms of factor analysis.
What is factor analysis (FA)?
• Originally, this technique was used to
EXAMINE/EXPLORE the data till
something “desired” was revealed.
• Premises:
– have many variables and want to examine if they can
be explained by a smaller number of factors.
– No a priori hypothesis (impossible to even indicate a
hunch to the program) as to which variables will
cluster together on which factor.
CFA presents a revised FA…
• The major difference is that an a priori hypothesis
is essential:
– which variables grouped together as manifestations of
an underlying construct and fits the model
• Like with path analysis, it can be helpful to draw
hypothesized relations in a diagram.
– Most commonly used computer programs, such as
LISREL (SSI, Lincolnwood, IL), AMOS (SPSS,
Chicago, IL), EQS (Multivariate Software, Encino, CA),
and Mplus (Muthén & Muthén, Los Angeles, CA),
accept these diagrams as input.
CFA ≠ model building
• With CFA, you stipulate where you think the variables
should load. Then, the program simply tells you whether
your model fits the data.
• If no fit, then there are few clues to guide you how to shuffle
the variables around to make the model better fit the data.
• Note: Even if the model does fit, it does not guarantee that a
new arrangement of variables would be an even better fit.
• Therefore, one must really use theory, knowledge, or
previous research to guide your model, rather than rely on
statistical criteria.
CFA diagram
Error
Latent
variable
Observed
Variables
Combining both for SEM
Path
Path
Path
Combining both for SEM
• Instead of being limited to drawing paths
among the measured variables, as we
were with path analysis, we can draw
paths among the latent variables.
• Each of the latent variables has ideally 3
or more associated measured variables,
so that each latent variable becomes a
small CFA in its own right.
Constructing
diagrams
3 types of diagram symbols used in SEM:
• Rectangles: observed
variables (endogenous
AND exogenous);
• Circles : disturbance, or
error terms;
• Ovals : latent variables.
Constructing
diagrams
Linking the symbols
• Direction of arrows between symbols are
important:
– for the analyses
– as a reflection of the underlying theory of
latent variables, CFA, and SEM in general.
Combining both for SEM
Path
Path
Path
Squared values of
the path coefficient
(SMR)
SMR = Squared value of path coefficients
• Interpreted like an R2 multiple regression
– in terms of how much of the variance in one
variable is explained by, or is in common with,
the other variable.
Error variances
Error variances = # over the arrows between the
error terms and the observed variables.
• NB: Σ (SMR + error variance per variable) = 1
– all the variance of a variable is divided between that
shared with the latent variable and error.
Path coefficients
Path coefficient is equivalent to the factor
loadings in FA.
• Therefore, this is a regression value.
– Standardized coefficients range: -1 to 1
– “> value” = stronger association
Steps to SEM
1.
2.
3.
4.
5.
6.
Assumptions
Model specification
Model identification
Model estimation
Model testing
Model modification (usually needed)
1. Assumptions
• Sample size: You must first compute the number
of possible parameters, knowing you need 10
participants / parameter.
• Normality: Collected data must be normally
distributed (but values of parameter estimates
are relatively robust).
• Independence: must be non-repeated measures
• Absence of outliers
• Absence of colinearity
2. Model specification
• Although no mathematics is involved, it is
probably the most difficult—and most
important—part.
• No use of computer aid.
• Draw out paths based on theory, literature,
and knowledge.
– NB: Correlations between observed variables
should not be significantly high (ex: an
individual correlation > 0.85 will cause the
program to crash)
3. Model identification
• Problem to solve: Possibility that the data will fit
more than one theoretical model equally well.
• If y+x = 10, therefore infinite number of possibilities
• Solution: Make sure to give the program more
information than you are asking from it. This in
order to not guess more parameters than you
should considering the number of observed
variables that you have.
• If y set at 2, y+x= 10, then x is solvable.
3. Model identification
Determine the # of parameters you have.
•
Formula: (v(v+1) / 2), where v= # of observed variables
•
Use of this formula, allows to see if trying to guess more
than the number of parameters the existing data allows.
•
Do not want to be JUST identified (cause lack of fit
indices) or UNDER identified, therefore looking to be
OVER-identified.
– Being OVER identified essentially means that there are more
available parameters than trying to estimate.
3. Model identification
Єx1
Єx2
Єy1
Єy2
Єy3
Єy4
X1
X2
y1
y2
y3
y4
A
d= Disturbance (error term
of latent variables)
B
C
dB
dc
3. Model identification
Steps
1. Calculate the observed variables formula
(v(v+1)/2):
= (6(6+1)/2)
= 21
Єx1
Єx2
Єy1
Єy2
Єy3
Єy4
X1
X2
y1
y2
y3
y4
A
B
C
dB
dc
3. Model identification
2. Now the limits are known, using the # of
parameters from the example we can
calculate:
a) total # of variances (exogenous variables): 1
–
Ex: A = 1
Єx1
Єx2
Єy1
Єy2
Єy3
Єy4
X1
X2
y1
y2
y3
y4
b) total # of d : 2
c) total # of Є: 6
A
B
C
dB
dc
3. Model identification
d) Total # of paths: 3
Rule of thumb: Set one path per each set of observed
variables to “1” (hence, no longer a free parameter, so
no estimation needed since it is now fixed).
Єx1
Єx2
Єy1
Єy2
Єy3
Єy4
X1
X2
y1
y2
y3
y4
1
1
1
A
B
C
dB
dc
e) Total # of structural paths: 2
y= b1x1 + b2x2
DV
3. Model identification
3. Now we must add up all the values:
1+2+6+3+2= 14
•
Please note that our task is much eased since
AMOS will tell you if you have the correct
number of parameters.
–
–
It will give you an error, or not run at all if it is underidentified.
NB: if your model is based on theory, identification
should not be an encountered problem.
Now, ready to analyze…
4. Model estimation
5. Model testing
Steps
A)
Run the model using the chosen program.
B)
Verify fit (Is this a good model?)
i) Chi-squared (recommended, but often does not work)
-Index for “badness” of fit : Non-significant value = good model.
-Very sensitive: keep results in mind but do not solely rely.
ii) Other indices calculations are:
-RMSEA: reasonable fit = 0.08; < 0.05 indicates a good fit.
- CFI and SRMR: range = 0 and 1 (interpreted as measures of
association or effect size); minimal acceptable value = 0.90 (except
with significant chi-squared, thereby requiring 0.95).
4. Model estimation
5. Model testing
Please note:
• Whenever you are presenting a preferred
model, it is also convention to demonstrate
that you have explored other models.
• It is up to the researcher to explain why the
preferred should not be rejected in favour of
statistically equivalent ones.
6. Model modification
• If indices indicate a poor fit, you
can do post-hoc modifications to
see if it is possible to achieve fit.
• Omission of variables,
• Dropping non-significant paths,
• Adding significant paths.
• Caveat: SEM is a knowledge based testing
statistical tool. Therefore, applying a post-hoc
modification can be a poor practice in theory.
6. Model modification
• NB: Must remember that it is unreasonable to
expect a structural model to fit perfectly.
– A structural model with linear relations is only an
approximation and the world is unlikely to be linear.
– So instead of asking “Does the model fit perfectly?”,
you must ask “Does it fit well enough to be a useful
approximation of reality and a reasonable explanation
of the trends in the data?”.
6. Model modification
• NB: Simply because a model
fits well, it does not prove that
the model is correct.
– Fit indicates the that you
are on the right track,
however you must
acknowledge the possibility
that it could also be wrong,
or that another could be
even better.
– Therefore, it is a fallacy to
affirm proof.
Review omissions
Add or remove paths
Reject
The basic logic of
SEM is embodied
by this process
diagram.
Modify
No
Do indices
reveal a
good fit ?
Yes
Tentative Support
for theoretical
model
Design
and Run
the model
Build Knowledge
base
Gather Data
Quick example of SEM (AMOS)
Screens of an SEM output
• http://www.creativewisdom.com/teaching/WBI/SEM.shtml
Limitations of SEM
• If there is not enough theoretical background, the model
WILL suffer.
• The model is only as good as the validated tests used in
the experiment to measure the observed variables.
Advantages of SEM
• Software is very user friendly.
• Allows models with latent variables.
• Studies complex multivariate relationships that
are closer to reality (vs. exploratory methods).
• Compensates for lack of perfect reliability in
measurement scales (therefore reveals true
relationship between variables).
• Due to necessary a priori hypothesis, yielded
model provides stronger evidence.
The End…
• Questions?
• Comments!