* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Choice modelling wikipedia , lookup
Interaction (statistics) wikipedia , lookup
Instrumental variables estimation wikipedia , lookup
Regression analysis wikipedia , lookup
Linear regression wikipedia , lookup
Expectation–maximization algorithm wikipedia , lookup
Time series wikipedia , lookup
PBF Zagreb, Croatia,
25.01. 2012
Structural Equation Modeling
- data analyzing -
Tatjana Atanasova – Pachemska,
„Goce Delcev” University - Shtip, Macedonia
1
Essentials
Purpose of this lecture is to provide a very brief presentation
of the things one needs to know about SEM before learning
how apply SEM.
2
Outline
I. Essential Points about SEM
II. Structural Equation Models: Form and Function
III. Research Examples
3
What is SEM?
• Structural equation modeling (SEM) is a series of statistical
methods that allow complex relationships between one or more
independent variables and one or more dependent variables.
• Though there are many ways to describe SEM, it is most
commonly thought of as a hybrid between some form of
analysis of variance (ANOVA)/regression and some form of
factor analysis. In general, it can be remarked that SEM allows
one to perform some type of multilevel regression/ANOVA on
factors. We should therefore be quite familiar with univariante
and multivariate regression/ANOVA as well as the basics of
factor analysis to implement SEM for our data.
4
• SEM goes beyond factor analysis to test expected
relationships between a set of variables and the factors upon
which they are expected to load. As such, it is considered
to be a confirmatory tool
• SEM also goes beyond multiple regression to demonstrate
how those independent variables contribute to explanation
of the dependent variable. It models the direction of
relationships within a multiple regression equation.
• The goal of SEM is to identify a model that makes
theoretical sense, is a good fit to the data . The model
developed should be theory-driven, or based on past
research.
5
I. SEM Essentials ( SEM language):
1. SEM is a form of graphical modeling, and therefore, a system
in which relationships can be represented in either graphical
or equational form.
equational
form
graphical
form
y1 = γ11x1 + ζ1
x1
11
1
y1
2. An equation is said to be structural if there exists sufficient
evidence from all available sources to support the
interpretation that x1 has a causal effect on y1.
6
3. Structural equation modeling can be defined as the use of
two or more structural equations to represent complex
hypotheses.
Complex
x1
y3
Hypothesis
ζ3
y1
Corresponding
Equations
e.g.
y2
ζ1
ζ2
y1 = γ11x1 + ζ1
y2 = β 21y1 + γ 21x1 + ζ 2
y3 = β 32y2 + γ31x1 + ζ 3
(gamma) used to represent effect of exogenous on endogenous.
(beta) used to represent effect of endogenous on endogenous 7
Some preliminary terminology will also be useful. The
following definitions regarding the types of variables that occur in
SEM allow for a more clear explanation of the procedure:
• Variables that are not influenced by another other variables in a
model are called exogenous (independent) variables.
• Variables that are influenced by other variables in a model are
called endogenous variables.
• A variable that is directly observed and measured is called an
indicator (manifest) variable. There is a special name for a
structural equation model which examines only manifest
variables, called path analysis.
• A variable that is not directly measured is a latent variable.
The “factors” in a factor analysis are latent variables.
8
Drawing our hypothesized model:
procedures and notation
The most important part of SEM analysis is
the causal model we are required to draw before
attempting an analysis. The following basic, general
rules are used when drawing a model:
• Rule 1. Latent variables/factors are represented
with circles and measured/manifest variables are
represented with squares.
9
Rule 2. Lines with an arrow in one direction show a hypothesized
direct relationship between the two variables. It should originate
at the causal variable and point to the variable that is caused.
Absence of a line indicates there is no causal relationship between
the variables.
Rule 3. Lines with an arrow in both directions should be curved
and this demonstrates a bi-directional relationship (i.e., a
covariance).
Rule 3a. Covariance arrows should only be allowed for
exogenous variables.
10
Rule 4. For every endogenous variable, a residual term
should be added in the model. Generally, a residual term is a
circle with the letter E written in it, which stands for error.
Rule 4a. For latent variables that are also endogenous, a
residual term is not called error in the lingo of SEM. It is called a
disturbance, and therefore the “error term” here would be a circle
with a D written in it, standing for disturbance.
11
12
SEM Process
A suggested approach to SEM analysis proceeds through the
following process:
• review the relevant theory and research literature to support
model specification
• specify a model (e.g., diagram, equations)
• determine model identification (e.g., if unique values can be
found for parameter estimation; the number of degrees of
freedom df, for model testing is positive)
13
• select measures for the variables represented in the model
• collect data
• conduct preliminary descriptive statistical analysis (e.g., scaling,
missing data, collinearity issues, outlier detection)
• estimate parameters in the model
• assess model fit
• respecify the model if meaningful
• interpret and present results.
14
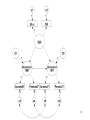
Examples
Figure 1. Regression Model (math achievement at age 10, reading
comprehension achievement at age 12, and mother’s educational
level predicting math achievement at age 12).
15
Figure 2. Revised model (math achievement at age 10, reading
comprehension at age 12 predict math achievement at age 12;
indirect effect of mother’s educational level and math achievement
at age 10).
16
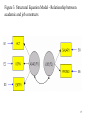
Figure 3. Structural Equation Model - Relationship between
academic and job constructs
17
A Grossly Oversimplified History of SEM
Contemporary
Wright
(1918)
path analysis
Joreskog
(1973)
Spearman
(1904)
Pearson
(1890s)
SEM
Lee
(2007)
Conventional
Statistics
Fisher
(1922)
Neyman & E. Pearson
(1934)
Bayes & LaPlace
(1773/1774)
MCMC
(1948-)
Raftery
(1993)
Bayesian
Analysis
Note that SEM is a framework and incorporates new statistical
18
techniques as they become available (if appropriate to its purpose)
The LISREL Synthesis
Karl Jöreskog
1934 - present
Key Synthesis paper- 1973
19
The Methodological Side of SEM
100
80
60
40
software
hyp testing
stat modeling
factor analysis
regression
20
0
20
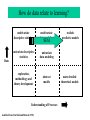
How do data relate to learning?
multivariate
descriptive statistics
multivariate
data modeling
univariate descriptive
statistics
univariate
data modeling
exploration,
methodology and
theory development
abstract
models
SEM
realistic
predictive models
Data
Understanding of Processes
modified from Starfield and Bleloch (1991)
more detailed
theoretical models
SEM is one of the few applications of statistical
inference where the results of estimation are frequently
“you have the wrong model!”. This feedback comes
from the unique feature that in SEM we compare
patterns in the data to those implied by the model. This
is an extremely important form of learning about
systems.
22
AMOS Graphics
AMOS (Analysis of MOments Structures) is a statistical
package specializing in structural equation modeling.
AMOS builds measurement, structural or full structural models.
It tests, modifies and retests models. AMOS also tests alternate
models, equivalence across groups or samples, as well as
hypotheses about means and intercepts. It handles missing data
using Maximum Likelihood (ML) estimation and provides
bootstrapping procedures.
Results obtained in AMOS are comparable to those obtained
through other SEM packages.
23
Five Steps to SEM
• Model specification;
• Model identifiability;
• Measure selection, data collection, cleaning and
preparation;
• Model analysis and evaluation;
• Model respecification
24
Model specification involves mathematically or diagrammatically
expressing hypothesized relationships among a set of variables.
The challenge at this step is to include all endogenous and exogenous
variables, (including moderators and mediators), that are expected to
contribute to central endogenous variables. Exclusion of important variables
may result in the misestimation of endogenous variables. The extent of
misestimation increases with the strength of the correlation between missing
and endogenous variables.
Whilst it is impossible to include all variables that contribute to the prediction
of endogenous variables, it is possible to identify the main ones through
careful examination of relevant theory and past research
A second challenge is to determine the direction of relationships between pairs
of variables in the SEM model. Actual direction is debatable, especially where
manifest variables are measured at the same point in time
25
Step 2: Model Identifiability
Specified models need to be checked for identifiability. A model is
theoretically identifiable if there is a unique solution possible for it
and each of its parameters. If a model is not identifiable, then it has
no unique solution and SEM software will fail to converge. Such
models need to be respecified to be identifiable.
The maximum number of parameters that can be specified in the
model is equivalent to the number of unique variances and
covariances that can be found in its underlying covariance matrix.
If, for example, there are four variables (say: A, B, C, and D), a
covariance matrix has four unique variances (one for each
variable) along with six unique covariances (AB, AC, AD, BC, BD
and CD), giving a total of ten unique parameters. (See figure).
26
A
B
C
D
A
Var(A)
Cov(AB)
Cov(AC)
Cov(AD)
B
Var(B)
Cov(BC)
Cov(BD)
C
Var(C )
Cov(CD)
D
Var(D)
A Covariance Matrix With Four Variables, A, B, C and D.
Note: For four variables, there are four unique variances and six unique
covariances, giving a maximum of ten
parameters estimable with SEM.
27
28
Step 3: Measure Selection, Data Collection, Cleaning and
Preparation
Step 3 has four substeps: measure selection, data collection, data
cleaning and data preparation
Step 3a - Measure Selection
Manifest variables are estimates of the underlying latent
constructs they purport to measure. It is therefore recommended
that each latent construct be measured by at least two manifest
variables.
Measures selected need to demonstrate good psychometric
properties. They need to be both “reliable” and “valid”
measure.
29
• Coefficients of 0.8 or above suggest good reliability,
whilst those in the range of 0.7 to 0.8 suggest adequacy.
Coefficients below 0.5 should be avoided or improved
before use in research.
• Validity is assessed by examining its content, criterionrelated, convergent or discriminant validities
• Content validity exists when experts agree that the
measure is tapping into the relevant domain.
• Criterion-related validity assesses whether a measure taps
into a particular domain, as assessed against some set
criteria
30
• Step 3b - Data Collection
• A sufficiently large sample needs to be drawn in order to
analyse the model specified at Step 1. The sample drawn
should be ten times the number of model parameters to
be estimated, with a minimum of 200 cases. If planning
to divide the sample in two for model development and
testing purposes, then each half sample needs to be
sufficiently large. Moreover, expected response rates
should be factored into consideration when drawing the
sample.
31
• Step 3c - Data “Cleaning”
• The acronym GIGO (Garbage In, Garbage Out) highlights
the importance of checking the veracity and integrity of data
entry. In statistical terms, doing so ensures that data is
“clean” before proceeding further.
• Checking each datapoint of a large dataset may be tedious.
However, it is possible to check (and correct) the first five
or ten cases and extrapolating their accuracy rate to the
remaining cases in the dataset. If accuracy is less than, say,
95%, the data could be reentered using a double entry
method.
32
II. Structural Equation Models: Form and Function
A. Anatomy of Observed Variable Models
33
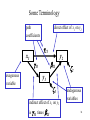
Some Terminology
path
coefficients
x1
exogenous
variable
direct effect of x1 on y2
21
11
21
y2
2
y1
1
indirect effect of x1 on y2
is 11 times
21
endogenous
variables
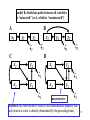
34
model B, which has paths between all variables
is “saturated” (vs A, which is “unsaturated”)
A
x1
y1
B
x1
y2
ζ1
y1
ζ2
C
y2
ζ1
ζ2
D
x1
y2
x1
y2
ζ2
x2
y1
ζ2
x2
ζ1
nonrecursive
y1
ζ1
recursive (the term recursive refers to the mathematical property that
each item in a series is directly determined by the preceding item).
35
First Rule of Path Coefficients: the path coefficients for
unanalyzed relationships (curved arrows) between
exogenous variables are simply the correlations
(standardized form) or covariances (unstandardized form).
x1
y1
.40
x2
x1
x2
y1
----------------------------x1
1.0
x2
0.40 1.0
y1
0.50 0.60 1.0
36
Second Rule of Path Coefficients: when variables are
connected by a single causal path, the path
coefficient is simply the standardized or unstandardized
regression coefficient (note that a standardized regression
coefficient = a simple correlation.)
x1
11 = .50
y1
21 = .60
y2
x1
y1
y2
------------------------------------------------x1
1.0
y1
0.50
1.0
y2
0.30
0.60
1.0
37
Third Rule of Path Coefficients: strength of a
compound path is the product of the coefficients along
the path.
x1
.50
y1
.60
y2
Thus, in this example the effect of x1 on y2 = 0.5 x 0.6 = 0.30
Since the strength of the indirect path from x1 to y2 equals the
correlation between x1 and y2, we say x1 and y2 are
conditionally independent.
38
What does it mean when two separated variables
are not conditionally independent?
x1
y1
y2
------------------------------------------------x1
1.0
y1
0.55
1.0
y2
0.50
0.60
1.0
x1
r = .55
y1
r = .60
y2
0.55 x 0.60 = 0.33, which is not equal to 0.50
39
The inequality implies that the true model is
x1
additional process
y2
y1
Fourth Rule of Path Coefficients: when variables are
connected by more than one causal pathway, the path
coefficients are "partial" regression coefficients.
Which pairs of variables are connected by two causal paths?
answer: x1 and y2 (obvious one), but also y1 and y2, which are connected by
40
the joint influence of x1 on both of them.
And for another case:
x1
y1
x2
A case of shared causal influence: the unanalyzed relation
between x1 and x2 represents the effects of an unspecified
joint causal process. Therefore, x1 and y1 connected by two
causal paths x2 and y1 likewise.
41
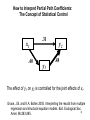
How to Interpret Partial Path Coefficients:
The Concept of Statistical Control
x1
.40
.31
y1
y2
.48
The effect of y1 on y2 is controlled for the joint effects of x1.
Grace, J.B. and K.A. Bollen 2005. Interpreting the results from multiple
regression and structural equation models. Bull. Ecological Soc.
42
Amer. 86:283-295.
Fifth Rule of Path Coefficients: paths from error
variables are correlations or covariances.
x1
.40
equation for path
from error variable
1 R
2
yi
.31
R2 = 0.44
y2
R2 = 0.16
.48
y1
.92
1
.84
.73
2
.56
alternative is to
show values for zetas,
which = 1-R2
43
Now, imagine y1 and y2
are joint responses
R2 = 0.25
.50
y2
2
.40
y1
1
x1
x1
y1
y2
------------------------------x1
1.0
y1
0.40 1.0
y2
0.50 0.60 1.0
R2 = 0.16
Sixth Rule of Path Coefficients: unanalyzed residual
correlations between endogenous variables are partial
correlations or covariances.
44
R2 = 0.25
.50
y2
2
.40
x1
.40
y1
1
R2 = 0.16
the partial correlation between y1 and y2 is typically
represented as a correlated error term
This implies that some other factor is influencing y1 and y2
45
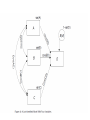
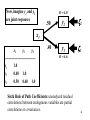
Seventh Rule of Path Coefficients: total effect one
variable has on another equals the sum of its direct and
indirect effects.
x1
.15
.64
.80
x2
-.11
y2
.27
ζ2
y1
Total Effects:
x1
x2
y1
------------------------------y1
0.64 -0.11 --y2
0.32 -0.03 0.27
ζ1
Eighth Rule of Path Coefficients:
sum of all pathways between two
variables (causal and noncausal)
equals the correlation/covariance.
note: correlation between
x1 and y1 = 0.55, which
equals 0.64 - 0.80*0.11
46
Suppression Effect - when presence of another
variable causes path coefficient to strongly differ from
bivariate correlation.
x1
.15
.64
.80
x2
-.11
y2
.27
ζ2
y1
x1
x2
y1
y2
----------------------------------------------x1
1.0
x2
0.80
1.0
y1
0.55
0.40
1.0
y2
0.30
0.23
0.35
1.0
ζ1
path coefficient for x2 to y1 very different from correlation,
(results from overwhelming influence from x1.)
47
II. Structural Equation Models: Form and Function
B. Anatomy of Latent Variable Models
48
Latent Variables
Latent variables are those whose presence we suspect or
theorize, but for which we have no direct measures.
fixed loading*
Intelligence
latent variable
1.0
IQ score
1.0
observed indicator
*note that we must specify some parameter, either error,
loading, or variance of latent variable.
ζ
error
variable
49
Latent Variables (cont.)
Purposes Served by Latent Variables:
(1) Specification of difference between observed data
and processes of interest.
(2) Allow us to estimate and correct for measurement error.
(3) Represent certain kinds of hypotheses.
50
Range of Examples
single-indicator
estimate
from map
multi-method
Elevation
soil C
loss on
ignition
repeated measures
singing range, t1
singing range, t2
Soil
Organic
repeatability
observer 1
Territory
Size
Caribou
Counts
observer 2
singing range, t3
51
The Concept of Measurement Error
the argument for universal use of latent variables
1. Observed variable models, path or other, assume all
independent variables are measured without error.
2. Reliability - the degree to which a measurement is
repeatable (i.e., a measure of precision).
illustration
25
20
y
15
x
10
0.60
y
5
R2 = 0.30
0
0
0.5
1
1.5
2
x
error in measuring x is ascribed to error in
predicting/explaining y
52
Example
Imagine that some of the observed variance in x is
due to error of measurement.
calibration data set based
on repeated measurement trials
plot
x-trial1 x-trial2 x-trial3
1
1.272 1.206 1.281
2
1.604 1.577 1.671
3
2.177 2.192 2.104
4
1.983 2.080 1.999
.
........
........
.......
n
2.460 2.266 2.418
average correlation between trials = 0.90
therefore, average R-square = 0.81
reliability = square root of R2
measurement error variance =
(1 - R2) times VARx
imagine in this case VARx = 3.14, so error variance = 0.19 x 3.14 = 0.60
.60
x
.90
LV1
.65
LV2
1.0
R2 = .42
y
53
II. Structural Equation Models: Form and Function
C. Estimation and Evaluation
54
1. The Multiequational Framework
(a) the observed variable model
We can model the interdependences among a set of predictors
and responses using an extension of the general linear model
that accommodates the dependences of response variables on
other response variables.
y = α + Βy + Γx + ζ
y = p x 1 vector of responses
α = p x 1 vector of intercepts
Β = p x p coefficient matrix of ys on ys
Γ = p x q coefficient matrix of ys on xs
Φ = cov (x) = q x q matrix of
covariances among xs
Ψ = cov (ζ) = q x q matrix of
covariances among errors
x = q x 1 vector of exogenous predictors
ζ = p x 1 vector of errors for the elements of y
55
(b) the latent variable model
η = α + Β η + Γξ + ζ
The LISREL
Equations
Jöreskög 1973
where:
η is a vector of latent responses,
ξ is a vector of latent predictors,
Β and Γ are matrices of coefficients,
ζ is a vector of errors for η, and
α is a vector of intercepts for η
(c) the measurement model
x = Λxξ + δ
y = Λyη + ε
where:
Λx is a vector of loadings that link observed x
variables to latent predictors,
Λy is a vector of loadings that link observed y
variables to latent responses, and
δ and ε are vectors are errors
56
Estimation Methods
(a) decomposition of correlations (original path analysis)
(b) least-squares procedures (historic or in special cases)
(c) maximum likelihood (standard method)
(d) Markov chain Monte Carlo (MCMC) methods
(including Bayesian applications)
57
Bayesian References:
Bayesian SEM:
Lee, SY (2007) Structural Equation Modeling: A Bayesian
Approach. Wiley & Sons.
Bayesian Networks:
Neopolitan, R.E. (2004). Learning Bayesian Networks. Upper
Saddle River, NJ, Prentice Hall Publs.
58
SEM is Based on the Analysis of Covariances!
Why? Analysis of correlations represents loss of information.
Illustration with regressions having same slope and intercept
A
100
80
y
60
y
40
r = 0.86
20
10
20
x
60
40
r = 0.50
20
0
0
0
B
100
80
30
0
10
20
30
x
Analysis of covariances allows for estimation of
both standardized and unstandardized parameters.
59
2. Estimation (cont.) – analysis of covariance structure
The most commonly used method of estimation over the past
3 decades has been through the analysis of covariance
structure (think – analysis of patterns of correlations among
variables).
compare
Observed Correlations*
S
=
{ }
1.0
.24 1.0
.01 .70 1.0
Model-Implied Correlations
Σ
=
σ11
σ12 σ22
σ13 σ23 σ33
{ }
* typically the unstandardized correlations, or covariances
60
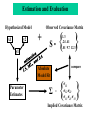
Estimation and Evaluation
Observed Covariance Matrix
Hypothesized Model
x1
y2
y1
+
S=
compare
Absolute
Model Fit
Parameter
Estimates
Σ
{ }
1.3
.24 .41
.01 9.7 12.3
=
σ11
σ12 σ22
σ13 σ23 σ33
{ }
Implied Covariance Matrix
Model Identification - Summary
1. For the model parameters to be estimated with unique
values, they must be identified. As in linear algebra, we
have a requirement that we need as many known pieces of
information as we do unknown parameters.
2. Several factors can prevent identification, including:
a. too many paths specified in model
b. certain kinds of model specifications can make
parameters unidentified
c. multicollinearity
d. combination of a complex model and a small sample
3. Good news is that most software (AMOS,…) checks for
identification (in something called the information matrix)
and lets you know which parameters are not identified. 62
Fitting Functions
The most commonly used fitting function in maximum likelihood
estimation of structural equation models is based on the log likelihood
ratio, which compares the likelihood for a given model to the
likelihood of a model with perfect fit.
FML
1
ˆ
ˆ
log Σ tr SΣ log S p q
Note that when sample matrix and implied matrix are equal, terms 1 and
3 = 0 and terms 2 and 4 = 0. Thus, perfect model fit yields a value of FML
of 0.
63
Fitting Functions (cont.)
Maximum likelihood estimators, such as FML, possess
several important properties: (1) asymptotically unbiased,
(2) scale invariant, and (3) best estimators.
Assumptions:
(1) and S matrices are positive definite (i.e., that they do not
have a singular determinant such as might arise from a
negative variance estimate, an implied correlation greater
than 1.0, or from one row of a matrix being a linear function
of another), and
(2) data follow a multinormal distribution.
64
Assessment of Fit between Sample Covariance and ModelImplied Covariance Matrix
The Χ2 Test
One of the most commonly used approaches to performing such tests (the
model Χ2 test) utilizes the fact that the maximum likelihood fitting function
FML follows a X2 (chi-square) distribution.
X2 = n-1(FML)
Here, n refers to the sample size, thus X2 is a direct function of sample size.
65
Illustration of the use of Χ2
correlation matrix
x
issue: should there be
a path from x to y2?
0.40
y1
y2
0.50
1.0
0.4 1.0
0.35 0.5
1.0
rxy2 expected to be 0.2
(0.40 x 0.50)
X2 = 1.82 with 1 df and 50 samples
P = 0.18
X2 = 3.64 with 1 df and 100 samples
P = 0.056
X2 = 7.27 with 1 df and 200 samples
P = 0.007
Essentially, our ability
to detect significant
differences from our
base model, depends as
usual on sample size.
66
Alternatives when data are extremely nonnormal
Robust Methods:
Satorra, A., & Bentler, P. M. (1988). Scaling corrections for chisquare statistics in covariance structure analysis. 1988
Proceedings of the Business and Economics Statistics
Section of the American Statistical Association, 308-313.
Bootstrap Methods:
Bollen, K. A., & Stine, R. A. (1993). Bootstrapping goodnessof-fit measures in structural equation models. In K. A.
Bollen and J. S. Long (Eds.) Testing structural equation
models. Newbury Park, CA: Sage Publications.
Alternative Distribution Specification: - Bayesian and other:
67
Diagnosing Causes of Lack of Fit (misspecification)
Modification Indices: Predicted effects of model
modification on model chi-square.
Residuals: Most fit indices represent average of residuals
between observed and predicted covariances. Therefore,
individual residuals should be inspected.
Correlation Matrix to be Analyzed
y1
y2
x
-------- -------- -------y1
1.00
y2
0.50
1.00
x
0.40
0.35
1.00
Fitted Correlation Matrix
y1
y2
x
-------- -------- -------y1
1.00
y2
0.50
1.00
x
0.40
0.20
1.00
residual = 0.15
68
Rewue of SEM
1. It is a “model-oriented” method, not a
null-hypothesis-oriented method.
2. Highly flexible modeling toolbox.
3. Can be applied in either confirmatory
(testing) or exploratory (model building) mode.
4. Variety of estimation approaches can be
used, including likelihood and Bayesian.
Where You can Learn More about SEM
Grace (2006) Structural Equation Modeling and Natural Systems.
Cambridge Univ. Press.
Shipley (2000) Cause and Correlation in Biology. Cambridge
Univ. Press.
Kline (2005) Principles and Practice of Structural Equation
Modeling. (2nd Edition) Guilford Press.
Bollen (1989) Structural Equations with Latent Variables. John
Wiley and Sons.
Lee (2007) Structural Equation Modeling: A Bayesian Approach.
John Wiley and Sons.
70
Thank you for your attention
71