Download 13.2 Explicit Sequences

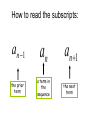
Sequences
What is a sequence?
A sequence of numbers is a list, an ordering that
may or may not follow some rule.
What are two types of Sequences?
• Arithmetic Sequence:
Is a sequence in which each term is equal to the previous term plus a
constant. This constant is called the common difference.
• Geometric Sequence:
Is a sequence in which each term is equal to the previous term
multiplied by a constant. This constant is called the common ratio.
When we are given a sequence and
asked to find a specific term…
1.Determine whether the sequence is arithmetic or
geometric.
2. Find the common difference (arithmetic) or the
common ratio (geometric)
3. Use the appropriate formula to find the
term asked for.
Arithmetic
An  a1   n  1 d
Geometric
An  a1r
n 1
We will be reviewing arithmetic
Find the common difference, find the indicated
term, write the equation in both function and
explicit form
Let’s look at a sequence.
12, 6, 0, -6, . . . Find a10
Write down every thing you need in the formula.
n =10 because we are looking for the 10th term
d = -6 because we are adding -6 to each term
a1 = 12 because it is the first term of the sequence
Now use the information in the formula…don’t
plug in “n” and you will have the explicit form
An  a1   n  1 d
An  12  (n  1)(6)
This is the explicit form
Distribute the -6 and simplify, change to f(n) and you will have
function form
f (n)  12  6n  6
f (n)  18  6n
This is function form
To find the 10th term use n = 10 and simplify
f (10)  18  6(10)
f (10)  42
So let’s list some steps
1. First find the common difference
2. Next list all of the unknowns
3. Find the explicit form by plugging in the
first term and the common difference
4. Find the function form by simplifying the
explicit form
5. To find the specific term replace n with
the term you are looking for.
You try…
Find the common difference, the indicated term,
write the explicit and function form of the
sequence.
1. 6,106, 206, 306,…n=15
2. -38,-45,-52,-59,…n=23
3. -16,14, 44, 74,…n=52
1406
-206
1574
What is a recursive sequence?
Definition: A recursive sequence is the
process in which each step of a pattern is
dependent on the step or steps before it.
Recursion Formulas:
A recursion formula defines the nth term of a sequence as a
function of the previous term. If the first term of a sequence
is known, then the recursion formula can be used to
determine the remaining terms.
Sequence and Terms
Let’s look at the following sequence
Do you know what the rule is for the sequence?
n²
1, 4, 9, 16, 25, 36, 49, …,
a1
a2
a3
a4
a5
a6
a7
The letter a with a subscript is used to represent
function values of a sequence.
The subscripts identify the location of a term.
How to read the subscripts:
an 1
the prior
term
an
a term in
the
sequence
an 1
the next
term
Example 1: Find the first four terms
of the sequence:
General Term
a1  5
an  3an1  2
Let’s be sure we understand what is given
a1  5
an

3an 1 + 2
is
The first
term is 5
Each term
after the
first
3 times the
previous
term
Plus 2
Continued…
EX 1: Find the first four terms of the sequence:
a1  5
an  3an1  2
Start with general term for n>1
n=1
a1  5
n=2
a2  3a21  2  3a1  2  3(5)  2  15  2  17
n=3
a3  3a31  2  3a2  2  3(17)  2  51  2  53
n=4
a4  3a41  2  3a3  2  3(53)  2  159  2  161
given
Answer = 5, 17, 53, 161
Your turn:
Ex 2: Find the next four terms of the sequence.
an  2an1
a1  3
Start with general term for n>1
n=1
a1  3
given
n=2
a2  2a21
 2a1
 2(3)  6
n=3
a3  2a31
 2a2
 2(6)  12
n=4
a4  2a41
 2a3
 2(12)  24
Answer = 3, 6, 12, 24
Write a recursive formula for the
arithmetic sequence below.
Step 1 : Make sure it is arithmetic
Step 2 : Plug into the arithmetic recursive formula.
Step 3 : Make sure you tell us what a1 is equal to.
Arithmetic
an  an 1  d
Ex. 3
7, 3, -1, -5, -9, …
The common difference = -4
an  an1  4
a1  7
The first
term = 7
Last Example 
Choose the recursive formula for the given
sequence.
Answer = C