Download spatial

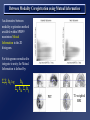
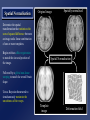
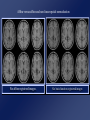
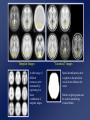
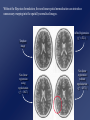
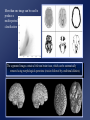
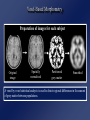
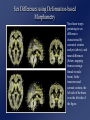
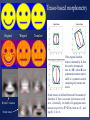
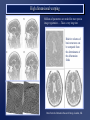
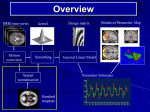
Computational Neuroanatomy
John Ashburner
[email protected]
•
•
•
•
•
•
Smoothing
Motion Correction
Between Modality Co-registration
Spatial Normalisation
Segmentation
Morphometry
Overview
Statistical Parametric Map
fMRI time-series
kernel
Design matrix
Motion
correction
smoothing
General Linear Model
Parameter Estimates
Spatial
normalisation
anatomical reference
Smoothing
• Why Smooth?
– Potentially increase signal to noise.
– Inter-subject averaging.
– Increase validity of SPM.
• In SPM, smoothing is a convolution with a Gaussian kernel.
• Kernel defined in terms of FWHM (full width at half maximum).
Gaussian convolution is separable
Gaussian smoothing kernel
Smoothing
Smoothing is done by convolving with a 3D Gaussian
- defined by its full width at half maximum (FWHM)
Each voxel after smoothing effectively becomes the
result of applying a weighted region of interest (ROI).
Before convolution
Convolved with a circle
Convolved with a Gaussian
Reasons for Motion Correction
The Steps in Motion
Correction
• Subjects will always move in the
scanner.
– movement may be related to the
tasks performed.
• When identifying areas in the brain that
appear activated due to the subject
performing a task, it may not be possible
to discount artefacts that have arisen due
to motion.
• The sensitivity of the analysis is
determined by the amount of residual
noise in the image series, so movement
that is unrelated to the task will add to
this noise and reduce the sensitivity.
• registration - i.e.
determining the 6
parameters that describe the
rigid body transformation
between each image and a
reference image.
• transformation - i.e. resampling each image
according to the determined
transformation parameters.
Registration
• Determine the rigid body transformation that minimises the sum of squared
difference between images.
• Rigid body transformation is defined by:
– 3 translations - in X, Y & Z directions.
– 3 rotations - about X, Y & Z axes.
• Operations can be represented as affine
transformation matrixes:
x1 = m1,1x0 + m1,2y0 + m1,3z0 + m1,4
y1 = m2,1x0 + m2,2y0 + m2,3z0 + m2,4
z1 = m3,1x0 + m3,2y0 + m3,3z0 + m3,4
Rigid body transformations parameterised by:
Translations
1

0
0

0
0
0
1
0
0
1
0
0
Xtrans
Pitch
1
 
Ytrans 0

Zt rans 0
 
1  0
Roll
0
0
cos()
sin()
sin()
cos()
0
0
0
 cos()
 
0  0

0 sin()
 
1  0
Yaw
0
sin()
1
0
0
cos()
0
0
0
 cos()
 
0 sin()

0  0
 
1  0
sin()
0
0
cos()
0
0
0
1
0
0
0
1


Residual Errors from PET
Transformation
•
Incorrect attenuation correction because transmission
scan no longer aligned with emission scans.
Residual Errors from fMRI
•
•
Gaps between slices can cause aliasing artefacts
Re-sampling can introduce errors
– especially tri-linear interpolation
•
d1
One if the simplest resampling methods is trilinear interpolation.
v1
– do not move according to the same rigid body rules as
the subject
v2
d3
d4
v4
Ghosts (and other artefacts) in the images
d2
•
– rapid movements not accounted for by rigid body model
v3
•
Other methods include nearest neighbour resampling, and various forms of sinc
interpolation using different numbers of
neighbouring voxels.
Slices are not acquired simultaneously
fMRI images are distorted
– rigid body model does not model these types of
distortion
•
Spin excitation history effects
– variations in residual magnetisation
Functions of the estimated motion parameters can be used as
confounds in subsequent analyses.
Between Modality Co-registration
• Not based on simply minimising mean
squared difference between images.
• A three step approach is used instead.
1) Simultaneous affine registrations between
each image and template images of same
modality.
2) Partitioning of images into grey and
white matter.
3) Final simultaneous registration of image
partitions.
Rigid registration between high resolution structural
images and echo planer functional images is a
problem. Results are only approximate because of
spatial distortions of EPI data.
First Step - Affine Registrations.
•
•
•
•
Requires template images of same modalities.
Both images are registered - using 12 parameter affine transformations - to
their corresponding templates by minimising the mean squared difference.
Only the rigid-body transformation parameters differ between the two
registrations.
This gives:
– rigid body mapping between the images.
– affine mappings between the images and the templates.
Second Step - Segmentation.
•
•
‘Mixture Model’ cluster analysis
to classify MR image (or images)
as GM, WM & CSF.
Additional information is
obtained from a priori
probability images, which are
overlaid using previously
determined affine
transformations.
Third Step Registration of
Partitions.
•Grey and white matter
partitions are registered
using a rigid body
transformation.
•Simultaneously minimise
sum of squared difference.
Between Modality Coregistration using Mutual Information
An alternative between
modality registration method
available within SPM99
maximises Mutual
Information in the 2D
histogram.
For histograms normalised to
integrate to unity, the Mutual
Information is defined by:
SiSj hij log
hij
Sk hik Sl hlj
PET
T1 weighted
MRI
Spatial normalisation
• Inter-subject averaging
– extrapolate findings to the population as a whole
– increase activation signal above that obtained from single subject
– increase number of possible degrees of freedom allowed in statistical model
• Enable reporting of activations as co-ordinates within a known standard space
– e.g. the space described by Talairach & Tournoux
• Warp the images such that functionally homologous regions from the different
subjects are as close together as possible
– Problems:
• no exact match between structure and function
• different brains are organised differently
• computational problems (local minima, not enough information in the images,
computationally expensive)
• Compromise by correcting for gross differences followed by smoothing of
normalised images
Spatial Normalisation
Original image
Spatially normalised
Determine the spatial
transformation that minimises the
sum of squared difference between
an image and a linear combination
of one or more templates.
Begins with an affine registration
to match the size and position of
the image.
Spatial Normalisation
Followed by a global non-linear
warping to match the overall brain
shape.
Uses a Bayesian framework to
simultaneously maximise the
smoothness of the warps.
Template
image
Deformation field
Affine versus affine and non-linear spatial normalisation
Six affine registered images.
Six basis function registered images
T2
T1
Transm
T1
305
EPI
PD
PET
PD
T2
Template Images
A wider range of
different
contrasts can be
normalised by
registering to a
linear
combination of
template images.
SS
“Canonical” images
Spatial normalisation can be
weighted so that non-brain
voxels do not influence the
result.
Similar weighting masks can
be used for normalising
lesioned brains.
Bayesian Formulation
• Bayes rule states: p(q|e)
 p(e|q) p(q)
– p(q|e) is the a posteriori probability of parameters q given errors e.
– p(e|q) is the likelihood of observing errors e given parameters q.
– p(q) is the a priori probability of parameters q.
• Maximum a posteriori (MAP) estimate maximises p(q|e).
• Maximising p(q|e) is equivalent to minimising the Gibbs potential of the
posterior distribution (H(q|e), where H(q|e)  -log p(q|e)).
• The posterior potential is the sum of the likelihood and prior potentials:
H(q|e) = H(e|q) + H(q) + c
– The likelihood potential (H(e|q)  -log p(e|q)) is based upon the sum of
squared difference between the images.
– The prior potential (H(q)  -log p(q)) penalises unlikely deformations.
Spatial Normalisation - affine
• The first part of spatial normalisation is a
12 parameter Affine Transformation
–
–
–
–
3 translations
3 rotations
3 zooms
3 shears
Empirically generated priors
1


0

0

0
0 0 Xtrans   1
0
0
1 0 Ytrans   0 cos() sin( )

0 1 Ztrans   0  sin( ) cos()
0 0
1
 
 0
0
0
 cos()

0   0

0    sin( )
 
1  0
0 
0 sin( ) 0 
1
0
0 cos()
0
0
 cos()

0    sin( )

0   0
 
1  0
sin( ) 0 0 
cos() 0 0 
0
1 0 
0
0 1

 Xzoom


0
 
 0

 0
0
0
Yzoom
0
0
0
0   1 XYshear XZshear 0 
1
Zzoom
0   0

0   0
0
1
0 
0
1  0
0
0
1
 
YZshear 0 
Find the parameters that minimise the sum of squared difference between the
image and template(s) - and also the square of the number of standard deviations
away from the expected parameter values.

Spatial Normalisation - Non-linear
• Deformations consist of a linear
combination of smooth basis images.
• These are the lowest frequency basis
images of a 3-D discrete cosine
transform (DCT).
• Can be generated rapidly from a
separable form.
•
Algorithm simultaneously minimises
– Sum of squared difference between
template and object image .
– Squared distance between the
parameters and their known expectation
(pTC0-1 p).
•
pTC0-1 p describes the membrane
energy of the deformations.
2
2 2

u
 ji 

membrane energy =   

x
i j 1 k 1 
ki 
Without the Bayesian formulation, the non-linear spatial normalisation can introduce
unnecessary warping into the spatially normalised images.
Affine Registration.
(2 = 472.1)
Template
image
Non-linear
registration
using
regularisation.
(2 = 302.7)
Non-linear
registration
without
regularisation.
(2 = 287.3)
Segmentation.
•
•
•
•
‘Mixture Model’ cluster analysis to classify
MR image (or images) as GM, WM & CSF.
Additional information is obtained from
prior probability images, which are overlaid.
Assumes that each MRI voxel is one of a
number of distinct tissue types (clusters).
Each cluster has a (multivariate) normal
distribution.
.
•
A smooth intensity
modulating function can
be modelled by a linear
combination of DCT
basis functions.
More than one image can be used to
produce a
multi-spectral
classification.
The segmented images contain a little non-brain tissue, which can be automatically
.
removed using morphological operations
(erosion followed by conditional dilation).
Morphometric Measures
• Voxel-by-voxel
– where are the differences between
the populations?
– produce an SPM of regional
differences
• Univariate - e.g., VoxelBased Morphometry
• Multivariate - e.g., TensorBased Morphometry
• Volume based
– is there a difference between the
populations?
• Multivariate - e.g.,
Deformation-Based
Morphometry
MANCOVA & CCA
Voxel-Based Morphometry
Preparation of images for each subject
Original
image
Spatially
normalised
Partitioned
grey matter
Smoothed
A voxel by voxel statistical analysis is used to detect regional differences in the amount
of grey matter between populations.
Morphometric approaches based on deformation fields
Deformation-based Morphometry
looks at absolute displacements.
Tensor-based Morphometry looks
at local shapes
Deformation-based morphometry
Deformation
fields
...
Remove positional and size information - leave shape
Parameter reduction using principal component analysis (SVD).
Multivariate analysis of covariance used
to identify differences between groups.
Canonical correlation analysis used to
characterise differences between groups.
Sex Differences using Deformation-based
Morphometry
Non-linear warps
pertaining to sex
differences
characterised by
canonical variates
analysis (above), and
mean differences
(below, mapping
from an average
female to male
brain). In the
transverse and
coronal sections, the
left side of the brain
is on the left side of
the figure.
Tensor-based morphometry
Original
Warped
Template
If the original Jacobian
matrix is donated by A, then
this can be decomposed
into: A = RU, where R is an
orthonormal rotation matrix,
and U is a symmetric matrix
containing only zooms and
shears.
Relative volumes
Strain tensor
Strain tensors are defined that model the amount of
distortion. If there is no strain, then tensors are all
zero. Generically, the family of Lagrangean strain
tensors are given by: (Um-I)/m when m~=0, and
log(U) if m==0.
High dimensional warping
Millions of parameters are needed for more precise
image registration….. Takes a very long time
Relative volumes of
brain structures can
be computed from
the determinants of
the deformation
fields
Data From the Dementia Research Group, London, UK.
References
Friston et al (1995): Spatial registration and
normalisation of images.
Human Brain Mapping 3(3):165-189
Ashburner & Friston (1997): Multimodal image
coregistration and partitioning - a unified
framework.
NeuroImage 6(3):209-217
Collignon et al (1995): Automated multi-modality
image registration based on information theory.
IPMI’95 pp 263-274
Ashburner et al (1997): Incorporating prior
knowledge into image registration.
NeuroImage 6(4):344-352
Ashburner et al (1999): Nonlinear spatial
normalisation using basis functions.
Human Brain Mapping 7(4):254-266
Ashburner & Friston (2000): Voxel-based
morphometry - the methods.
NeuroImage 11:805-821