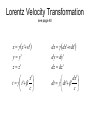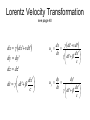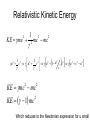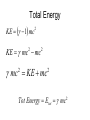Download File - USNA

Chapter 02
Special Relativity
Version 110906, 110907, 110908, 110913
General Bibliography
1) Various wikipedia, as specified
2) Thornton-Rex, Modern Physics for Scientists & Eng, as indicated
Outline
•
•
•
•
•
•
Galilean Transformations
Names & Reference Frames
The Ether River
Michelson-Morley Experiments
Einstein Postulates
Lorentz Transformations
– Position
– Velocity
•
•
•
•
Space-Time Diagrams
Relativistic Forces & Momentum
Relativistic Mass
Relativistic Energy
CLASSICAL / GALILEAN / NEWTONIAN
TRANSFORMATIONS
Galilean Transformations
K’ frame moving with speed v
K frame fixed
v
K & K’ coincided at t=0. Sketch shown at time t later.
How do the position, velocity, acceleration, & time between the 2 frames compare?
 x
 
 y
z
 
t
 
 vx 
 
 vy 
v 
 z
 ax 
 
 ay 
a 
 z


ma   F
 x' 
 
 y'
 z' 
 
 t' 
 
 v x' 
 '
 vy 
 v' 
 z
 a x' 
 '
 ay 
 a' 
 z


ma '   F
Galilean Transformations
K’ frame moving with speed v
K frame fixed
v
K & K’ coincided at t=0. Sketch shown at time t later.
How do the position, velocity, acceleration, & time between the 2 frames compare?
K  K’
K’  K
x = x’ + vt
x = x’ - vt
Newtonian Principle of Relativity
• If Newton’s laws are valid in one reference
frame, then they are also valid in another
reference frame moving at a uniform
velocity relative to the first system.
• This is referred to as the Newtonian
principle of relativity or Galilean
invariance.
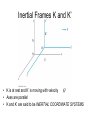
Inertial Frames K and K’
• K is at rest and K’ is moving with velocity
• Axes are parallel
• K and K’ are said to be INERTIAL COORDINATE SYSTEMS
The Galilean Transformation
For a point P


In system K: P = (x, y, z, t)
In system K’: P = (x’, y’, z’, t’)
P
x
K
K’
x’-axis
x-axis
Conditions of the Galilean
Transformation
• Parallel axes (for convenience)
• K’ has a constant relative velocity in the x-direction
with respect to K
x’ = x – v t
y’ = y
z’ = z
speed of frame
NOT speed of object
t’ = t
• Time (t) for all observers is a
Fundamental invariant,
i.e., the same for all inertial observers
Galilean Transformation
Inverse Relations
Step 1. Replace
with
.
Step 2. Replace “primed” quantities with
“unprimed” and “unprimed” with “primed.”
x = x’ + v t
y = y’
z = z’
t = t’
speed of frame
NOT speed of object
Position
General Galilean Transformations
x  x'vt
y  y'
t  t'
Velocity
t and t ' are the same
dx dx'

 v  u x  u x ' v
dt dt
dy dy '

 t y  t'y
dt dt
dt dt '

11
dt dt
inertial reference frame
t and t ' are the same
dx dx'

 v  v x  v' x v
dt dt
dy dy '

 v y  v' y
dt dt
dt dt '

11
dt dt
Acceleration
frame K
t and t ' are the same
dv x dv x '

 0  ax  ax '
dt
dt
dv y dv y '

 a y  a' y
dt
dt
frame K’


ma   F  ma'   F
Newton’s Eqn of Motion the same at
face-value in both reference frames
Classical Reference Frames
• Inertial Reference Frame
– Non-accelerating
– Newton’s Laws apply at face-value
• Non-Inertial Reference Frame
– Examples:
• Rocket during acceleration phase
• Rotating merry-go-round
• Rotating Earth
Youtube clips (part 1)
• Galilean/Classical Relativity
Part 1 – The Cassiopeia Project
http://www.youtube.com/watch?v=6rl3Z9yCTn8
The Cassiopeia Project is an effort to make high quality science videos available to everyone.
If you can visualize it, then understanding is not far behind.
http://www.cassiopeiaproject.com/
To read more about the Theory of Special Relativity, you can start here:
http://www.phys.unsw.edu.au/einsteinlight/
http://www.einstein-online.info/en/elementary/index.html
http://en.wikipedia.org/wiki/Special_relativity
THE ETHER RIVER
HISTORY OF ETHER
MICHELSON-MORLEY EXPTS
The Ether River
v
D
C
A
Maximum speed of the boat is ‘c’ meters/sec
The Ether River
Time t1 from A to C and back:
Time t2 from A to D and back:
t2 
2 2
c v
2
2

2 2
1

2
c
v
1
c2
So that the difference in trip times is:
t  t 2  t1 

2 
2

c  1 v2

2
c


1 


2
1  v 2 
c 
Timeline of luminiferous aether
(http://en.wikipedia.org/wiki/Timeline_of_luminiferous_aether)
•
•
•
•
4th cent BC – Light propagates in air – Aristole
1704 – Aetheral medium for light & heat – Newton
1818 – aether – Fresnel wave theory
1830 – problems emerge, explained by “aether drag”, Fresnel &
Stokes
• 1830 – ~1955 – mixed experimental conclusions
Cronholm144, http://en.wikipedia.org/wiki/File:AetherWind.svg
Timeline of luminiferous aether
(http://en.wikipedia.org/wiki/Timeline_of_luminiferous_aether)
Cronholm144, http://en.wikipedia.org/wiki/File:AetherWind.svg
• 1830 – ~1955 – mixed experimental conclusions
•
•
•
•
•
1887 – 1st Michelson-Morley expt doesn’t find aether
1889(1895) – Fitzgerald hypothesis (Lorentz)
1902-1904 – Refined Michelson-Morley measurements
1905 – Trouton-Rankine expt doesn’t support Fitz-Loentz hypothesis
1958- nearly all measurements do not find evidence for aether
Cronholm144, http://en.wikipedia.org/wiki/File:AetherWind.svg
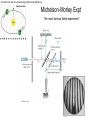
Michelson-Morley Expt
“the most famous failed experiment”
Michelson-Morley:
Ether River - Revisited
v
D
v
D
C
A
C
A
Measure two orientations because don’t know direction of aether river
Ether River - Revisited
Orientation 1
torient1  t 2  t1 

2 
2

c  1 v2

c2


1 


2
v

1
c 2 
Orientation 2
torient2  t 2  t1 

2  2

c  1 v2 2

c




1

2
1  v 2 
c 
Difference in Orientations
torient1  torient2 

2  1   2

c  1 v2 2

c



1   2 
1
v2
 
1   2  2
2
c
c
1  v 2 
c 
Michelson-Morley Measurements
Apollo 11
Apollo 15
v=30 km/s
c=3E8 m/s
~2002
accuracy
~1 mm
http://en.wikipedia.org/wiki/Lunar_Laser_Ranging_Experiment
l1+l2
to1-to2
(m)
(sec)
1887
2*1.5
1E-16
30 nm
~1903
2*30
2E-15
600 nm
Earth-Moon
3.8E8
1.3E-8
3.8 m
c[to1-to2]
Crises with Reference Frame
Xformations
• Can’t find the Ether
• Maxwell’s Equations not Galilean Invariant
Speed of Light fixed by EM constants
c
1

Fitzgerald-Lorentz Hypothesis
1889 (1895)
{only a partial explanation}
POSTULATE: the null results are due to changes in length in the direction of travel.
1
L  L
2 2
torient1  t 2  t1 
torient2  t 2  t1 
c v
2
2 2
c v
2
2

2

2
v
1

2 
2

c  1 v2

c2


2  2

c  1 v2 2

c

c2

1 


2
v

1
c 2 



1

2
1  v 2 
c 
torient1  torient2  0
EINSTEIN’s 1905 POSTULATES
• All laws for physics have the same
functional form in any inertial reference
frame
• Speed of Light (in vacuum) is same in any
inertial reference frame.
LORENTZ
POSITION-TIME
TRANSFORMATIONS
Lorentz Transformations
K’
K
v
x
K’ K
P
x’
x’-axis
x-axis
x '    x  vt 
y'  y
z'  z
x

t'   t   
c


1
1  2

v
c
Lorentz Transformations
K’
K
K K’
v
x
P
x’
x’-axis
x-axis
x    x'vt'
y  y'
z  z'
x' 

t    t '  
c


1
1  2
v

c
K: 3km, 5us
K’: 2.6km, -1.25us
Example
As observed from a large asteroid, an explosion occurs at
x=3000, y=500, z=-500 and t=5 us.
v
P
A spaceship approaches at a high speed v=0.6c .
The reference frames coincided at t=0, t’=0
At what position does the spaceship observe the explosion to occur?
K rear -5km, -10 us
front +5km, +10 us
Example
The reference frames coincide at x=0, x’=0 & t=0, t’=0
A spaceship has indicator lights which are flashed at the same time.
At t’=0 the lights flash. The locations of the lights are x’rear=4km & x’front=+4km.
K’
K
v
x’-axis
x-axis
The spaceship is observed from the spacestation.
The spaceship is observed to move at v=0.6c .
At what position does the spacestation observe the lights to flash?
Example
0m, 2.3 s
6.5E8, 3.2 s
The reference frames coincide at x=0, x’=0 & t=0, t’=0
As viewed from the Earth, a meteorite impacts the lunar surface at 3E8m and 2.5s .
The impact is observed from 2 passing spaceships,
one traveling to the right at 40% c
and the other to the left at  40% c.
Where do the 2 spaceships observe the impact to occur ?
Length Contraction
(Lorentz-Fitzgerald)
A meter stick, lying parallel to the x-axis, is moving with speed v
v
How long does the stick appear to be to a stationary observer
who makes the observation of the length at t=0?
xleft & tleft=0
xright & tright=0
Moving
objects
appear
shorter
Time Dihilation
(distinct from the L-F)
A clock, located at x’=0, makes ticks at t’1, t’2, …
v
What is the interval between ticks to a stationary observer,
who observes the clock to move at speed v?
x’1=0 & t’1
x’2=0 & t’2
Moving
clocks
run
slow
Distorted Pictures
stationary
moving to the right
Our brain records photographs (frames in a movie)
– light rays arriving at the same time.
“Jump to Light Speed”
Distorted Pictures
Lorentz Transformation - Derivation
Light propagates with speed c in all inertial reference frames
K’
K
ct
Spherical wavefronts in K:
Spherical wavefronts in K’:
ct’
Derivation – see pages 30-31
1) Let x’ = (x – vt) so that x =
(x’ + vt’)
2) By Einstein’s first postulate:
3) The wavefront along the x,x’- axis must satisfy:
x = ct and x’ = ct’
4) Thus ct’ =
(ct – vt) and ct = (ct’ + vt’)
5) Solving the first one above for t’ and substituting
into the second...
Youtube clips (part 2)
• Galilean/Classical Relativity
Part 2 – The Cassiopeia Project
http://www.youtube.com/watch?v=WgsKlSnUO0k
The Cassiopeia Project is an effort to make high quality science videos available to everyone.
If you can visualize it, then understanding is not far behind.
http://www.cassiopeiaproject.com/
To read more about the Theory of Special Relativity, you can start here:
http://www.phys.unsw.edu.au/einsteinlight/
http://www.einstein-online.info/en/elementary/index.html
http://en.wikipedia.org/wiki/Special_relativity
LORENTZ
VELOCITY
TRANSFORMATIONS
Lorentz Velocity Transformation
see page 40
x    x'vt'
dx   dx ' vdt'
y  y'
dy  dy '
z  z'
dz  dz '
x' 

t    t '  
c

dx ' 

dt    dt ' 

c 

Lorentz Velocity Transformation
see page 40
dx   dx ' vdt'
dy  dy '
dz  dz '
dx ' 

dt    dt ' 

c 

dx
 dx'vdt'
ux 

dx' 
dt

  dt ' 

c 

dy
dy '
uy 

dx' 
dt

  dt ' 

c 

Lorentz Velocity Transformation
see page 40
ux 
dx
 dx'vdt'

dx' 
dt

  dt ' 

c


 dx' 
 v
 dt '


  dx' 
 dt ' 1 

c
dt
'


 dt ' 
 dy ' 
dt ' 

dy
dy '
dt
'


uy 


dx' 
dt

  dx' 
  dt ' 

dt
'

1 

c
c
dt
'





u ' x v
1


u'x
c
u' y


 1 


u'x 
c

Note that because of the time transformation, the y- and z-components get messed up.
A spaceship traveling at 60%c shoots a proton
with a muzzle speed of 99%c at an asteroid.
What is the velocity of the proton as viewed from a ‘stationary’ space station?
MISC. LORENTZ
TRANSFORMATION
EXAMPLES
Cosmic Ray Muon Lifetime
electron mo=9.1e-31 kg
halflife = inf
muon mo=207 * (mass e)
halflife = 1.5e-6 sec
http://landshape.org/enm/cosmic-ray-basics/
http://www.windows2universe.org/physical_science/physics/
atom_particle/cosmic_rays.html
Cosmic Rays
Susan Bailey
Nuclear News
Jan 2000, pg 32
Cosmic Ray references
Cosmic Ray Muon Measurements
http://www.youtube.com/watch?v=yjE5LHfqEQI
http://www.ans.org/pubs/magazines/nn/docs/2000-1-3.pdf
http://pdg.lbl.gov/2011/reviews/rpp2011-rev-cosmic-rays.pdf
http://hyperphysics.phy-astr.gsu.edu
ashsd.afacwa.org/
radation
cosmic rays
Cosmic Ray Muon Lifetime
Suppose muon traveling at 0.98c
muon mo=207 (9.1e-31 kg)
halflife = 1.5e-6 sec
Q1. Classically, how far could the muon travel
during a time 1.5e-6 sec ?
Q3. How far do we observe the muon
to travel during that time ?
Q4. How high does the muon think
the mountain is?
2000 meters
Q2. What do we observe the lifetime to be ?
Simultaneity
• http://www.youtube.com/watch?v=wteiuxyqtoM
• http://www.youtube.com/watch?v=KYWM2oZgi4E
Atomic Clock Measurements
• http://www.youtube.com/watch?v=cDvmN_Pw96A
• d
Twin Paradox
Video Clip
http://www.youtube.com/watch?v=A0jiY-CZ6YA
What’s the correct explanation of the paradox?
Reliable Discussion at
http://www.phys.unsw.edu.au/einsteinlight/jw/module4_twin_paradox.htm
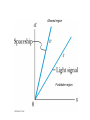
Spacetime Diagrams
Minkowski Diagrams
t
In SP211 course:
x
t
x
Allowed region
Forbidden region
Two events plotted on a space time diagram
P=(x,y,z,t)
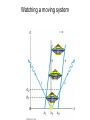
Simultaneity in a Stationary System
#1 Measuring location
#2 Measuring location
Watching a moving system
Animated Minkowski Diagrams
• http://www.youtube.com/watch?v=C2VMO7pcWhg
– (uses Minkowski space diagrams, but with time axis pointing
down, opposite from figures in textbook.)
Analysis of the
Twin Paradox
using
Minkowski Diagrams
Frank sends a signal once a year.
Mary sends a signal once a year.
Invariant Quantities
Define s2 = x2 – (ct)2
Then can show s’2 = x’2 – (ct’)2  x2 – (ct)2 = s2
 s2 is independent of choice of reference frame.
We can use s2 to discuss the ability for ‘events’
to impact one another.
s2 = x2 – (ct)2
If s2 < 0
then x2 < (ct)2 = c2 t2
The distance between ‘events’ is less than
the time required for light to propagate
between the spatial locations.
RELATIVISTIC MOMENTUM
Style 1. Sandin’s Development
Style 2. Rex & Thorton’s Development
The following 4 slides present
Sandin’s treatment of momentum
in Special Relativity
Forces and Momentum (Sandin version)
- a first look
u’x , u’y , u’z
v
ux 
p’x , p’y , p’z
mo
uy 
ux , uy , uz
u 'x v
1

c
v
u'x
u' y
 

 1  u ' x 
c



px , py , pz
If want p to ‘look like’ “mv” ;
mu y  mou ' y
1 
m u ' y   mo u ' y


Then are forced to let
m   mo
BUT
1

u' y
Forces and Momentum (Sandin version)


Ftot  ma
Suppose F ┴ u


dp
Ftot 
dt

d mu 
du dm
Ftot 
m

u
dt
dt dt
speed  const    const
 m  mo doesn' t change

dm
0
dt
du
du
F m
 mo
 mo a  ma
dt
dt
So why are we complaining about the phrase ‘relativistic mass’?
Forces and Momentum (Sandin version)


Ftot  ma
Suppose F || u


dp
Ftot 
dt

d mu 
du dm
Ftot 
m

u
dt
dt dt
speed  const    const



dm d
d
2 1 / 2

 m 
1 
m  ...
dt dt
dt
du dm
F m

u  ...   3 ma
dt dt
BECAUSE Newton’s Eqn Motion is different depending on the direction of the force.
Forces & Momentum (Sandin version)
PRORelativistic Mass People
ANTIRelativistic Mass People
Definitions
m =  mo
p=mu
No such thing
p= mu
Newton’s Eqn of Motion
if F ┴ u
F=ma
with m mo
F=dp/dt
Newton’s Eqn of Motion
if F || u
F=ma
with m mo
but throw in an extra 2
F=dp/dt
The following 9 slides present
Rex & Thorton’s
treatment of momentum in
Special Relativity
2.11: Relativistic Momentum
Because physicists believe that the
conservation of momentum is fundamental,
we begin by considering collisions where
there do not exist external forces and
dP/dt = Fext = 0
Relativistic Momentum
Frank (fixed or stationary system) is at rest in system K holding a
ball of mass m. Mary (moving system) holds a similar ball in
system K that is moving in the x direction with velocity v with
respect to system K.
Relativistic Momentum
• If we use the definition of momentum, the
momentum of the ball thrown by Frank is
entirely in the y direction:
pFy = mu0
The change of momentum as observed by
Frank is
ΔpF = ΔpFy = −2mu0
According to Mary
• Mary measures the initial velocity of her
own ball to be u’Mx = 0 and u’My = −u0.
K’
In order to determine the velocity of Mary’s
ball as measured by Frank we use the
velocity transformation equations:
K
Relativistic Momentum
Before the collision, the momentum of Mary’s ball as
measured by Frank becomes
K
Before
Before
For a perfectly elastic collision, the momentum after the
collision is
After
K
After
(2.42)
(2.43)
The change in momentum of Mary’s ball according to Frank
is
(2.44)
Relativistic Momentum
 The conservation of linear momentum requires
the total change in momentum of the collision, ΔpF
+ ΔpM, to be zero. The addition of Equations (2.40)
and (2.44) clearly does not give zero.
 Linear momentum is not conserved if we use the
conventions for momentum from classical physics
even if we use the velocity transformation
equations from the special theory of relativity.
There is no problem with the x direction, but there
is a problem with the y direction along the direction
the ball is thrown in each system.
Relativistic Momentum
• Rather than abandon the conservation of linear
momentum, let us look for a modification of the
definition of linear momentum that preserves both
it and Newton’s second law.
• To do so requires reexamining mass to conclude
that:
Relativistic momentum (2.48)
Relativistic Momentum
 Some physicists like to refer to the mass in Equation
(2.48) as the rest mass m0 and call the term m = γm0
the relativistic mass. In this manner the classical form
of momentum, m, is retained. The mass is then
imagined to increase at high speeds.
 Most physicists prefer to keep the concept of mass
as an invariant, intrinsic property of an object. We
adopt this latter approach and will use the term mass
exclusively to mean rest mass. Although we may use
the terms mass and rest mass synonymously, we will
not use the term relativistic mass. The use of
relativistic mass to often leads the student into
mistakenly inserting the term into classical expressions
where it does not apply.
RELATIVISTIC KINETIC ENERGY
The following 5 slides present
Rex & Thorton’s
treatment of kinetic energy
in Special Relativity
2.12: Relativistic Kinetic Energy
Newtonian KE=1/2 m u2 which came from
KE = Work = ∫ F•ds with F = dp/dt = m dv/dt = ma
Relativistic Kinetic Energy
Start from rest and accelerate until u
Integration by parts
 u dv  uv   v du
Relativistic Kinetic Energy
Start from rest and accelerate until u
Integration by parts
 u dv  uv   v du
u
KE  m u u  m  u du
0

u du
1 u c 
1/ 2
2
 c2 
2
 d
1   
2 1/ 2
 c 2 1   2
imits
evaluate

 mc2 1  u
KE  mu 
2
1
2
mc2  mc2
2
c
2
 mc2
Relativistic Kinetic Energy
KE  mu 
2
1

2
mc  mc
2
2
 


2
 2 1 2
2
2
2
2
2
u
u  c   u  2 c    u  1 
c


u

c

u
2
c




2
1
2
KE  mc  mc
2
KE    1 mc

2
2
Which reduces to the Newtonian expression for u small
Comparison
Relativistic and Classical Kinetic Energy
Formula
Relativistic
Kinetic
Energy
Equation (2.58) does not seem to resemble the classical result for kinetic energy, K
= ½mu2. However, if it is correct, we expect it to reduce to the classical result for low
speeds. Let’s see if it does. For speeds u << c, we expand in a binomial series as
follows:
where we have neglected all terms of power (u/c)4 and greater, because u << c.
This gives the following equation for the relativistic kinetic energy at low speeds:
(2.59)
which is the expected classical result. We show both the relativistic and classical
kinetic energies in Figure 2.31. They diverge considerably above a velocity of 0.6c.
Total Energy
KE    1 mc
2
KE   mc  mc
2
2
 mc  KE  mc
2
2
Tot Energy  Etot   mc
2
Relationship between
Total Energy & Momentum
p   mu
Square, mult c2, convert u, use =(1-2)1/2 to subst 4 
p c  m c m c
2 2
2
2 4
2 4
p c  E m c
2 2
2
tot
2 4
E p c m c
2
tot
2 2
2 4
an invariant
Youtube clips (part 3)
• Galilean/Classical Relativity
Part 3 – The Cassiopeia Project
http://www.youtube.com/watch?v=W6o_-yTa168
The Cassiopeia Project is an effort to make high quality science videos available to everyone.
If you can visualize it, then understanding is not far behind.
http://www.cassiopeiaproject.com/
To read more about the Theory of Special Relativity, you can start here:
http://www.phys.unsw.edu.au/einsteinlight/
http://www.einstein-online.info/en/elementary/index.html
http://en.wikipedia.org/wiki/Special_relativity
Examples
Example 2.11
mc2 = 0.511 MeV
m = 9.1e-31 kg
|q| = 1.6e-19 Coul
Electrons in a television set are accelerated by a
potential difference of 25000 Volts before striking the
screen.
a). Calculate the speed of the electrons and
b). Determine the error in using the classical kinetic
energy result.
http://express.howstuffworks.com/exp-tv1.htm
http://www.o-digital.com/wholesale-products/2227/2285-4/LCD-TV-LDT32-225837.html
Example 2.13
A 2-GeV proton hits another 2-GeV proton in a head-on collision in
order to create top quarks.
http://www.fnal.gov
• For each of the initial protons, calculate
– Speed v
– 
– Momentum p
– Rest-mass Energy
– Kinetic Energy KE
– Total Energy Etot
mc2=938 MeV
Example 2.16
The helium nucleus is built from 2 protons and 2 neutrons.
The binding energy is the difference in rest mass-energy of
the nucleus from the total rest mass-energy of it’s
component parts.
Calculate the nuclear binding energy of helium.
mHe = 4.002603 amu
mp = 1.007825 amu
mn = 1.008665 amu
Hints:
1 amu = 1.67e-27 kg
or
c2 = 931.5 MeV/amu
http://www.dbxsoftware.com/helium/
Example 2.17
The molecular binding energy is called dissociation energy.
It is the energy required to separate the atoms in a molecule.
The dissociation energy of the NaCl molecule is 4.24 eV.
Determine the fractional mass increase of the Na and Cl
atoms when they are not bound together in NaCl.
mNa = 22.98976928 amu
Average mCl = 35.453 amu
http://www.ionizers.org/water.html
Hints:
1 amu = 1.67e-27 kg
or
c2 = 931.5 MeV/amu
Sandin 5.30
A spaceship has a length of 100 m and a mass of 4e+9 kg
as measured by the crew. When it passes us, we measure
the spaceship to be 75 m long.
What do we measure its momentum to be?
RHIC
The diameter of an gold nucleus is 14 fm.
If a Au nucleus has a kinetic energy of 4000 GeV, what is the
apparent ‘thickness’ of the nucleus in the laboratory?
Length contraction
mc2=197*931.5 MeV
http://www.bnl.gov/rhic/
Sandin 5.22
At the Stanford Linear Accelerator, 50 GeV electrons are produced
• For one of these electrons, calculate
– Speed v
– 
– Momentum p
– Rest-mass Energy
– Kinetic Energy KE
– Total Energy Etot
http://www.flickr.com/photos/kqedquest/3268446670/
http://www.daviddarling.info/encyclopedia/L/linear_accelerator.html
mc2 = 0.511 MeV
Sandin 5.25
A cosmic ray pion (rest mass 140 MeV/c2) has a momentum of 100 MeV/c.
http://www.mpi-hd.mpg.de/hfm/CosmicRay/Showers.html
• Calculate
– Speed v
– 
– Momentum p
– Rest-mass Energy
– Kinetic Energy KE
– Total Energy Etot
http://www2.slac.stanford.edu/vvc/cosmicrays/cratmos.html
Sandin 4.26
Spaceship A moves past us at 0.6c
followed by Spaceship B in the same direction at 0.8c
B
What do they measure as their relative speed of approach?
What do we measure as their relative speed of approach?
A
Sandin 4.28
Spaceship A approaches us from the right at at 0.8c
Spaceship B approaches us from the left at 0.6c
B
A
What do they measure as their relative speed of approach?
What do we measure as their relative speed of approach?