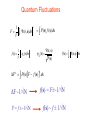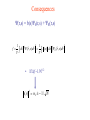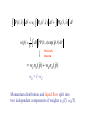* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download pisa lecture 3
Scalar field theory wikipedia , lookup
Bohr–Einstein debates wikipedia , lookup
Canonical quantization wikipedia , lookup
Copenhagen interpretation wikipedia , lookup
Quantum state wikipedia , lookup
Orchestrated objective reduction wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Renormalization group wikipedia , lookup
Wave function wikipedia , lookup
Hidden variable theory wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Wave–particle duality wikipedia , lookup
Matter wave wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Lecture 3 BEC at finite temperature Thermal and quantum fluctuations in condensate fraction. Phase coherence and incoherence in the many particle wave function. Basic assumption and a priori justification Consequences Connection between BEC and two fluid behaviour Connection between condensate and superfluid fraction Why BEC implies sharp excitations. Why sf flows without viscosity while nf does not. How BEC is connected to anomalous thermal expansion as sf is cooled. Hoe BEC is connecged to anomalous reduction in pair correlations as sf is cooled. Thermal Fluctuations f (T ) j (T ) F j At temperature T j Boltzman factor exp(-Ej / T)/Zj 2 1 F j n j (0) ds j (r , s )dr V f j (T ) F j f 2 2 j Δf ~1/√N Fj = f ± ~ 1/ √ N Basic assumption; (√f is amplitude of order parameter) E g (E) (E)dE j j j g(E) All occupied states give same condensate fraction η(E) ΔE, Δf ~1/ √ N-1/2 Can take one “typical” occupied state as representative of density matrix E As T changes band moves to different energy “Typical” state gives different f All occupied states gives same f to ~1/√N Drop subscript j to simplify notation Quantum Fluctuations 1 F V (r, s)dr V 1 f (s) s (r )dr V V 2 P (s) f (s)ds S (r) (r, s) P(s) P(s) (r, s) dr F P(s)F f (s) ds 2 ΔF ~1/√N F = f ±~1/√N 2 f(s) = F±~1/√N f(s) ~ f ± 1/√N 2 V width~ħ/L BEC n(p) n(p) S (r) exp( ip .r )dr S (r) 2 Weight f to ~1/√N for any state and any s Delocalised function of r (non-zero within volume > f V) J. Mayers Phys. Rev. Lett. 84 314 (2000),Phys. Rev.B 64 224521, (2001) S(r ) Phase correlations in r over distances ~L otherwise S (r )dr ~ 0 Phase coherent Phase incoherent rC Condensate No condensate ~1/rC Temperature dependence At T = 0 , Ψ0(r,s) must be delocalised over volume ~ f0V and phase coherent. For T > TB occupied states Ψj(r,s) must be either localised or phase incoherent. What is the nature of the wave functions of occupied states for 0 < T < TB? BASIC ASSUMPTION Ψ(r,s) = b(s)Ψ0(r,s) + ΨR(r,s) • Ψ0(r,s) is phase coherent ground state • ΨR(r,s) is phase incoherent in r • b(s) 0 as T TB for typical occupied state • ΨR(r,s) 0 as T 0 1. 2. 3 4. Gives correct behaviour in limits T TB, T 0 True for IBG wave functions. Bijl-Feynman wave functions have this property Implications agree with wide range of experiments Bijl-Feynman wave functions J. Mayers, Phys. Rev.B 74 014516, (2006) (r , s ) (r , s )0 (r , s ) (r , s ) exp( ik . r ) n k n 1 N nk • nk = number of phonon-roton excitations with wave vector k. •M = total number of excitations • sum of NM terms. M nk k (r, s) b(s) R (r, s) b(s) is sum of all terms not containing r = r1 Phase coherent in r. Fraction of terms in b(s) is (1-M/N) as N M N Θ(r,s) is phase incoherent (T TB) M 0 Θ(r,s) is phase coherent (T 0) ΘR(r,s) is sum of terms containing r Phase incoherent in r rC ~1/Δk ~ 5 Å in He4 at 2.17K Consequences Ψ(r,s) = b(s)Ψ0(r,s) + ΨR(r,s) 2 1 1 f ds (r , s )dr V V 2 b(s) ds 0 (r , s)dr 2 • If Δf ~1/N1/2 2 b( s ) wC ~ 1 / N Microscopic basis of two fluid behaviour 2 2 2 (r , s ) dr wC 0 (r , s ) dr R (r , s ) dr X (s ) ~ 1/ N X (s ) 0 (r , s ) R (r , s ) X dr ~ 1 / Macroscopic System 2 2 2 (r , s ) dr wC 0 (r , s ) dr R (r , s ) dr N 2 2 2 (r , s ) dr wC 0 (r , s ) dr R (r , s ) dr 2 1 n( p) ds (r , s ) exp( ip.r )dr V Parseval’s theorem wC n0 ( p) wR nR ( p) wR = 1- wC. Momentum distribution and liquid flow split into two independent components of weights wC(T), wR(T). E wC E0 wR ER Thermodynamic properties split into two independent components of weights wc(T), wR(T) SC E0 T V 0 Bijl-Feynman wR determined by number of “excitations” wc(T) = ρS(T) wR(T) = ρN(T) • True to within term ~N-1/2 • Only if fluctuations in f, ρS and ρN are negligible. • Not in limits T 0 T TB f (T ) S (T ) f (0) f (T ) f (0) oo T. R. Sosnick,W.M.Snow and P.E. Sokol Phys. Europhys Lett 9 707 (1989). X X H. R. Glyde, R.T. Azuah and W.G. Stirling Phys. Rev. B 62 14337 (2000). E P S P0 N PN V T (T ) ( 0) Superfluid has extra “Quantum pressure” PN = PB 2 1 S (q ) i (r1 , s ) N 2 exp( iq.rn ) dr1ds S S 0 (q ) N S R (q ) S (q ) 1 S R (q ) 1 SR-1 S N 1 q S-1 (T ) 1 S (T )[1 0 ] α < 1 → S less ordered than SR V.F. Sears and E.C. Svensson, Phys. Rev. Lett. 43 2009 (1979). α(T) α0 (T ) 1 S (T )[1 0 ] SR(q) S0(q) → Ψ0(r,s) and ΨR(r,s) 0 for different s Why is superfluid more disordered? For s where Ψ0(r,s) 0 ~7% free volume Assume for s where ΨR(r,s) 0 negligible free volume Ground state more disordered Quantitative agreement with measurement at atomic size and N/V in liquid 4He J. Mayers Phys. Rev. Lett. 84 314 (2000) Phase coherent component Ψ0(r,s) s such that Ψ0(r,s) is connected (r ).dr 2n (Macro loops) Quantised vortices, macroscopic quantum effects Phase incoherent component ΨR(r,s) s such that ΨR(r,s) is not connected Localised phase incoherent regions. Localised quantum behaviour over length scales rC ~ 5 Å No MQE or quantised vortices Excitations S (q, ) 1 N 2 A f (q) ( E E f ) f Momentum transfer = ħq Energy transfer = ħω A f (q) N * (r, s) f (r, s) exp( iq.r )drds |Aif(q)|2 has minimum width Δq ~ 1/rC Phase incoherent Regions of size ~rC Normal fluid - momentum of excitations is uncertain to ~ ħ/rC Superfluid - momentum can be defined to within ~ ħ/L 0 < T < TB ε ( deg K) h/rC q (Å-1) Anderson and Stirling J. Phys Cond Matt (1994) Landau Theory Basic assumption is that excitations with well defined energy and momentum exist. Only true in presence of BEC Landau criterion vC = (ω/q)min Normal fluid vC = 0 ω q Summary BASIC ASSUMPTION Ψ(r,s) = b(s)Ψ0(r,s) + ΨR(r,s) Phase coherent ground state • Has necessary properties in limits T0, T TB • IBG, Bijl-Feynman wave functions have this form •Simple explanations of •Why BEC is necessary for non-viscous flow Why Landau theory needs BEC. Phase incoherent Summary Existing microscopic theory does not provide even qualitative explanations of the main features of neutron scattering data This is the only experimental evidence of the microscopic nature of Bose condensed helium. Theory given here explains quantitatively all these features Why the condensate fraction is accurately proportional to the superfluid fraction Why spatial correlations decrease as superfluid helium is cooled Why superfluid helium is the only liquid which contains sharp excitations Why superfluid helium expands when it is cooled