Download Lock-in amplifiers

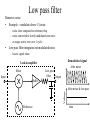
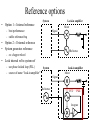
Lock-in amplifiers
http://www.lockin.de/
Signals and noise
Frequency dependence of noise
• Low frequency ~ 1 / f
Total noise in 10 Hz bandwidth
– example: temperature (0.1 Hz) , pressure
(1 Hz), acoustics (10 -- 100 Hz)
– example: shot noise, Johnson noise,
spontaneous emission noise
• Total noise depends strongly on signal freq
– worst at DC, best in white noise region
• Problem -- most signals at DC
log(Vnoise)
• High frequency ~ constant = white noise
Signal at DC
1/f noise
10 Hz
White noise
0
0.1 1
10 100 1kHz
log( f )
Noise amplitude
Signal at 1 kHz
log(Vnoise)
White noise
log(Vnoise)
1/f noise
1/f noise
White noise
10 Hz
0
0
0.1 1
10 100 1kHz
log( f )
0.1 1
10 100 1kHz
log( f )
Lock-in amplifiers
• Shift signal out to higher frequencies
• Approach:
• Modulate signal, but not noise, at high freq
– no universal technique -- art
– example: optical chopper wheel, freq modulation
• Detect only at modulation frequency
– Noise at all other frequencies averages to zero
– Use demodulator and low-pass filter
Demodulation / Mixing
•
•
•
•
Multiply input signal by sine wave
Sum and difference freq generated
Compare to signal addition -- interference
Signal frequency close to reference freq
– low freq beat
– DC for equal freq sine waves
– DC output level depends on relative phase
Product
Two sine waves
Sum
Signal freq approaches ref freq
• Beat frequency approaches DC as signal freq approaches ref freq
Reference
Signal freq
vs ref freq
Mixer outputs
1
1.05
1.1
1.15
1.2
1.25
Phase sensitive detection
• Signal freq matches reference freq
• Reference = sin(2pft)
• Signal = sin(2pft + f)
– f is signal phase shift
• Product = cos(f) - cos(2pft)
DC part
Product waveforms
-- signal times reference
Reference wave
Signal
phase
shift f
0
0.2 p
0.4 p
0.6 p
0.8 p
p
Low pass filter
Removes noise
• Example -- modulate above 1/f noise
– noise slow compared to reference freq
– noise converted to slowly modulated sine wave
– averages out to zero over 1 cycle
• Low pass filter integrates out modulated noise
– leaves signal alone
Demodulated signal
Lock-in amplifier
Mixer
After mixer
Low pass
filter
Output
Input
Buffer
Voltage
After mixer & low pass
Reference
time
Typical LIA low pass filters
• For weak signal buried in noise
• Ideal low pass filter blocks all except signal
• Approximate ideal filter with cascaded low pass filters
Ideal
6 db/oct
12 db/oct
log
gain
18 db/oct
frequency
Phase control
•
•
•
•
Reference has phase control
Can vary from 0 to 360°
Arbitrary input signal phase
Tune reference phase to give maximum DC output
Mixer
Input
Output
Reference
Phase
shift f
Reference options
• Option 1 -- Internal reference
System
Lock-in amplifier
Mixer
– best performance
– stable reference freq
Signal
• Option 2 -- External reference
• System generates reference
Reference
– ex: chopper wheel
• Lock internal ref to system ref
– use phase locked loop (PLL)
– source of name “lock-in amplifier”
System
Lock-in amplifier
Mixer
Signal
Reference
VCO
PLL
Integrate
Analog mixer
• Direct multiplication
Multiplying mixer
– accurate
– not enough dynamic range
– weak signal buried in noise
• Switching mixer
– big dynamic range
– but also demodulates harmonics
Harmonic content of square wave
1
1/3
1/5
1/7
1/9
Switching mixer
Switching mixer design
• Sample switching mixer
• Back-to-back FETs
– example: 1 n-channel & 1 p-channel
– feed signal to one FET, inverted signal to second FET
• Apply square wave to gates
– upper FET conducts on positive part of square wave
– lower FET conducts on negative part
Switching mixer circuit
n-channel FET
bias
source
drain
gate
n
p
Signal
voltage
Signals with harmonic content
• Option 1: Use multi-switch mixer
– approximate sine wave
– cancel out first few harmonic signals
• Option 2: Filter harmonic content from signal
– bandpass filter at input
– Q > 100
Lock-in amp with input filter
Digital mixers
• Digitize input with DAC
• Multiply in processor
• Advantages:
– Accurate sine wave multiplication
– No DC drift in low pass filters
– Digital signal enhancement
• Problems:
– Need 32 bit DAC for signals buried in noise
– Cannot digitize 32 bits at 100 kHz rates
• Should be excellent for slow servos
– Ex: tele-medicine, temperature controllers
– Digital processing can compensate for certain system time delays ?
Lock-in amps in servos
•
Lock to resonance peak
– Servos only lock to zero
– Need to turn peak into zero
•
Take derivative with lock-in
Take derivative of lineshape
– modulate x-voltage
– F(x)-voltage amplitude like derivative
•
No fundamental
• only 2 f signal
Use lock-in amp to extract amplitude of F(x)
– “DC” part of mixer output
– filter with integrator, not low-pass
F(x)
x
Lock-in amps for derivative
• Lock-in turns sine wave signal into DC voltage
• At peak of resonance
– no signal at modulation freq
– lock-in output crosses zero
Input signal
• Discriminant
– use to lock
F(x)
x
Zero crossing
at resonance
Lock-in
output
(derivative)
Effect of modulation on lineshape
• Start with resonance lineshape
• Intensity vs PZT voltage: I = I0 exp( -V2)
I
V
• Modulate voltage: V= V0 sin (2 p f t)
V
• Modified lineshape
t
• Analog to numerical derivatives
• Derivative is: I’ = I(V+ DV) - I(V) / DV
– Set DV = 1
• Modulation replaces DV= V0 sin (2 p f t)
• Derivative is sine wave part
I
– Assumes is V0 small
t
Effect of modulation amplitude
•
For large modulation amps
Modulation amplitude
– Distortion and broadening
•
Modulation like a noise source
0.05 linewidth
– Always use minimum necessary
0.1
0.2
0.5 linewidth
1
2
Expanded scan
Mixer outputs
Modulation amplitude
• Maximum mixer output
– modulation ~ 1 linewidth
– saturates and broadens
0.1 linewidth
0.2
0.5 linewidth
1
2
Mixer out
0.1 linewidth
0.2
0.5
1
2
Fabry-Perot servo
• Lock to peak transmission of high Q Fabry-Perot etalon
• Use lock-in amp to give discriminant
– No input bandpass -- or low Q < 2
• Bandpass rolloff usually 2-pole or greater
– No low pass filter -- replace with integrator
• Low pass filter removes noise
• Need noise to produce correction
• Design tips
– reference freq must exceed servo bandwidth by factor of ~ 10
– but PZT bandwidth is servo limiter
– use PZT resonance for modulation
Fabry-Perot
Laser
PD
Acoustic noise
LIA
reference
Sum
& HV