Download Week 7 2010

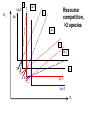
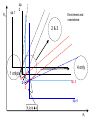
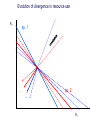
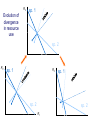
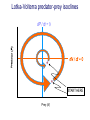
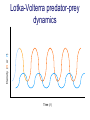
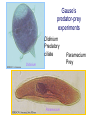
Resource competition
among >2 species
• One resource
– species with lowest R* excludes all others
– example: species 1 excludes all others
Resource competition
among >2 species
• Two resources, essential
• Constant, homogeneous environment
• Two resources - two coexisting species
at equilibrium
– which two species depends on resource
ratios
– each species is best competitor for a
particular ratio of resources
1
R2
1&2
sp.2
sp.1
Resource
competition,
>2 species
2
2&3
3
3& 4
2
4
13
24
3
sp.3
sp.4
R1
New effect: spatial variation
• Suppose resource ratios vary locally
– natural heterogeneity in soil nutrients
– consequences for coexistence?
• When there is local spatial variation in
resource ratios, >2 species can coexist
– with local spatial segregation (patchiness)
– More species than resources
R2
Variation in
resource ratios
sp.2
sp.1
2
13
24
3
sp.3
sp.4
R1
Spatial variation
•
•
•
•
Local variation fosters diversity
More species than resources possible
Dependent on extent of variation
Plant communities
– often 100’s or 1000’s species
– only about 12 essential resources
– often patchy
• Variance in Resource Ratios Hypothesis (VRR)
What is the effect of
nutrient enrichment?
• Relationship of diversity & productivity
• Unimodal vs. Monotonic
• Mechanisms producing relationships
– Unimodal
– particularly decrease in diversity with
productivity
R2
sp.1
sp.
2
Enrichment and
coexistence
2&3
4 only
1 only2
13
24
3
sp.3
sp.4
R1
Nutrient enrichment
• Increase all resources uniformly
– local variation in resource ratios allows coexistence
of fewer species
• Increase one resource
– necessarily makes resource ratios more extreme
– raises, then lowers number of coexisting species
• Assumes resources increase without
increasing variation
• “Paradox of enrichment”
– enrichment = reduced diversity
Switching resources
• Does VRR predict coexistence of many
species on 2 switching resources?
– species don’t specialize on ratios
– each species consumes one resource or the other
only
• At equilibrium there are 2 species, each
consuming and limited by one resourse
– Fundamental difference between animal and plant
communities
Switching
resources
R2
sp.4
1&4
sp.3
sp.
2
4
sp.1
1
R1
Plants vs. Animals
• Plants use essential resources
• VRR predicts high species:resources
ratio
• Animals use switching resources
• Theory predicts species:resources ratio
=1
Coexistence and evolution
• Competitive coevolution
–
–
–
–
2 spp. competing for 1 resource cannot coexist
if individuals vary in resource use
if that variation is heritable
competition creates selection
• May select for increasing efficiency
– selection for better resource use (lower R* )
– a “race” to be most efficient
– end result is still exclusion
Coexistence and evolution
• Competition may select for divergence in
resource use
– individuals exploiting an alternative resource
favored (not affected by competition)
– alternative resources could be different spatially,
temporally, in size
– for substitutable or switching resources
– evolution of divergence may avoid exclusion
Example: Divergence in prey size
freq. of use
selection against
time
freq. of use
size of prey
size of prey
Evolution of divergence in resource use
R2
sp. 1
sp. 2
sp. 2
sp. 1
R1
R2
Evolution of
divergence
in resource
use
sp. 1
sp. 2
R2
R2
sp. 1
sp. 2
sp. 1
sp. 2
R1
Competitive character
displacement
• Competition selects for divergence in a
morphological feature
– presumably results in divergence of
resource use
– often held to be the best evidence for the
importance of competition
– Example: Sitta nuthatches
Nuthatches
– Example: Sitta nuthatches
– Asia & Europe
– Ranges include regions of allopatry (no
contact)
– also regions of sympatry (co-occur)
– Sitta neurenmayer (Europe)
– Sitta tephronata (Asia)
– Sympatry in Iran
Nuthatches
• Bill size
– related to prey size
– data suggest character displacement on bill
size
•
S. neurenmeyer
tephronta
• Allopat.
25 mm
• Sympat.
22 mm
S.
25 mm
28 mm
Prediction of character displacement
bill length (mm)
S. tephronata
S. neurenmayer
site (longitude)
Actual pattern (Grant 1972)
bill length (mm)
S. tephronata
S. neurenmayer
site (longitude)
Nuthatches
• No shift in cline of bill size when region of
sympatry is reached
• Bill sizes vary geographically in a
continuous fashion
• Not much evidence for character
displacement
Hydrobia snails
• intertidal mud snails
– particle feeders (diatoms, sediment)
• Allopatry
– H. ventricosa
– H. ulvae
mean length = 3.1 mm
mean length = 3.3 mm
• Sympatry
– H. ventricosa
– H. ulvae
mean length = 2.8 mm
mean length = 4.5 mm
Hydrobia snails
Questions
• Character displacement?
• Competition for food particles?
• Levinton - does particle size affect
growth?
– larger species does best on larger
particles?
• Result: No difference in growth for
different particle sizes
Hydrobia snails: More questions
• H. ulvae & H. ventricosa sympatric in lagoons
• H. ulvae alone in intertidal
• Lagoon H. ulvae
– alone … 1.2 X larger than intertidal H. ulvae
– w/ H. ventricosa … 1.4 X larger than intertidal H.
ulvae
• size difference due to physical environment?
• lagoons: low reproduction, high growth
Character displacement
• Classic cases of character displacement now
questioned
• Probably not a widespread phenomenon
• Morphology (size) presumed related to resource
use
• Competition presumed to be the driving force
• Examples of size differences reducing
competition?
Caribbean Anolis
Pacala & Roughgarden 1985
• St. Maarten
• A. gingivinus
– SVL = 41 mm
• A. wattsi
– SVL = 38 mm
• St. Eustatius
• A. bimaculatus
– SVL = 53 mm
• A. wattsi
– SVL = 40 mm
Caribbean Anolis
• Predict less competition on St. Eustatius
• Note: size strongly correlated with prey
size
Experiment
12 X 12 m enclosures; fenced 1.5 m; clear lizards
60 Ag
100 Aw
60 Ag
60 Ab
100 Aw
60 Ab
60 Ag
100 Aw
60 Ag
60 Ab
100 Aw
60 Ab
St. Maarten
St. Eustatius
Caribbean
Anolis
• St. Maarten
• A. gingivinus + A. wattsi
– less food in stomach
– lower growth rate (0.5X)
– perch height higher (2X)
• St. Eustatius
• A. bimaculatus + A. wattsi
– same amount in stomach
– same growth rate
– same perch height
• compared to A. gingivinus • compared to A. bimaculatus
alone
alone
• Interspecific effect strong • Interspecific effect absent
Alternative interpretation
• Suppose competition is absent on St. Eustatius
– large resource base, abundant food
– predators reduce density
• A. bimaculatus enclosures
– escapes occurred over time
– density:
60

45

30 lizards
–
1 mo
2 mo
– as density drops growth increases; competition
Conclusion
• Size difference  reduced competition
• One case, but it shows this effect is possible
• Authors do NOT claim size difference evolved
due to competition
• Has not established that size would evolve in
response to competition
Morphological evolution &
competition (Schluter 1994)
Sticklebacks
• species complex
• extreme body forms
Representative limnetic (top) and benthic (bottom) stickleback from Lake
Enos in British Columbia, Canada. Click to enlarge. Posted with permission
from Paul J. B. Hart and Andrew B. Gill, "Evolution of Foraging Behaviour
int the threespine stickleback," in The Evolutionary Biology of the
Threespine Stickleback, eds. Michael A. Bell and Susan A. Foster, (Oxford:
Oxford University Press), 1994, p. 211. © Oxford University Press
– limnetic - feed on plankton (e.g., Daphnia)
– benthic - feed on benthic invertebrates
see also Robinson & Wilson 1994
Sticklebacks
• Morphological intermediates exist
• 1 sp. in a lake -- typically intermediate
morph
• 2 spp. in a lake -- typically 2 morphs
• Morphology is related to feeding
efficiency and growth
• Hypothesis: evolved morphological
divergence due to competition (Character
displacement)
Experiment
• 23 X 23 m ponds
• Target species intermediate in morphology
• produced by hybridization
intermediate X intermediate
intermediate X limnetic
intermediate X benthic
Morphology
Hypothesis
• Competition with a limnetic will have greatest
effect on survival and growth of forms
morphologically similar to limnetic
Target
Limnetic
Morphology
Target
Limnetic
Morphology
Experiment
• Hybrids add variation on which selection
can work
intermediate X intermediate
intermediate X limnetic
intermediate X benthic
Morphology
Implication
• If hypothesis is supported, selection for
character divergence is occurring via
competition
Experiment
Experimental
1800 target
1200 limnetic
Control
1800 target
X 2 ponds
Data collection
• 3 months
• Collect fish, measure Target
• Growth rate reduced by density
– competition occurs
• Regression of growth vs. morphology
• Slope = growth differential between
more benthic and more limnetic
Results
Control
Competitor
IxB
IxI
IxL
morphology
Results
• Growth differential
– significant for 1 experimental group
– nearly so for a 2nd experimental group
– clearly not significant for both controls
• Survival differential
– some evidence for an effect in 1 pond
• Target individuals with limnetic
morphology fare worst
Conclusions
• Experimental evidence for character
displacement
• Caveats:
– pseudoreplication
– statistical weakness
Lake whitefish
Coregonus lavaretus
dwarf, limnetic
benthic
Null models in
community ecology
• Experiments
– show that a process occurs
– may show it can cause effects on distribution,
abundance, fitness of a limited set of species
– Does that process structure the community as a
whole?
– experiments rarely can test that
• If interspecific competition is important, what
patterns would be predicted for communities?
Community patterns
• Competition favors differences in resource
use among co-occurring species
• Predict: co-occurring species should be
more different in resource use than expected
if species were placed together randomly.
• Should be present across similar species
within a community
G. E. Hutchinson
• Co-occurring European Corixids
• Body lengths – ratio of larger to
smaller tended to be >1.3
• Morphology as a surrogate for
resource use
• Origin of idea of limiting
similarity
Morphological pattern
• Predict: co-occurring species should be more
different in morphology than expected if species
were placed together randomly.
• "Community-wide character displacement"
• How do you tell?
• Null models or Neutral models of communities
• Morin 98-103; Chase & Leibold 117-122
Statistical Null hypotheses
• Hypothesis of only chance affecting outcome
• e.g., c2 for mendelian assortment
– coat color… Red
–
RR
•
•
•
•
White
rr
Roan
Rr
Cross two Roan: Rr x Rr
Expect:
RR = 0.25; Rr = 0.50; rr = 0.25
observe: RR = 0.26; Rr = 0.38; rr = 0.36
c2 = 7.76, P<0.05 … significant departure from
(null) expectation
Statistical Null hypotheses
• Expected: assumption of random sampling of
alleles
• P<0.05: results deviating as far (or farther) than
observed expected <5% of the times if only
random processes are involved
• conclude: some non-random process is
structuring alleles at this locus
• Same general pattern in community ecology,
but the model and math are more complex
Example – Dytiscid beetles
•
•
•
•
(Juliano & Lawton 1990)
28 species, Northern England
9 different sites have 8 to 16 species
interspecific variation in size and shape
Are co-occurring species more different in
morphology than expected?
Hyphydrus ovatus
Hygrotus
inaequalis
Hydroporus planus
Issues for null models
• What is the character of interest?
– Resource use
– Morphology
• one variable
• many variables
• correlation of variables
– Co-occurrence (do pairs of species co-occur
less often than expected … “forbidden
combinations”)
Issues for null models
• What is the source pool of species?
– Islands
• Mainland fauna
• All species on similar islands
– Limits of source pool
• Taxonomic
• Geographic
• Trophic
Issues for null models
• What is the source pool of species?
– Real species (discrete values)
• Randomization tests
– Statistical distributions (continuous)
• Monte Carlo methods; simulations
Issues for null models
• Identifying the assemblage present
– presence/absence
– abundance
• rare species may transients, not integrated
into the community
• rarity may be a result of inappropriate
morphology or resource use
Issues for null models
• Test statistic – measure of differences
– Size ratios (Univariate only)
– Morphological nearest neighbor distance
– Minimum spanning tree
• Mean vs. Variation
– predict mean difference larger than expected
– predict variation of difference smaller than
expected (regularity of species spacing)
– combination
Issues for null models
• Constraints on randomization
– Stratify by other factors, e.g., genera within
families
– Overall distribution – widespread species more
likely to be included
– Dispersal ability – good dispersers more likely
to be included
Source pool : The narcissus effect
• Colwell & Winkler 1984
• What if assemblages at all locations are affected
by competition
– morphologies are more distinct than expected
– randomly draw real species … that effect is
incorporated into randomly drawn assemblages
– real assemblages do not differ from randomly drawn
because both include the effect of competition on
morphology
Source pool issues: The narcissus effect
# species
# species
• Solution?
• Synthetic species (unlike any real species, but
within the range of variation)
• Draw from continuous distributions of
morphological variables (match discrete
distributions)
size
size
Dytiscid morphology
• length, width, depth, head width
– correlated in real species
• for real species, choose at random, and allocate to
community
– each species brings correlated morphological measurements
• Cannot simply choose length, width, depth, head
– omits correlation structure
• Canonical discriminant function
– produces uncorrelated variables (up to 4)
– choose canonical variates
Dytiscid
beetles
Test: randomization
• real community with S species
– calculate nearest neighbor distance
(NND) in morphological space for
all species
– get mean NND and SD NND
• draw S species from pool
– calculate NND in morphological space for all species
– get mean NND and SD NND
• Repeat many (500 or 1000) times
• Test stat [Mean NND – SD NND] =D
• Is real D large compared to those drawn at random?
Test: Monte Carlo
• real community with S species
– calculate nearest neighbor distance (NND) in morphological
space for all species
– get mean NND and SD NND
• draw S species from distributions of Canonical functions
– calculate NND in morphological space for all species
– get mean NND and SD NND
• Repeat many (500 or 1000) times
• Test stat [Mean NND – SD NND] =D
• Is real D large compared to those drawn at random?
Test statistic
• Reject H0 if observed >95% of all others
• Result …For one site, there was a significant pattern
of large mean NND and large D, but not of small SD
NND
• Species at one site are more dissimilar than expected
by chance
– and given average dissimilarity, the are less variable than
expected by chance (D)
• using synthetic species (vs. real) null hypothesis is
rejected slightly more frequently (narcissus effect)
Real species
Synthetic species
Null distribution
and real
communties
Other results
• Significant
– Hawks (Accipter spp.)
– Middle eastern cats
– Some tiger beetle
(Carabidae)
assemblages
– Desert Rodents
• Not significant
– Birds (Tres Marias &
Channel Islands)
– Most tiger beetle
assemblages
– Multiple passerine bird
assemblages
What does it show?
• A significant result establishes that there is a
pattern, consistent with prediction.
• Does not establish what the mechanism is.
• Experiments to test mechanisms where patterns
exist
– e.g., experiments like Pacala & Roughgarden
Exploitation
mostly predation
Exploitation
mostly predation
• Predator: kills and eats victim
• Parasite: lives intimately with victim and
usually does not necessarily kill victim
• Herbivore/Carnivore distinction not that
important for dynamics
Exploitation
• How does the presence / absence of a
predator affect:
– species populations
– assemblages of prey species
– evolution of prey
• Does predation contribute to community
patterns?
Predation & population dynamics
•
•
•
•
•
•
Predators eat prey; prey die due to predation
How does this affect population dynamics?
Lotka-Volterra predator-prey model
Starting point
N = number in prey population
P = number in predator populatio
Lotka-Volterra predator-prey
• Without predation, prey grow exponentially
dN / dt = r1 N
•
•
•
•
Predation is an increasing function of N & P
Effect of predation on prey population = C1 NP
C1 is the capture efficiency
So, with predation…
dN / dt = r1 N - C1 NP
Lotka-Volterra predator-prey
• Without prey, predators starve to death
exponentially
dP / dt = - r2 P
•
•
•
•
Predation is an increasing function of N & P
Effect of predation on predator population=C2 NP
C2 = product of capture & conversion efficiencies
So, with prey …
dP / dt = C2 NP - r2 P
Lotka-Volterra predator-prey:
Equilibrium predictions
• At equilibrium
• dN / dt = 0 and dP / dt =0
• there is a specific, constant density of
predators, above which prey cannot increase
• there is a specific, constant density of prey,
below which predator cannot increase
Lotka-Volterra predator-prey
isoclines
PREY ISOCLINE
PREDATOR ISOCLINE
dN / dt = 0
dP / dt = 0
dP / dt < 0
dN / dt < 0
dN / dt > 0
Prey (N)
dP / dt > 0
Prey (N)
Lotka-Volterra predator-prey isoclines
dP / dt = 0
dN / dt = 0
equilibrium
Prey (N)
Lotka-Volterra predator-prey isoclines
START HERE
Prey (N)
Density (N or P)
Lotka-Volterra predator-prey
dynamics
Time (t )
Predator-prey cycles in real data
• Hare & Lynx
• What assumptions are
built into Lotka-Volterra
predator-prey models?
Simplifying Assumptions
• Simplifying Environmental
– Constant in time
– Uniform or random in space
• Simplifying Biological
–
–
–
–
Individuals are identical & constant in time
Exponential prey growth
Prey limited only by predation
Predator growth dependent only on predation
Explanatory Assumption
• Predators and prey encounter each other at
random, like bimolecular collisions
– Frequency of encounter proportional to product of
densities
• Individual predator feeding rate increases
linearly as N increases
– No limit on increase in feeding rate
Unrealistic elements
• No limits on prey except predation
– expect real prey may be limited by food, space, etc. when
abundant
– upper limit ( K ) for prey even with no predators
• Predators do not saturate with prey
– expect real predators to hit a maximum number eaten
– expect an upper limit for predators with maximal food (KP )
Gause’s
predator-prey
experiments
Didinium
Predatory
ciliate
Didinium
Paramecium
Paramecium
Prey
Density (N or P)
Didinium - Paramecium
predator-prey experiment
Paramecium
Didinium
Time (t )
Gause’s Predator-Prey experiments
•
•
•
•
•
Predator and prey in a simple environment
No cycles (stable or otherwise)
Predator exterminates prey
Predator dies out shortly after
Inconsistent with Lotka-Volterra predator-prey
models
Gause’s Modified
Predator-Prey experiments
• Regular immigration of Paramecium
• Produces cycles of predator & prey
• Consistent with Lotka-Volterra predator-prey
models?
• No
– violates simplifying assumptions
– prey population now not soley governed by
exponential growth and predation
Huffaker’s
Predator-Prey experiments
• Mites
– predator Typhlodromus
– prey Eotetranychus
• on oranges
• With oranges evenly
spread on a tray
– no cycles
– prey extinction, then
predator extinction
Huffaker’s modified
Predator-Prey experiments
• Add barriers to dispersal
• rubber balls, vaseline
– cycles
• Confirms Lotka-Volterra
prediction?
• NO
– violates simplifying
environmental assumption
Predator-Prey models
& experiments: Conclusions
•
•
•
•
Lotka-Volterra models are largely inadequate
lab systems meeting assumptions -- no cycles
Stable oscillations when system is “fixed”
Conceptual error:
– Design experiments to meet assumptions, then test
predictions
– Don’t manipulate experiments until they confirm
theory
Improved Predator-Prey models
• Self limitation of prey and predators
• Asymptotic prey consumption by
predators
• Spatial refuges for prey
• graphical approach
– Rosezweig & MacArthur (1963)
• mathematical approach
– Williams (1980) Grover (1997)
– Gilpin & Ayala (1973) Populus 5.4