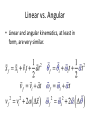Download Rotational Motion

Rotational Motion
Chapter 7
Angles
• Been working with degrees for our angles
• 90 degrees, 180, 56.4, etc.
• There is another way to measure an angle,
which is called radians
Radians
• Radians are found by the following:
Θ=(s/r)
• s is the arc length of the circle
• r is the radius of the circle
• Radians are usually some multiple of pi.
Unit circle
Radians vs. degrees
• 360 degrees is the same as 2π radians
-Degree to radian: radian = (π/180) * degree
-Radian to degree: degree = (180/π) * radian
One revolution = 2π radians = 360 degrees
Convert:
35 degrees to radians
5.6π radians to degrees
Angular displacement
• Angular displacement is how much an object
rotates around a fixed axis
• Such examples would be a tire rotating, or a
Ferris wheel car.
Angular displacement
• Finding angular displacement is simply a
matter of finding the angle in radians:
Δθ=(Δs/r)
• So the change in angular displacement is
equal to the change in arc length over the
radius.
Sample Problem
• A Ferris wheel car travels an arc length of 30
meters. If the wheel has a diameter of 45
meters, what is the car’s displacement?
Angular speed
• Angular speed is how long it takes to travel a
certain angular distance.
• Similar to linear speed, angular is found by:
ωavg= Δθ/Δt
and its units are rad/s, though rev/s are often
used as well
Sample Problem
• An RC car makes a turn of 1.68 radians in 3.4
seconds. What is its angular speed?
Angular acceleration
• Lastly, angular acceleration is how much
angular speed changes in that time interval.
αavg=(ω2-ω1)/Δt
The units are rad/s2 or rev/s2, depending on
angular velocity
Sample problem
• The tire on a ‘76 Thunderbird accelerates from
34.5 rad/s to 43 rad/s in 4.2 seconds. What is
the angular acceleration?
Episode V: Kinematics Strike Back
• Displacement, speed, acceleration…should all
sound familiar
• Recall the linear kinematics we discussed
earlier.
Linear vs. Angular
• Linear and angular kinematics, at least in
form, are very similar.
NOTE
• These kinematic equations only apply if
ACCELERATION IS CONSTANT.
• Additionally, angular kinematics only for
objects going around a FIXED AXIS.
Sample problem
• The wheel on a bicycle rotates with a constant
angular acceleration of 3.5 rad/s2. If the initial
angular speed of the wheel is 2 rad/s, what’s
the angular displacement of the wheel in 2
seconds?
Tangential & Centripetal Motion
• Almost all motion is a mixture of linear and
angular kinematics.
• Reflect on when we talked about golf swings
in terms of momentum and impulse.
Tangents
• A tangent line is a straight line that just barely
touches the circle at a given point.
Tangential Motion
• Similarly, for an instantaneous moment in
circular motion, objects have a tangential
speed.
• So for an infinitesimally small time, an object
is moving straight along a circular path.
Tangential speed
• Tangential speed depends on how far away
the object is from the fixed axis.
Tangential speed
• The further from the axis you are, the slower
you will go.
• The closer to the axis you are, the faster you
will go.
Tangential speed
• So, during a particular (infinitesimally small)
time on the circular path, the object is moving
tangent to the path.
• No circular path, no tangential speed
Tangential speed
• The tangential speed of an object is given as:
vt=rω
where r is the distance from the axis, or the
radius of a circle.
Remember, the units for linear speed is m/s.
Sample problem
If the radius of a CD in a computer is .06 m and
the disc turns at an angular speed of 31.4
rad/s, what’s the tangential speed at a given
point on the rim?
Tangential acceleration
Of course, where there is speed, there probably
is also acceleration
But keep in mind: THIS IS NOT AN AVERAGE
ACCELERATION.
INSTANTANEOUS Tangential
Acceleration
• Tangential acceleration also points tangent to
the circular path, found by:
at=rα
Sample Problem
• What is the tangential acceleration of a child
on a merry-go-round who sits 5 meters from
the center with an angular acceleration of
0.46 rad/s2?
Centripetal Acceleration
• You can make a turn at a constant speed and
still have a changing acceleration. Why?
Centripetal Acceleration
• Remember, acceleration is a VECTOR, just like
velocity.
• So when you’re pointing in a different
direction along a circular path, acceleration is
changing, even though velocity is constant.
• This is known as centripetal acceleration.
Centripetal Acceleration
• Centripetal acceleration points TOWARDS the
center of the circular path.
Centripetal acceleration
• There are two ways to determine this
acceleration:
ac=vt2/r
OR
ac=rω2
Sample problem
A race car has a constant linear speed of 20 m/s
around the track. If the distance from the car
to the center of the track is 50 m, what’s the
centripetal acceleration of the car?
Acceleration
• Centripetal and tangential acceleration are
NOT IDENTICAL.
• Tangential changes with the velocity’s
magnitude.
• Centripetal changes with the velocity’s
direction.
Total Acceleration
• Finding the total acceleration of an object
requires a little geometry.
Causes of circular motion
Circular Motion
• If you’ve ever gone round a sharp turn really
fast, you probably feel yourself being tilted to
one side.
• This is due to Newton’s Laws
Back to THOSE…
• Objects resist changes in motion.
• When you go round a curve, your body wants
to keep going in a linear path but the car does
not.
Once more…
• So for a linear path, if F=ma, then for a circular
path, Fc=mac
• This is known as centripetal force.
Centripetal Force
• There are two other ways to find this force.
Fc=(mvt2)/r
OR
Fc=mrω2
Sample problem
A 70.5 kg pilot is flying a small plane at 30 m/s in
a circular path with a radius of 100 m. Find
the centripetal force that maintains the
circular motion of the pilot.
Conundrum
• Centripetal force points towards the center of
the axis.
• BUT in a car, you feel like you’re being flung
AWAY from the center of axis.
• So, what gives?
When in doubt, Newton
• Your body’s inertia wants to keep going in a
linear direction. Which is why you tend to tilt
away from the center of axis on a curve.
• This is often labeled as centrifugal force, but it
is NOT a proper force.