Download I. Electric flux

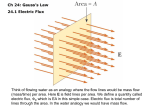
In our first two units on electrostatics we considered the electric field due to one or more point charges and
also due to a uniform charge distribution. In our final unit on electro-statics we will investigate a third way
to determine the electric field at a point in space when there is an extremely high degree of symmetry in the
charge distribution. This entire unit is concerned with a single equation, Gauss’s Law of Electricity. This
also happens to be the first of Maxwell’s set of four equations. Now we are getting somewhere, eh! Before
taking test 303 students should be familiar with all of the material in the outline below.
I. Electric flux
A. Flux and charge
B. Flux and field
II. Gauss’s Law of Electricity
A. Planar symmetry
1. Non-conducting sheet
2. Conducting sheet
B. Cylindrical symmetry
1. Line Charge
2. Conducting, concentric, cylindrical shell(s)
3. Solid cylinder(s) of charge distributions
a) Uniform charge distributions
b) Charge distributions that vary as a f(r)
C. Spherical symmetry
1. Point Charge
2. Conducting, concentric, spherical shell(s)
3. Solid spherical charge distributions
a) Uniform charge distributions
b) Charge distributions that vary as a f(r)
D. Graphing E(r) and V(r) for all r
Students who are fully prepared for test 303 will know how to apply Gauss’s Law of Electricity
to each of the situations from the previous page. Part (D) was actually covered in the last lesson
of the previous unit. You have been warned that you will see it again on this test. 
Lesson 3-14
Read Section 24:1-4
Electric Flux Defined
In our initial lesson we will consider two definitions of electric flux. Before we get to
those definitions one should read the textbook’s idea of flux. Initially, flux is related to
the flow rate of a fluid through a membrane or boundary. In this unit our boundary will
be a closed surface that will totally encapsulate a finite amount of charge. In most cases
you can picture a charge to be surrounded by an expandable or collapsible bubble, like a
soap bubble. We call this imaginary, closed surface a Gaussian Surface. See figure 24.1.
At first inspection one would think that figure 24.1 is showing a Gaussian Surface with
some lines of force sticking out through the surface. There is one major difference,
however. The lines of force are infinite and will go through every point on the Gaussian
Surface at the same time. But these lines are finite. We call them the lines of flux. This
brings us to our first revelation about flux.
The lines of flux will flow in the same direction as the lines of force; the flux lines
will be finite in contrast to the infinite number of lines of force.
We need a symbol for flux and the letter that is chosen is the Greek equivalent of “F” for
flux. We will use the symbol, E, for electric flux. Electric flux has the dimensions or
units of (N-m2/C) or (Joule-m/C) or (Kg-m3)/(s2-C).
Flux and Charge
Suppose that a student placed a charge of +q inside of a paper bag. Also suppose that
although you cannot see what is inside of the bag you find the there are N lines of flux
poking out through the surface of the bag. A second student comes along with a paper
bag and you notice that she has 4N lines of flux sticking into her bag. You could
conclude that she has a negative, net charge inside of the bag because the flux lines are
flowing into the bag instead of out of the bag. You could also conclude that her net
charge is –4q in comparison to the first student’s bag with its charge of +q. Now you
could not conclude if the second person had charge inside of the bag that was –5q and +q
or –6q and +2q or merely –4q but you could at least conclude what the net charge is
inside of her bag. This should all make sense if the following is true.
The total amount of flux sticking into or out of a Gaussian Surface is dependent
upon the net charge inside of the surface.
This brings us to our first definition of electric flux. We assume that E  qIN where we
consider only the charge inside of the Gaussian Surface. By careful measurements in a
lab we can turn the proportionality into an equation by introduction of
a constant. The proportionality constant is o = 8.85E-12 C2/(N-m2).
E = qIN/ o
Epsilon naught is known as the permittivity of free space and can be
thought of as the measurement of the maximum number of flux lines that can be emitted
by an elementary charge in a vacuum. Of course plugging in the smallest unit of charge,
that of the electron, into the above equation yields a result of less than one line per
electron. We could fix this by redefining our metric system but that is another story for
another time.
Electric Flux and Electric Field
There is also a relationship between E and E. It just so happens that E is also known as
the flux density. When the electric field strength is high the flux lines are really dense
and when the electric field strength is weak the flux lines are spread really far apart. To
put it bluntly, the electric field strength E is a measure of the flux density. Suppose that
the spherical Gaussian Surface of figure 24-1 could be expanded much like a balloon. As
the surface area increases a point on the surface would move farther away from the point
charge. Although the same amount of flux sticks out of the surface, the lines are farther
apart causing the electric field to be weaker.
This point is also made in figure 24-3 where some lines go into and out of a heartshaped surface. The heart-shaped surface has some small rectangular partitions that are
almost perpendicular to the flux while others are almost tangent to the flux. For the three
partitions that are specifically inspected in figure 24-3 notice that the area A has a
vector direction that is normal to the surface and sticking outward. This leads us to our
second definition of flux but first we must make two significant points.
1. The total amount of flux is equal to the product of (flux/area) times area.
2. The electric field components perpendicular to the surface area are the only
ones that count for total flux. In order to accomplish this the vector direction
of E and A must be parallel.
We can construct an equation that relates the electric flux and the electric field strength as
suggested in part 1 while accommodating the condition stressed
in part 2. The equation is stated in the box to the right. Study
E = E  A
Sample Problems 24-1 thru 24-3 and checkpoints 1 & 2.
In order to get a true count of all lines going into or out of a closed surface one
must allow the number of partitions to approach infinity while the size of each A
approaches zero in value. As this takes place the above-boxed equation will turn into an
integral over a closed surface. We place a circle over the integral sign to remind us that
the surface area must be a closed Gaussian Bubble or some shape like cube, sphere,
cylinder or so forth. By allowing the latter box to turn into an integral expression and
setting the two definitions of flux equal to each other we arrive at an equation known as
Gauss’s Law of Electricity. It relates the electric field
strength on the surface of the Gaussian bubble to the


q IN /  o   E  dA
charge enclosed inside of the bubble. This equation
is really quite messy unless there is a high degree of
symmetry. The rest of this unit is dedicated to the application of the above equation.
Homework Problems Ch 24: 1-11
These problems are very elementary and will only count 2 points per solution instead of
the customary 3 points.
Lesson 3-15
Read Section 24:5-8
Gauss’s Law Basics
Point q’s, line q’s & Planar q’s
For our introductory lesson of Gauss’s Law we will apply it to the basic forms of
symmetry. These are the electric field of a point charge, a uniform linear charge and a
uniform surface charge or sheet of charge on a conducting plane as well as a nonconducting plane. You should commit today’s results to memory for all boxed equations.
Gauss’s Law Basics
In most instances the purpose for using Gauss’s Law is to find the electric field
strength, E, at the surface of the Gaussian Bubble or envelope. There are a few things
that you can do to make the math simplify:
a) Select a correct shaped Gaussian surface so that E is everywhere either perpendicular
or tangent to the surface. This will make the cosine part of the dot product either zero
or one in value.
b) Select a correct shaped Gaussian surface that is centered on the charge so that E has
the same value at every point along the surface. This will allow E to become a
constant of the integration in order to be factored outside of the integral.
c) If steps (a) and (b) are accomplished then Gauss’s Law
E = qIN/(Ao)
will reduce to the algebraic form shown in the box to
the right.
The Point Charge
Figure 24-8 shows a positive point charge that is surrounded by a yellow, spherical
Gaussian bubble. Since the charge is centered on the bubble then E has the same value at
all points on the surface of the bubble. E is also perpendicular to the surface at all points
making each E vector parallel to each dA vector. The surface of a sphere is 4r2. The
following result occurs:


a) q IN /  o   E  dA
b) q/o = E(4r2) c) Solving for E  E = (1/4o)q/r2
The final result is our familiar expression for the electric field due to a point charge
except that we now recognize the constant k = 9E+9 Nm2/C2 is composed of a more
fundamental constant, o.
The Line Charge
Figure 24-12 shows a very long (assumed infinite), uniform charge that is fixed along a
vertical line. We assume that the charge per unit length is a constant value of . By
picking a cylindrical shaped Gaussian Surface we recognize that E is normal to the lateral
surface area of the cylinder and tangent to the end caps. Since flux only penetrates the
side of the cylinder and not the end caps the only area we need to consider is the side.
The surface area of the side is 2rh. The following result occurs:


a) q IN /  o   E  dA
b) q/o = E(2rh) but q/h = 
c) Solving for E  E = (/2o) 1/r
Anytime that you are outside of any cylindrical charge distribution you can treat it like a
line charge. This is why you must commit this result to memory.
Planar Charge Distributions for Conducting Surfaces
When dealing with planar charge distributions it is critical that you first recognize
whether or not the surface is conducting. It makes a difference in your final solution.
The authors go to great length in section 24-6 to stress that following points:
a) Any excess charge placed on a solid conductor will remain on the surface.
b) There is no electric field inside of a conductor under static conditions.
c) E is always perpendicular to the surface of a conductor.
d) Under static conditions E will not penetrate a conducting surface.
e) The charge per unit area, , can vary over the surface
Figure 24-10 shows a charged conducting surface with a cylindrical Gaussian bubble. In
this instance the flux penetrates one of the end caps and is now tangent to the lateral
surface area. The end cap has area A. The following result leads us to the value of the
electric field “just above the conducting surface”. This is a limiting value.


a) q IN /  o   E  dA
b) qIN/o = EA but qIN/A = 
c) Solving for E  E = /o
For planar surfaces we assume that  is a constant thus making the electric field constant.
Planar Charge Distributions for Non-Conducting Surfaces
Figure 24-15 shows an infinite sheet of charge suspended in space. Notice that the sheet
of charge in not on the surface of a conductor so that flux may leave the charged sheet
from both sides. Again, a cylinder is used for the Gaussian surface. The flux is tangent
to the lateral surface area and may be neglected in Gauss’s Law. In contrast to the last
example, here we see flux penetrating both end caps. The following result occurs as long
as you are very close to the surface of the charge and not too close to the edge of the
sheet of charge.


a) q IN /  o   E  dA b) qIN/o = E(2A) but qIN/A = 
c) Solving for E  E = /2o
You should read the section on two conducting plates on page 590 and review Sample
Problem 24-6 before attempting the homework.
Homework Problems Ch 24: 17, 19, 22, 32, 33, 35*, 37
* Include a free-body diagram and sum the forces in the x and y directions.
Lesson 3-16
Read Section 24:5,6, and 9
Gauss’s Law and
Spherical Symmetry
With spherical symmetry one must use a spherical Gaussian surface. Recall that the
surface area of a sphere is 4r2 and the volume of a sphere is 4/3 r3. We consider the
following examples employing Gauss’s Law for systems with spherical symmetry.
Example #1
An excess charge of Q is placed on a solid conducting sphere or radius “R”. Determine
the electric field strength both inside and outside of the sphere. See the discussion at the
beginning of section 24:9 including equations 24-15 and 24-16. The situation is shown in
figure 24-18. For r > R you should get the solution of a point charge of Q. For r < R the
electric field is zero since all charge resides on the surface of the conductor.
Example #2
A point charge of Q is placed at the center of a neutral, hollow conducting sphere of inner
radius “a” and outer radius “b”. Find the electric field for the regions r > b, a > r > b and
for r < a. Also, determine the charge density on the inner and outer surface of the
conducting spherical shell. Sample Problem 24-4 will give you great insight in how to
work this problem. For r > b you can treat the system as a point charge so that E = kQ/r2.
For a < r < b all points are inside of a conductor and E = 0. For r < a you can again use
the solution for a point charge, E = kQ/r2. The charge density on the inner surface of the
spherical shell is  = -Q/(4a2). The outer surface has charge density is  = +Q/(4b2).
Example #3
An excess charge of Q is distributed uniformly throughout a sphere of radius R. Give
solutions in terms of Q and also in terms of  where  = 3Q/(4R3) for the regions both
inside and outside of the sphere. Sample Problem 24-7 demonstrates this type of
problem.
Example #4
A solid sphere has a radius of R and a charge distribution that varies according to  = Cr2.


This variable charge distribution is shown in fig. 24-19.

dV


E

d
A
o

When the charge density is not uniform you have to
integrate both sides of the equation. Since the density
varies according to the radius only we can break the charge into concentric spherical
shells. Each spherical shell has a differential volume of dV = 4r2dr.
Homework Problems Ch 24: 43, 44, 45, 46, 47, 48, 52, 53, 55 (dE/dr = 0). For each
problem draw a charge distribution and clearly label the Gaussian surfaces for each
region. Feel free to make different Gaussian Surfaces different colors so that you do not
have to redraw the charge distribution over and over again.
Gauss’s Law and
Cylindrical Symmetry
Lesson 3-17
Read Section 24:7
If the charge is distributed along one dimension then the flux can only spread along two
instead of three dimensions. The consequence of this loss of one dimension causes the
electric field strength (a.k.a. flux density) to decrease by one less power. Expect to see
many 1/r functions in contrast to the 1/r2 functions of yesterday. Also, we choose a
cylindrical Gaussian surface for today’s problems. In most instances the flux penetrates
only the lateral surface area. We will work problems 24:22, 24, 26 and 28 in class.
Homework Problems Ch 24: 25, 27, 29, 30, 31. For each problem draw a charge
distribution and clearly label the Gaussian surfaces for each region. Feel free to make
different Gaussian Surfaces different colors so that you do not have to redraw the charge
distribution over and over again.
Lesson 3-18
Review
Graphing E(r) & V(r)
The most common problem on the AP Free-Response Exam is to be given a charge
distribution with which you must do the following:
a) Use Gauss’s Law of Electricity to find E(r) for each region from 0 < r < . This is
what chapter 24 is all about. The only working equation is shown below.


 dV   o  E  dA
b) Use your expressions for E(r) to determine V(r) for each region starting with V = 0 at
r = . We did this at the end of the last unit. The only working equation is shown
below:
f


V f  Vo    E  dS
o
c) Graph both E and V. When graphing you do not have to have a continuous graph for
the electric field strength, E. The discontinuities will occur where there are
conducting boundaries. The electric potential graphs, however, MUST be
continuous, smooth curves from 0 to infinity. In order to guarantee this characteristic
of the potential graph we will start at infinity and integrate inward, matching
functions at each boundary that we encounter.
We end this unit with a few examples. Expect a test real soon. We are now through with
electrostatics! There are only four units remaining in the year before we start to review
for the exam.