Download Quiz 4

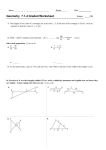
Math 99
Quiz 4
10/22/07
Name: __________________________
+_____
60
Write your name bigger on the back. If you need scratch paper, please ask me. For full credit, show
all work as discussed in class. Use algebra to solve the following problems.
1. Suppose that a system has infinitely many ordered triple solutions of the form (x,y,z) such that
x  y  2 z  1 . Give three specific ordered triples that are solutions of the system. Why do they
work?
x=__________________________
y=__________________________
z=__________________________
_____
3 pts
2. Add –2 times Equation 1 to Equation 2. What effect does this operation have?
x  3y  4z  4

2 x  5 y  3z  1

3 y  4 z  5

Resulting equation: __________________________
Effect: __________________________
_____
3 pts
3. Solve the following systems of equations. If the system has infinitely many solutions, then state
the plane on which the solutions lie. Otherwise, state the single coordinate that is the solution or
write no solution. Be sure to show work clearly for full credit.
a.
3x  5 y  z  6

x  y  3 z  1

2x  2 y  6z  5

b.
2 x  5 y  7 z  10

 6 x  15 y  21z  30

4 x  10 y  14 z  20

c.
4x  3y  2z  5
5 y  z  11
3 z  12


_____
6 pts

_____
6 pts
_____
6 pts
Solution:
____________________
Solution:
____________________
Solution:
____________________
/ 24 pts total
4. Which values should be given to a, b, and c so that the linear system has (-1,2,-3) as its only
solution?
x  2 y  3z  a
x yz b
2x  3y  2z  c
a=__________________________
_____
6 pts
b=__________________________
c=__________________________
5. To make a 10% acid solution for chemistry class, Xavier wants to mix some 5% solution with
10 L of 20% solution. How many liters of 5% solution should he use? (Hint: Draw a picture.)
_____
7 pts
Define variables: ________________________________________________________
System of equations:
Work:
Solution:__________________________
6. The two top-grossing movies of 2001 were Harry Potter and the Sorcerer’s Stone and Shrek.
Shrek grossed $26 million less than Harry Potter and the Sorcerer’s Stone, and together, the
two films took in $562 million. (Source: ACNielsen EDI)
_____
5 pts
a. How much did each of these movies earn?
Define variables: ________________________________________________________
System of equations:
Work:
Solution:__________________________
/ 18 pts total
b. If Shrek earned $27 million more than Monsters, Inc., how much did Monsters, Inc.
earn?
_____
2 pts
__________________________
c. What is the total amount these top three films earned?
_____
2 pts
__________________________
For problems 7 and 8, setup the system for the following story problems, but do not solve.
7. The sum of three numbers is 189. The first number is 28 less than the second number. The
second number is 21 less than the sum of the first and third numbers. Find the three numbers.
_____
7 pts
Define variables: ________________________________________________________
System of equations:
8. On a trip from Chicago to Seattle, an airplane flying against the wind took three and one-half
hours to make the 1827 mile trip. That same day, the return trip by the plane flying with the
same wind, took three hours. Find the speed of the plane and the speed of the wind that day.
_____
7 pts
Define variables: ________________________________________________________
Distance
Rate
Time
With wind
Against wind
System of equations:
Extra Credit (4 extra points possible)
Only work on this problem if you have time left over. Do the work on a separate page. Be sure to
define variables, show your system of equations, and work in solving the system.
 A wallet contains $218 in $10, $5, and $1 bills. There are 46 bills in all, and four more
$5 bills than there are $10 bills. How many bills of each kind are there?
/ 18 pts total