Handout - UNT Chemistry
... Note: We cannot actually derive Quantum Mechanics or the Schrödinger Equation. In the last slide, we gave a rationalization of how, if a particle behaves like a wave and is given by the de Broglie relation, then the wavefunction, , satisfies the wave equation proposed by Erwin Schrödinger. Quant ...
... Note: We cannot actually derive Quantum Mechanics or the Schrödinger Equation. In the last slide, we gave a rationalization of how, if a particle behaves like a wave and is given by the de Broglie relation, then the wavefunction, , satisfies the wave equation proposed by Erwin Schrödinger. Quant ...
Part 2: Quantum theory of light
... underlying fact that Nature does not allow a particle to possess definite values of position and momentum at the same time. This principle (which would be better described by the term "indeterminacy" than "uncertainty") has been thoroughly verified and has far-reaching practical consequences which ...
... underlying fact that Nature does not allow a particle to possess definite values of position and momentum at the same time. This principle (which would be better described by the term "indeterminacy" than "uncertainty") has been thoroughly verified and has far-reaching practical consequences which ...
Development of the Atomic Model
... Albert Einstein • Einstein expanded on Planck’s theory by introducing wave-particle duality of light. • That is, while light has many wave like characteristics, it can also be thought of as a stream of particles or bundles of energy. (each of which carries a quantum of energy). • Einstein called th ...
... Albert Einstein • Einstein expanded on Planck’s theory by introducing wave-particle duality of light. • That is, while light has many wave like characteristics, it can also be thought of as a stream of particles or bundles of energy. (each of which carries a quantum of energy). • Einstein called th ...
Lecture 9
... PHYSICS 244 NOTES Lecture 9 Comparing with experiment Introduction In classical mechanics, with the motion of a particle described by its trajectory function r(t), comparing theory and experiment is pretty straightforward. We set our watch and our coordinate system. At time t we look for the particl ...
... PHYSICS 244 NOTES Lecture 9 Comparing with experiment Introduction In classical mechanics, with the motion of a particle described by its trajectory function r(t), comparing theory and experiment is pretty straightforward. We set our watch and our coordinate system. At time t we look for the particl ...
ARRANGEMENT OF ELECTRONS IN ATOMS
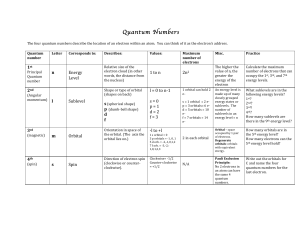
... - ______________________________ () - the distance between corresponding points on adjacent waves - meter, centimeter, or nanometer (1 nm = 1 x 10 -9 m) is unit for measuring - ________________________________ ( v ) - the number of waves that pass a given point in a specific time, usually one secon ...
... - ______________________________ () - the distance between corresponding points on adjacent waves - meter, centimeter, or nanometer (1 nm = 1 x 10 -9 m) is unit for measuring - ________________________________ ( v ) - the number of waves that pass a given point in a specific time, usually one secon ...
ATOMIC PHYSICS REVISION NOTES:
... For example, the outer shell of Bi has three electrons with n = 6 and l = 1 - the rst two have j = 1=2 and since this is then full, the third must have j = 3=2, This outer sub-shell is denoted by (6p)212 (6p) 32 Below this sub-shell Bi has a closed sub-shell with n = 4; 3, which has a total of 14 e ...
... For example, the outer shell of Bi has three electrons with n = 6 and l = 1 - the rst two have j = 1=2 and since this is then full, the third must have j = 3=2, This outer sub-shell is denoted by (6p)212 (6p) 32 Below this sub-shell Bi has a closed sub-shell with n = 4; 3, which has a total of 14 e ...
Atomic questions
... In the Geiger-Marsden experiment, α particles are scattered by gold nuclei. The experimental results indicate that most α particles are A. ...
... In the Geiger-Marsden experiment, α particles are scattered by gold nuclei. The experimental results indicate that most α particles are A. ...
Quantum Mechanics and Spectroscopy for Mechanical Engineers
... Classical mechanics, which is used to model the dynamics of macroscopic objects, is a limiting case of the more general theory of quantum mechanics. At present, quantum mechanics provides the most complete description of the behavior of a physical system. At the core of quantum mechanics is the De B ...
... Classical mechanics, which is used to model the dynamics of macroscopic objects, is a limiting case of the more general theory of quantum mechanics. At present, quantum mechanics provides the most complete description of the behavior of a physical system. At the core of quantum mechanics is the De B ...
Document
... For constant intensity, the # of electrons decreases with increasing frequency If the frequency is below a certain level, no electrons are ejected, regardless of intensity ...
... For constant intensity, the # of electrons decreases with increasing frequency If the frequency is below a certain level, no electrons are ejected, regardless of intensity ...