1. Calculate the partition function of the hydrogen atom at room
... where p = 2mE ≡ k and p′ = 2m(E − V0 ) ≡ k ′ are the momenta of the particle to the left and to the right of the barrier (and k and k’ are the corresponding wavevectors). Notice that Planck’s constant does not enter the above expression at all. Since quantum mechanics is a better theory than class ...
... where p = 2mE ≡ k and p′ = 2m(E − V0 ) ≡ k ′ are the momenta of the particle to the left and to the right of the barrier (and k and k’ are the corresponding wavevectors). Notice that Planck’s constant does not enter the above expression at all. Since quantum mechanics is a better theory than class ...
The Method of Moment Generating Functions
... exists there exists a positive number b such that mY (t) is finite for all t such that |t| ≤ b. Proposition 4.2. ...
... exists there exists a positive number b such that mY (t) is finite for all t such that |t| ≤ b. Proposition 4.2. ...
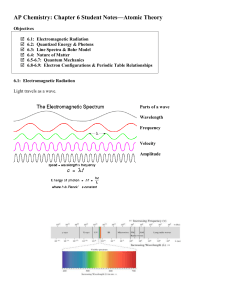
Ch. 6 notes
... 6.5-6.7: Quantum Mechanics Developed by Werner Heisenberg (1901-1976), Louis De Broglie (1892-1987), Erwin Schrodinger (1887-1961) This answers the question: Where is the _____________ in the atom? The answer is complex. We can’t say exactly where the atom is. We can only say where we think it _____ ...
... 6.5-6.7: Quantum Mechanics Developed by Werner Heisenberg (1901-1976), Louis De Broglie (1892-1987), Erwin Schrodinger (1887-1961) This answers the question: Where is the _____________ in the atom? The answer is complex. We can’t say exactly where the atom is. We can only say where we think it _____ ...
SOME STRANGE FEATURES OF THE GALILEI GROUP BARBARA GOŁUBOWSKA, VASYL
... The peculiarity of Minkowski-Poincare structure is the existence of some fixed universal physical constant-velocity of light c. In a sense the traditional Galilei structure is obtained in the limit transition c → ∞. And in fact there are numerous formulae in which this limit is smoothly achieved. Bu ...
... The peculiarity of Minkowski-Poincare structure is the existence of some fixed universal physical constant-velocity of light c. In a sense the traditional Galilei structure is obtained in the limit transition c → ∞. And in fact there are numerous formulae in which this limit is smoothly achieved. Bu ...
Quantum Theory 1 - Home Exercise 4
... 4. Particle on a ring - Consider a particle that is free to move on a ring of circumference L, such that ψ(x, t) = ψ(x + L, t) (a) Find the normalized stationary states of the system and explicitly show that they form an orthonormal basis. (b) Calculate the dispersion relation ωn (kn ) and show that ...
... 4. Particle on a ring - Consider a particle that is free to move on a ring of circumference L, such that ψ(x, t) = ψ(x + L, t) (a) Find the normalized stationary states of the system and explicitly show that they form an orthonormal basis. (b) Calculate the dispersion relation ωn (kn ) and show that ...
Particle on a Sphere
... Designated by letters: s, p, d, f, … Specifies the shape of an orbital Magnetic quantum number = ml Determines the z component of orbital angular momentum Z component = ml restricted to values: Specifies orientation of orbital in space ...
... Designated by letters: s, p, d, f, … Specifies the shape of an orbital Magnetic quantum number = ml Determines the z component of orbital angular momentum Z component = ml restricted to values: Specifies orientation of orbital in space ...
Please look over the following review questions
... corresponds to all theories in nature updates the essence of the old theory ties two or more theories together accounts for verified results of the old theory none of these ...
... corresponds to all theories in nature updates the essence of the old theory ties two or more theories together accounts for verified results of the old theory none of these ...
Quantum Mechanics
... Quantum fields fill all space; one field for each kind of particle. Particles are just localized bunches of energy carried by the fields. Particles can appear and disappear spontaneously from the fields. Perhaps the universe appeared in just this way. ...
... Quantum fields fill all space; one field for each kind of particle. Particles are just localized bunches of energy carried by the fields. Particles can appear and disappear spontaneously from the fields. Perhaps the universe appeared in just this way. ...
Slide 1
... In zero field there is a low-energy doublet, which we call This is separated from a 3rd state ...
... In zero field there is a low-energy doublet, which we call This is separated from a 3rd state ...
ppt - HEP Educational Outreach
... – Aims to describe the most fundamental objects in nature and the force laws that govern their interactions. – Currently: Standard Model (SM) • 6 Quarks, 6 leptons, and force carriers (g, gluon, W±, Z) • Works very well, but certainly an effective theory ...
... – Aims to describe the most fundamental objects in nature and the force laws that govern their interactions. – Currently: Standard Model (SM) • 6 Quarks, 6 leptons, and force carriers (g, gluon, W±, Z) • Works very well, but certainly an effective theory ...
2 Properties of 3jm- and 3nj-Symbols
... 2.1 Properties of 3jm-Symbols Basic elements in the theory of angular momentum are the Clebsch–Gordan coefficients for coupling two states characterized by j1 , m1 and j2 , m2 into a new state with quantum numbers J, M . The numbers j and their projections, or magnetic quantum numbers1 , m have intege ...
... 2.1 Properties of 3jm-Symbols Basic elements in the theory of angular momentum are the Clebsch–Gordan coefficients for coupling two states characterized by j1 , m1 and j2 , m2 into a new state with quantum numbers J, M . The numbers j and their projections, or magnetic quantum numbers1 , m have intege ...
Heisenberg`s Uncertainty Principle
... It is an absolute article of faith of modern physics that the uncertainty principle can be restated in terms of energy and time ...
... It is an absolute article of faith of modern physics that the uncertainty principle can be restated in terms of energy and time ...
Dr.Eman Zakaria Hegazy Quantum Mechanics and Statistical
... The value of Z that minimize E can be interpreted as an effective charge. That fact that Z comes out to be less than 2 reflects the fact that each electron partially screens the nucleus from the other , so that net effective nuclear charge is reduced from 2 to 27/16 (1.68). ...
... The value of Z that minimize E can be interpreted as an effective charge. That fact that Z comes out to be less than 2 reflects the fact that each electron partially screens the nucleus from the other , so that net effective nuclear charge is reduced from 2 to 27/16 (1.68). ...
Appendix
... After this we can, for our purposes, forget further quantum effects and treat the later evolution of the inflaton field, both the background and the perturbation, classically. The effect of the vacuum fluctuations was to produce “out of nothing” the perturbations δϕk . We can’t predict their individ ...
... After this we can, for our purposes, forget further quantum effects and treat the later evolution of the inflaton field, both the background and the perturbation, classically. The effect of the vacuum fluctuations was to produce “out of nothing” the perturbations δϕk . We can’t predict their individ ...
Renormalization group

In theoretical physics, the renormalization group (RG) refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales. In particle physics, it reflects the changes in the underlying force laws (codified in a quantum field theory) as the energy scale at which physical processes occur varies, energy/momentum and resolution distance scales being effectively conjugate under the uncertainty principle (cf. Compton wavelength).A change in scale is called a ""scale transformation"". The renormalization group is intimately related to ""scale invariance"" and ""conformal invariance"", symmetries in which a system appears the same at all scales (so-called self-similarity). (However, note that scale transformations are included in conformal transformations, in general: the latter including additional symmetry generators associated with special conformal transformations.)As the scale varies, it is as if one is changing the magnifying power of a notional microscope viewing the system. In so-called renormalizable theories, the system at one scale will generally be seen to consist of self-similar copies of itself when viewed at a smaller scale, with different parameters describing the components of the system. The components, or fundamental variables, may relate to atoms, elementary particles, atomic spins, etc. The parameters of the theory typically describe the interactions of the components. These may be variable ""couplings"" which measure the strength of various forces, or mass parameters themselves. The components themselves may appear to be composed of more of the self-same components as one goes to shorter distances.For example, in quantum electrodynamics (QED), an electron appears to be composed of electrons, positrons (anti-electrons) and photons, as one views it at higher resolution, at very short distances. The electron at such short distances has a slightly different electric charge than does the ""dressed electron"" seen at large distances, and this change, or ""running,"" in the value of the electric charge is determined by the renormalization group equation.