$doc.title
... e.g. the set of sin(nkx) & cos(nkx) functions of the’ waves in a box’ - cf Fourier components Any other function can be expressed as a linear combination of these functions ...
... e.g. the set of sin(nkx) & cos(nkx) functions of the’ waves in a box’ - cf Fourier components Any other function can be expressed as a linear combination of these functions ...
NonequilibriumDynamicsofQuarkGluonPlasma
... State of matter in which quarks and gluons are unconfined. Manifest of asymptotic freedom in Quantum Chromodynamics (QCD) Characteristic phase transition at 10 5 10 6 s in the cosmological standard model. Different models of heavy ion collisions are studied at RHIC/Brookhaven and LHV/CERN. Lifet ...
... State of matter in which quarks and gluons are unconfined. Manifest of asymptotic freedom in Quantum Chromodynamics (QCD) Characteristic phase transition at 10 5 10 6 s in the cosmological standard model. Different models of heavy ion collisions are studied at RHIC/Brookhaven and LHV/CERN. Lifet ...
PHY 551 - Stony Brook University
... Coupling constant: numerical coefficient that occur as a parameter whenever there’s an interaction. Strength of interaction ~ magnitude of a coupling constant ...
... Coupling constant: numerical coefficient that occur as a parameter whenever there’s an interaction. Strength of interaction ~ magnitude of a coupling constant ...
GCOE13_5
... Higgs field as inflaton (4) Because the logarithmical change of λ in the first term is slow compared to the power behavior of the second term, the saddle point arises near the left zero of λ(Λ) , and we can approximate it as c ...
... Higgs field as inflaton (4) Because the logarithmical change of λ in the first term is slow compared to the power behavior of the second term, the saddle point arises near the left zero of λ(Λ) , and we can approximate it as c ...
PowerPoint
... the gauge theory is strongly coupled we don’t know these mixed equations… they turn out to be the EoM of strings in AdS! ...
... the gauge theory is strongly coupled we don’t know these mixed equations… they turn out to be the EoM of strings in AdS! ...
How Atoms Work - Distribution Access
... how the universe works based on the study of observable objects in motion. quantum mechanics — The science based on the study of sub-atomic particles, based on the theory that energy is absorbed or radiated in packets called quanta. wavelength — Measurement of the distance between two consecutive hi ...
... how the universe works based on the study of observable objects in motion. quantum mechanics — The science based on the study of sub-atomic particles, based on the theory that energy is absorbed or radiated in packets called quanta. wavelength — Measurement of the distance between two consecutive hi ...
Spring 2007 Colloquium Series Physics Department University of Oregon 4:00pm Thursdays, 100 Willamette
... driving force behind many scientific and technological breakthroughs over the past century, including the invention of the laser and the realization of ultracold atoms. Creating and preserving optical phase coherence are one of the two major ingredients (the other being the control of matter) for th ...
... driving force behind many scientific and technological breakthroughs over the past century, including the invention of the laser and the realization of ultracold atoms. Creating and preserving optical phase coherence are one of the two major ingredients (the other being the control of matter) for th ...
Solutions to Homework 4
... if f is continuous at (x0 , y0 )? What can you conclude if f is not continuous at (x0 , y0 )? Explain your reasoning. Solution: If f is continuous at (x0 , y0 ), the f (x0 , y0 ) = 3. If f is not continuous at this point, then either the limit of f (x, y) as (x, y) approaches (x0 , y0 ) does not exi ...
... if f is continuous at (x0 , y0 )? What can you conclude if f is not continuous at (x0 , y0 )? Explain your reasoning. Solution: If f is continuous at (x0 , y0 ), the f (x0 , y0 ) = 3. If f is not continuous at this point, then either the limit of f (x, y) as (x, y) approaches (x0 , y0 ) does not exi ...
Slides - Indico
... Without gravity one could have said that the problem is not so severe: After all, the theory must have a scale and it happens to be around 100GeV. But with gravity there is a very little flexibility. In Einstein’s gravity MP is the scale where gravitational interactions of elementary particles beco ...
... Without gravity one could have said that the problem is not so severe: After all, the theory must have a scale and it happens to be around 100GeV. But with gravity there is a very little flexibility. In Einstein’s gravity MP is the scale where gravitational interactions of elementary particles beco ...
Qualifying Exam for Graduate Students – Fall 2008
... bar. The top and bottom surfaces are both held at 100° and the two sides are held at 0°. The bar is long enough that there is no variation in the z direction (perpendicular to the page.) The steady-state temperature as a function of x and y obeys Laplace’s equation, 2T 0 . Find the steady-state ...
... bar. The top and bottom surfaces are both held at 100° and the two sides are held at 0°. The bar is long enough that there is no variation in the z direction (perpendicular to the page.) The steady-state temperature as a function of x and y obeys Laplace’s equation, 2T 0 . Find the steady-state ...
Problem Set 8 8.1 Chemical Equilibrium 8.2 Partial Pressure 8.3
... (a) Calculate the “canonical partition function” Zn (T ) for a harmonic oscillator with n oscillation quanta. (b) Calculate the “grand canonical partition function” Ξ(T, µ), where µ is the “chemical potential” for the oscillation quanta. [You’ll fix the value of µ in part (d) below.] (c) Use your an ...
... (a) Calculate the “canonical partition function” Zn (T ) for a harmonic oscillator with n oscillation quanta. (b) Calculate the “grand canonical partition function” Ξ(T, µ), where µ is the “chemical potential” for the oscillation quanta. [You’ll fix the value of µ in part (d) below.] (c) Use your an ...
Classical Mechanics and Minimal Action
... The Lagrangian of a physical system is defined to be the difference between kinetic- and potential energy. That is, if T is the kinetic energy and V the potential energy, then L = T − V. The principle that S is minimal for the path of any classical system, conveniently dubbed the principle of least ...
... The Lagrangian of a physical system is defined to be the difference between kinetic- and potential energy. That is, if T is the kinetic energy and V the potential energy, then L = T − V. The principle that S is minimal for the path of any classical system, conveniently dubbed the principle of least ...
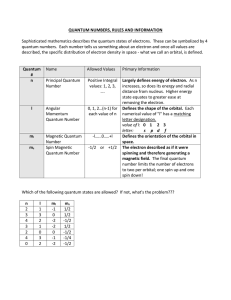
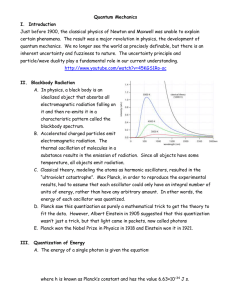
Quantum Mechanics I. Introduction Just before 1900, the classical
... results, had to assume that each oscillator could only have an integral number of units of energy, rather than have any arbitrary amount. In other words, the energy of each oscillator was quantized. D. Planck saw this quantization as purely a mathematical trick to get the theory to fit the data. How ...
... results, had to assume that each oscillator could only have an integral number of units of energy, rather than have any arbitrary amount. In other words, the energy of each oscillator was quantized. D. Planck saw this quantization as purely a mathematical trick to get the theory to fit the data. How ...
Renormalization group

In theoretical physics, the renormalization group (RG) refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales. In particle physics, it reflects the changes in the underlying force laws (codified in a quantum field theory) as the energy scale at which physical processes occur varies, energy/momentum and resolution distance scales being effectively conjugate under the uncertainty principle (cf. Compton wavelength).A change in scale is called a ""scale transformation"". The renormalization group is intimately related to ""scale invariance"" and ""conformal invariance"", symmetries in which a system appears the same at all scales (so-called self-similarity). (However, note that scale transformations are included in conformal transformations, in general: the latter including additional symmetry generators associated with special conformal transformations.)As the scale varies, it is as if one is changing the magnifying power of a notional microscope viewing the system. In so-called renormalizable theories, the system at one scale will generally be seen to consist of self-similar copies of itself when viewed at a smaller scale, with different parameters describing the components of the system. The components, or fundamental variables, may relate to atoms, elementary particles, atomic spins, etc. The parameters of the theory typically describe the interactions of the components. These may be variable ""couplings"" which measure the strength of various forces, or mass parameters themselves. The components themselves may appear to be composed of more of the self-same components as one goes to shorter distances.For example, in quantum electrodynamics (QED), an electron appears to be composed of electrons, positrons (anti-electrons) and photons, as one views it at higher resolution, at very short distances. The electron at such short distances has a slightly different electric charge than does the ""dressed electron"" seen at large distances, and this change, or ""running,"" in the value of the electric charge is determined by the renormalization group equation.