Lecture 19: Quantization of the simple harmonic oscillator Phy851 Fall 2009
... • If there is a state between 5/2 and 3/2, then a state must exist between 3/2 and 1/2 and then a state must exist below 1/2, etc… • So no states between the half integers! ...
... • If there is a state between 5/2 and 3/2, then a state must exist between 3/2 and 1/2 and then a state must exist below 1/2, etc… • So no states between the half integers! ...
Course Outline
... To enable the students understand the laws that govern the structure and properties of the atom, molecules and the nucleus. Also to provide an introduction to the elementary particles. ...
... To enable the students understand the laws that govern the structure and properties of the atom, molecules and the nucleus. Also to provide an introduction to the elementary particles. ...
Chapter 5 Physics 205 Solution of Home Work Problems
... (Figure 5.23). For the case of E < U , obtain solutions to the Shrodinger equation inside the well (0 ≤ x ≤ L) and in the region beyond (x > L) that satisfy the appropriate boundary conditions at x = 0 and x = ∞. Enforce the proper matching conditions at x = L to find an equation for the allowed ene ...
... (Figure 5.23). For the case of E < U , obtain solutions to the Shrodinger equation inside the well (0 ≤ x ≤ L) and in the region beyond (x > L) that satisfy the appropriate boundary conditions at x = 0 and x = ∞. Enforce the proper matching conditions at x = L to find an equation for the allowed ene ...
PHYS-2100 Introduction to Methods of Theoretical Physics Fall 1998 1) a)
... Homework Assignment Due Tuesday, Nov.17 1) These questions have to do with the finite square well which we worked with in class today. h2π2 a) Show that if U < ------------2- then there is exactly one energy eigenvalue, i.e. only one bound 8ma state solution, and that it has even parity. h2π2 b) Sup ...
... Homework Assignment Due Tuesday, Nov.17 1) These questions have to do with the finite square well which we worked with in class today. h2π2 a) Show that if U < ------------2- then there is exactly one energy eigenvalue, i.e. only one bound 8ma state solution, and that it has even parity. h2π2 b) Sup ...
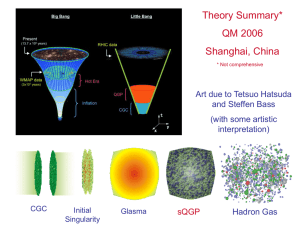
Rapporteur 4: Theory summary (30) Larry McLerran
... String Theory: About 10% off for energy density (scaled by number of degrees of freedom) But……… ...
... String Theory: About 10% off for energy density (scaled by number of degrees of freedom) But……… ...
Adventures with Superstrings
... all particle types are the same kind of string vibrating or rotating in different ways the spectrum and size of the string states is ...
... all particle types are the same kind of string vibrating or rotating in different ways the spectrum and size of the string states is ...
Homework 3
... 1. Explain the terms wavelength and amplitude. If a photon has a frequency of 9 1010 Hz what is its wavelength? Which region of the electromagnetic spectrum does this correspond to? ...
... 1. Explain the terms wavelength and amplitude. If a photon has a frequency of 9 1010 Hz what is its wavelength? Which region of the electromagnetic spectrum does this correspond to? ...
7.2 Similar Polygons - Cardinal O'Hara High School
... A. What are the pairs of congruent angles? B. What is the extended proportion for the ratios of corresponding sides? ...
... A. What are the pairs of congruent angles? B. What is the extended proportion for the ratios of corresponding sides? ...
Quantum Mechanical Model of the Atom
... • much more complicated in their shape. • so much so that we are not going to worry about them in this course!!!!! ...
... • much more complicated in their shape. • so much so that we are not going to worry about them in this course!!!!! ...
Quantum Mechanics - Indico
... At the Planck scale, Quantum Mechanics is not wrong, but its interpretation may have to be revised, not for philosophical reasons, but to enable us to construct more concise theories, recovering e.g. locality (which appears to have been lost in string theory). The “random numbers”, inherent in the u ...
... At the Planck scale, Quantum Mechanics is not wrong, but its interpretation may have to be revised, not for philosophical reasons, but to enable us to construct more concise theories, recovering e.g. locality (which appears to have been lost in string theory). The “random numbers”, inherent in the u ...
Lecture 4
... (elliptical orbits of different eccentricity) l = 0, 1, .……(n-1) ml, magnetic quantum number (describes the orientation of l in B and gives the magnitudes of the aligned components of l ) - l < ml < +l s, spin quantum number (electron spin) s = ±½ ...
... (elliptical orbits of different eccentricity) l = 0, 1, .……(n-1) ml, magnetic quantum number (describes the orientation of l in B and gives the magnitudes of the aligned components of l ) - l < ml < +l s, spin quantum number (electron spin) s = ±½ ...
Energy_and_Momentum_Units_in_Particle_Physics
... In ordinary Newtonian physics, given the kinetic energy Ek of a particle (4 Joules, say) and its momentum p (4 kg m/s), one can calculate m = p2/2Ek = 2 kg ...
... In ordinary Newtonian physics, given the kinetic energy Ek of a particle (4 Joules, say) and its momentum p (4 kg m/s), one can calculate m = p2/2Ek = 2 kg ...
Renormalization group

In theoretical physics, the renormalization group (RG) refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales. In particle physics, it reflects the changes in the underlying force laws (codified in a quantum field theory) as the energy scale at which physical processes occur varies, energy/momentum and resolution distance scales being effectively conjugate under the uncertainty principle (cf. Compton wavelength).A change in scale is called a ""scale transformation"". The renormalization group is intimately related to ""scale invariance"" and ""conformal invariance"", symmetries in which a system appears the same at all scales (so-called self-similarity). (However, note that scale transformations are included in conformal transformations, in general: the latter including additional symmetry generators associated with special conformal transformations.)As the scale varies, it is as if one is changing the magnifying power of a notional microscope viewing the system. In so-called renormalizable theories, the system at one scale will generally be seen to consist of self-similar copies of itself when viewed at a smaller scale, with different parameters describing the components of the system. The components, or fundamental variables, may relate to atoms, elementary particles, atomic spins, etc. The parameters of the theory typically describe the interactions of the components. These may be variable ""couplings"" which measure the strength of various forces, or mass parameters themselves. The components themselves may appear to be composed of more of the self-same components as one goes to shorter distances.For example, in quantum electrodynamics (QED), an electron appears to be composed of electrons, positrons (anti-electrons) and photons, as one views it at higher resolution, at very short distances. The electron at such short distances has a slightly different electric charge than does the ""dressed electron"" seen at large distances, and this change, or ""running,"" in the value of the electric charge is determined by the renormalization group equation.