String theory and the origin of the universe—new idea, old problem
... and the origin of matter and energy. Big bang theorists can attempt to describe the early universe, but so far they have not explained why there is a universe to describe. However, there have been numerous attempts at such an explanation, and recently Paul J. Steinhardt has suggested yet another ide ...
... and the origin of matter and energy. Big bang theorists can attempt to describe the early universe, but so far they have not explained why there is a universe to describe. However, there have been numerous attempts at such an explanation, and recently Paul J. Steinhardt has suggested yet another ide ...
M ph nd nd ph
... Relate the coefficients a,b,c to the parameters of the microscopic BCS Hamiltonian. Show that the coefficient a of the quadratic term changes sign at the BCS transition point, while b and c are positive. 4. Path integral for spin 1 / 2 (optional) In this problem we first introduce a fermionic repres ...
... Relate the coefficients a,b,c to the parameters of the microscopic BCS Hamiltonian. Show that the coefficient a of the quadratic term changes sign at the BCS transition point, while b and c are positive. 4. Path integral for spin 1 / 2 (optional) In this problem we first introduce a fermionic repres ...
BasicQuantumMechanics18And20January2017
... • It is impossible to simultaneously describe with absolute accuracy the energy of a particle and the instant of time the particle has this energy ...
... • It is impossible to simultaneously describe with absolute accuracy the energy of a particle and the instant of time the particle has this energy ...
Quantum Theory and Electrons as Waves
... If light could have particle-like behavior, then could matter have wave-like behavior? ...
... If light could have particle-like behavior, then could matter have wave-like behavior? ...
The Zeeman Effect
... The same expressions, but with ml and ms replaced by ML and MS, apply to the combined magnetic moments of several coupled electrons. When an atom has L≠0 and S≠0, these net magnetic moments are simply additive. Spin-orbit coupling (itself a magnetic effect) is usually large enough that the total ele ...
... The same expressions, but with ml and ms replaced by ML and MS, apply to the combined magnetic moments of several coupled electrons. When an atom has L≠0 and S≠0, these net magnetic moments are simply additive. Spin-orbit coupling (itself a magnetic effect) is usually large enough that the total ele ...
Sample Exam 3
... this electron in eV? (b) What is the orbital velocity of this electron? (Hint: You will need to figure out the kinetic energy first from the above equation.) (c) What is the principle quantum number of this orbit (remember that this number must be an integer)? (See the Constants Sheet for useful inf ...
... this electron in eV? (b) What is the orbital velocity of this electron? (Hint: You will need to figure out the kinetic energy first from the above equation.) (c) What is the principle quantum number of this orbit (remember that this number must be an integer)? (See the Constants Sheet for useful inf ...
Mid Semester paper
... (b) A particle of mass m moves under a force F (x) = −cx3 , where c is a positive constant. Find the potential energy function. If the particle starts from rest at x = −a, what is the velocity when it reaches x = 0? Where with subsequent motion does it come to rest? 8. (a) Show that for an isolated ...
... (b) A particle of mass m moves under a force F (x) = −cx3 , where c is a positive constant. Find the potential energy function. If the particle starts from rest at x = −a, what is the velocity when it reaches x = 0? Where with subsequent motion does it come to rest? 8. (a) Show that for an isolated ...
F = mv r
... Positive nucleus w/ electron orbiting about in a circle (m will refer to electron mass unless noted) Classical physics says that the electron will radiate (lose energy) and fall into the nucleus, but it doesn't. Why this is so is answered by "old" quantum theory. Bohr put forward four postulates of ...
... Positive nucleus w/ electron orbiting about in a circle (m will refer to electron mass unless noted) Classical physics says that the electron will radiate (lose energy) and fall into the nucleus, but it doesn't. Why this is so is answered by "old" quantum theory. Bohr put forward four postulates of ...
Document
... weight two. The two simplest such terms that can be written, which are lowest order in derivatives, ...
... weight two. The two simplest such terms that can be written, which are lowest order in derivatives, ...
next article
... certain particular values or "Eigenwerte." Wentzel3 and Brillouin4 have shown that in multiply periodic systems in which the variables can be separated in (4) the constants in S should as a first approximation be so chosen that the Sommerfeld phase integrals taken over a cycle are integral multiples ...
... certain particular values or "Eigenwerte." Wentzel3 and Brillouin4 have shown that in multiply periodic systems in which the variables can be separated in (4) the constants in S should as a first approximation be so chosen that the Sommerfeld phase integrals taken over a cycle are integral multiples ...
Quantum Mathematics
... information (think of kinks, instantons, phase transition, etc.), so one would expect situations in which Zi, f > 0 even in the absence of a formal proof, in system X, of statement f, from the axioms i. ...
... information (think of kinks, instantons, phase transition, etc.), so one would expect situations in which Zi, f > 0 even in the absence of a formal proof, in system X, of statement f, from the axioms i. ...
AP Physics 2 Syllabus Student
... AP Physics 2 is a one year, algebra-based course in general physics that is comparable in scope and level to the second semester of a college physics course. The course follows the College Board AP Physics 2 curriculum and prepares students to take the AP Physics 2 exam. The content in the course is ...
... AP Physics 2 is a one year, algebra-based course in general physics that is comparable in scope and level to the second semester of a college physics course. The course follows the College Board AP Physics 2 curriculum and prepares students to take the AP Physics 2 exam. The content in the course is ...
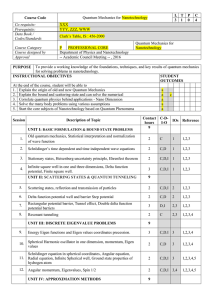
0012_hsm11gmtr_0702.indd
... 12. A scale drawing of a building was made using the scale 15 cm = 120 ft. If the scale ...
... 12. A scale drawing of a building was made using the scale 15 cm = 120 ft. If the scale ...
CLASSICAL-QUANTUM CORRESPONDENCE AND WAVE PACKET SOLUTIONS OF THE DIRAC
... well-known relation E = ~ω in the specific form H = ~W , where H is the classical Hamiltonian of a particle and W is the dispersion relation of the sought-for wave equation. We derive the expression of H in a curved space-time with an electromagnetic field. Then we derive the Dirac equation from fac ...
... well-known relation E = ~ω in the specific form H = ~W , where H is the classical Hamiltonian of a particle and W is the dispersion relation of the sought-for wave equation. We derive the expression of H in a curved space-time with an electromagnetic field. Then we derive the Dirac equation from fac ...
Quantum Mechanical Model of the Atom and Electronic Structure 1
... When electrons one, energy is This change in of the emitted ...
... When electrons one, energy is This change in of the emitted ...
Module code SP-2301 Module Title Concepts in Modern Physics
... On successful completion of this module, a student will be expected to be able to: Lower order : 30% - understand the basic principles related to modern physics, which includes relativity, matter waves, energy quantisation, x-ray and also laser generation, and the nuclear structure Middle orde ...
... On successful completion of this module, a student will be expected to be able to: Lower order : 30% - understand the basic principles related to modern physics, which includes relativity, matter waves, energy quantisation, x-ray and also laser generation, and the nuclear structure Middle orde ...
Module code SP-2306 Module Title Condensed Matter Physics
... On successful completion of this module, a student will be expected to be able to: Lower order : 30% - Identify crystal structures of solids, and explain electronic band structures. - Understand the theory on free electron model and models of heat capacity in solids. Middle order : 60% - ana ...
... On successful completion of this module, a student will be expected to be able to: Lower order : 30% - Identify crystal structures of solids, and explain electronic band structures. - Understand the theory on free electron model and models of heat capacity in solids. Middle order : 60% - ana ...
The 1/N expansion method in quantum field theory
... In perturbation theory, when calculating radiative corrections, one usually finds powers of the quantity λ2 ln(p2/M 2), where p is a representative of the momenta of the external particles. Even if λ is chosen small, at high energies, i.e., at large values of p, the logarithm may become large enough ...
... In perturbation theory, when calculating radiative corrections, one usually finds powers of the quantity λ2 ln(p2/M 2), where p is a representative of the momenta of the external particles. Even if λ is chosen small, at high energies, i.e., at large values of p, the logarithm may become large enough ...
- Physics
... What is the principle of Galilean relativity? Did Einstein accept it? What is the "ether?" Who attempted to measure its presence? ...
... What is the principle of Galilean relativity? Did Einstein accept it? What is the "ether?" Who attempted to measure its presence? ...
Renormalization group

In theoretical physics, the renormalization group (RG) refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales. In particle physics, it reflects the changes in the underlying force laws (codified in a quantum field theory) as the energy scale at which physical processes occur varies, energy/momentum and resolution distance scales being effectively conjugate under the uncertainty principle (cf. Compton wavelength).A change in scale is called a ""scale transformation"". The renormalization group is intimately related to ""scale invariance"" and ""conformal invariance"", symmetries in which a system appears the same at all scales (so-called self-similarity). (However, note that scale transformations are included in conformal transformations, in general: the latter including additional symmetry generators associated with special conformal transformations.)As the scale varies, it is as if one is changing the magnifying power of a notional microscope viewing the system. In so-called renormalizable theories, the system at one scale will generally be seen to consist of self-similar copies of itself when viewed at a smaller scale, with different parameters describing the components of the system. The components, or fundamental variables, may relate to atoms, elementary particles, atomic spins, etc. The parameters of the theory typically describe the interactions of the components. These may be variable ""couplings"" which measure the strength of various forces, or mass parameters themselves. The components themselves may appear to be composed of more of the self-same components as one goes to shorter distances.For example, in quantum electrodynamics (QED), an electron appears to be composed of electrons, positrons (anti-electrons) and photons, as one views it at higher resolution, at very short distances. The electron at such short distances has a slightly different electric charge than does the ""dressed electron"" seen at large distances, and this change, or ""running,"" in the value of the electric charge is determined by the renormalization group equation.