Non Euclidean Geometry
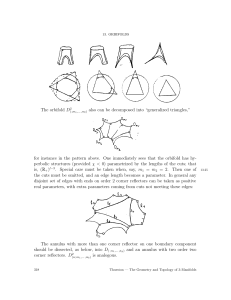
... meet. It is easy to convince yourself though that on the sphere any two great circles will intersect in two points. This means that one the sphere is not possible to draw parallel lines. They simply do NOT exist. This causes all kinds of problems for the theory of polygons. One obvious problem is th ...
... meet. It is easy to convince yourself though that on the sphere any two great circles will intersect in two points. This means that one the sphere is not possible to draw parallel lines. They simply do NOT exist. This causes all kinds of problems for the theory of polygons. One obvious problem is th ...
Answer
... The sum of the measures of five interior angles of a heptagon is 690. The measure of the 6th angle is twice the measure of the seventh. Find the measure of the 6th angle. Answer ...
... The sum of the measures of five interior angles of a heptagon is 690. The measure of the 6th angle is twice the measure of the seventh. Find the measure of the 6th angle. Answer ...
Math Circle Beginners Group May 8, 2016 Geometry
... 1. “In 1932, I was as old as the last two digits of my birth year. When I mentioned this interesting coincidence to my grandfather, he surprised me by saying that the same applied to him also. I thought that was impossible...” “Of course that’s possible,” a young woman said. “Believe me, it’s quite ...
... 1. “In 1932, I was as old as the last two digits of my birth year. When I mentioned this interesting coincidence to my grandfather, he surprised me by saying that the same applied to him also. I thought that was impossible...” “Of course that’s possible,” a young woman said. “Believe me, it’s quite ...
Math 2AB
... your own words to help you determine if a shape is a polygon. A polygon is a plane figure … 1) Formed by three or more line segments called sides. ...
... your own words to help you determine if a shape is a polygon. A polygon is a plane figure … 1) Formed by three or more line segments called sides. ...
Definition of Polygon
... Notice in each case before this the polygon is separated into triangles. The sum of the measures of the angles of each polygon can be found by adding the measures of the angles of the triangles. This is easy to find since the sum of the angles in a triangle = ______. Use the chart below to find a ...
... Notice in each case before this the polygon is separated into triangles. The sum of the measures of the angles of each polygon can be found by adding the measures of the angles of the triangles. This is easy to find since the sum of the angles in a triangle = ______. Use the chart below to find a ...
Unit 13 - Connecticut Core Standards
... the relationship between a conditional statement and its converse. In addition, the converse is used to justify the compass and straightedge construction of a line through a given point parallel to a given line. Regular polygons are studied in Investigation 4. Students learn how to use compass and s ...
... the relationship between a conditional statement and its converse. In addition, the converse is used to justify the compass and straightedge construction of a line through a given point parallel to a given line. Regular polygons are studied in Investigation 4. Students learn how to use compass and s ...
Euclidean Geometry: A Review
... points in the plane lie exactly on a line. What happens when we add a third point? Well, they may be collinear or they may not be collinear. If you take three noncollinear points in the plane, you can draw lines between them to produce a triangle. How do we classify triangles? We classify triangles ...
... points in the plane lie exactly on a line. What happens when we add a third point? Well, they may be collinear or they may not be collinear. If you take three noncollinear points in the plane, you can draw lines between them to produce a triangle. How do we classify triangles? We classify triangles ...
Calculating angles - Pearson Schools and FE Colleges
... A regular shape has all sides of equal length and all angles equal. Look at this regular pentagon. The interior angles are all 108° and the exterior angles are all 72°. Imagine the pentagon as a path. At each vertex there is a change of direction. By walking around the complete polygon so that you f ...
... A regular shape has all sides of equal length and all angles equal. Look at this regular pentagon. The interior angles are all 108° and the exterior angles are all 72°. Imagine the pentagon as a path. At each vertex there is a change of direction. By walking around the complete polygon so that you f ...
Polygon
... Polygon: A closed figure with straight sides and does not have any lines that cross through the middle. Thumbs: Polygons or Not Polygons? ...
... Polygon: A closed figure with straight sides and does not have any lines that cross through the middle. Thumbs: Polygons or Not Polygons? ...
euclidean parallel postulate
... written ∆ABC ~ ∆DEF , when all three pairs of corresponding angles are congruent and the lengths of all three pairs of corresponding sides are proportional. To establish similarity of triangles, however, it is not necessary to establish congruence of all pairs of angles and proportionality of all p ...
... written ∆ABC ~ ∆DEF , when all three pairs of corresponding angles are congruent and the lengths of all three pairs of corresponding sides are proportional. To establish similarity of triangles, however, it is not necessary to establish congruence of all pairs of angles and proportionality of all p ...
Glossary*Honors Geometry
... **Undefined Terms – Terms whose general meaning is assumed and whose characteristics are understood only from the postulates or axioms that use them. ...
... **Undefined Terms – Terms whose general meaning is assumed and whose characteristics are understood only from the postulates or axioms that use them. ...
content domain geometry propoerties of shape
... reference Year 1 1G1a Recognise and name common 2-D shapes [e.g.: rectangles (including squares), circles and triangles] ...
... reference Year 1 1G1a Recognise and name common 2-D shapes [e.g.: rectangles (including squares), circles and triangles] ...
QUADRILATERALS This handout concerns properties of
... MATH 410. SPRING 2007. INSTRUCTOR: PROFESSOR AITKEN ...
... MATH 410. SPRING 2007. INSTRUCTOR: PROFESSOR AITKEN ...
similar polygons
... in centimeters. The rectangular model of the racing car is similar to the rectangular racing car, so the corresponding lengths are ...
... in centimeters. The rectangular model of the racing car is similar to the rectangular racing car, so the corresponding lengths are ...
Exterior Angles
... Angles in a triangle • Sum of angles in a triangle: Adding all the angles in a triangle gives 180°. • Remote Interior angles of a triangle: The two non adjacent angles to the exterior angle. • Exterior angle inequality: An exterior angle of a triangle is greater than either of the remote interior ...
... Angles in a triangle • Sum of angles in a triangle: Adding all the angles in a triangle gives 180°. • Remote Interior angles of a triangle: The two non adjacent angles to the exterior angle. • Exterior angle inequality: An exterior angle of a triangle is greater than either of the remote interior ...
Answer - Imagine School at Lakewood Ranch
... Answer: Ana moved 2 places right and 2 places up. So, the translation can be written (2, 2). ...
... Answer: Ana moved 2 places right and 2 places up. So, the translation can be written (2, 2). ...
Regular polytope
In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces (for all 0 ≤ j ≤ n, where n is the dimension of the polytope) — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of dimension ≤ n. Regular polytopes are the generalized analog in any number of dimensions of regular polygons (for example, the square or the regular pentagon) and regular polyhedra (for example, the cube). The strong symmetry of the regular polytopes gives them an aesthetic quality that interests both non-mathematicians and mathematicians.Classically, a regular polytope in n dimensions may be defined as having regular facets [(n − 1)-faces] and regular vertex figures. These two conditions are sufficient to ensure that all faces are alike and all vertices are alike. Note, however, that this definition does not work for abstract polytopes.A regular polytope can be represented by a Schläfli symbol of the form {a, b, c, ...., y, z}, with regular facets as {a, b, c, ..., y}, and regular vertex figures as {b, c, ..., y, z}.