TestID 32339 09-12 Geometry DIA – Study Guide G.8.4 and D.6.2
... Which statement is the contrapostive of "If a quadrilateral is a square, then it has four right angles"? A. If a quadrilateral is not a square, then it has four right angles. B. If a quadrilateral does not have four right angles, then it is not a square. C. If a quadrilateral is not a square, then i ...
... Which statement is the contrapostive of "If a quadrilateral is a square, then it has four right angles"? A. If a quadrilateral is not a square, then it has four right angles. B. If a quadrilateral does not have four right angles, then it is not a square. C. If a quadrilateral is not a square, then i ...
Geometry
... amount of space that it takes up) and capacity, which is the amount that it contains. ...
... amount of space that it takes up) and capacity, which is the amount that it contains. ...
10.2 Diagonals and Angle Measure
... 4. What is the measure of the exterior angles of a polygon? Activity: Have three come up and each hold a point in a length of yarn. Teacher explains the measure of the external angles of a polygon is from the direction on one side of the polygon to the direction of the next leg or side. Can be tho ...
... 4. What is the measure of the exterior angles of a polygon? Activity: Have three come up and each hold a point in a length of yarn. Teacher explains the measure of the external angles of a polygon is from the direction on one side of the polygon to the direction of the next leg or side. Can be tho ...
Lesson 10:Areas
... To learn the formula of the area of a regular polygon. To learn the formula of the area of a circle, of a circle sector and of an annulus. To apply adequately the formulae to find out the area of the more common plane figures. To know how to calculate the area or a composite figure. To know how to f ...
... To learn the formula of the area of a regular polygon. To learn the formula of the area of a circle, of a circle sector and of an annulus. To apply adequately the formulae to find out the area of the more common plane figures. To know how to calculate the area or a composite figure. To know how to f ...
Progression of GEOMETRY PROPERTIES OF SHAPE
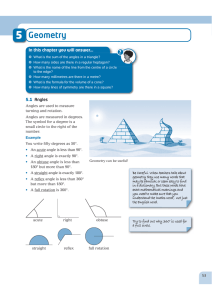
... Know angles are measured in degrees: estimate, compare acute, obtuse and reflex Draw given angles, and measure them in degrees (o) Identify: and one whole turn (total 360o) 1 a turn (total 180o) ...
... Know angles are measured in degrees: estimate, compare acute, obtuse and reflex Draw given angles, and measure them in degrees (o) Identify: and one whole turn (total 360o) 1 a turn (total 180o) ...
Regular Polygons
... - use the Point tool to place a point anywhere on the screen, not on the segment; - choose the arrow tool and select the point and the line segment; - then under the Construct menu choose Parallel Line. The parallel line should now be selected (colored) because it was the last object created. Under ...
... - use the Point tool to place a point anywhere on the screen, not on the segment; - choose the arrow tool and select the point and the line segment; - then under the Construct menu choose Parallel Line. The parallel line should now be selected (colored) because it was the last object created. Under ...
Angle Properties in Polygons
... Richard Buckminster “Bucky” Fuller (1895–1983) was an American architect and inventor who spent time working in Canada. He developed the geodesic dome and built a famous example, now called the Montréal Biosphere, for Expo 1967. A spin-off from Fuller’s dome design was the buckyball, which became th ...
... Richard Buckminster “Bucky” Fuller (1895–1983) was an American architect and inventor who spent time working in Canada. He developed the geodesic dome and built a famous example, now called the Montréal Biosphere, for Expo 1967. A spin-off from Fuller’s dome design was the buckyball, which became th ...
Polygons A polygon is a closed figure that is drawn on a plane. It
... The Polygon Exterior Angle-Sum Theorem is very helpful when trying to find the measure of the exterior angle of a regular polygon. Remember, regular polygons have all interior angles congruent. From this information, we can recognize that all exterior angles are also congruent. Often this knowledge ...
... The Polygon Exterior Angle-Sum Theorem is very helpful when trying to find the measure of the exterior angle of a regular polygon. Remember, regular polygons have all interior angles congruent. From this information, we can recognize that all exterior angles are also congruent. Often this knowledge ...
Math Background - Connected Mathematics Project
... An important distinction to keep in mind in geometric units is that a polygon consists of only the line segments (or sides) that make up the polygon. These line segments enclose a region of the flat surface. This region is sometimes called the interior of the polygon or polygonal region. The points ...
... An important distinction to keep in mind in geometric units is that a polygon consists of only the line segments (or sides) that make up the polygon. These line segments enclose a region of the flat surface. This region is sometimes called the interior of the polygon or polygonal region. The points ...
Chapter 2 - UT Mathematics
... as saying that, in area, the square built upon the hypotenuse of a right-angled triangle is equal to the sum of the squares built upon the other two sides. There are many proofs of Pythagoras’ theorem, some synthetic, some algebraic, and some visual as well as many combinations of these. Here you w ...
... as saying that, in area, the square built upon the hypotenuse of a right-angled triangle is equal to the sum of the squares built upon the other two sides. There are many proofs of Pythagoras’ theorem, some synthetic, some algebraic, and some visual as well as many combinations of these. Here you w ...
Regular polytope
In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces (for all 0 ≤ j ≤ n, where n is the dimension of the polytope) — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of dimension ≤ n. Regular polytopes are the generalized analog in any number of dimensions of regular polygons (for example, the square or the regular pentagon) and regular polyhedra (for example, the cube). The strong symmetry of the regular polytopes gives them an aesthetic quality that interests both non-mathematicians and mathematicians.Classically, a regular polytope in n dimensions may be defined as having regular facets [(n − 1)-faces] and regular vertex figures. These two conditions are sufficient to ensure that all faces are alike and all vertices are alike. Note, however, that this definition does not work for abstract polytopes.A regular polytope can be represented by a Schläfli symbol of the form {a, b, c, ...., y, z}, with regular facets as {a, b, c, ..., y}, and regular vertex figures as {b, c, ..., y, z}.