Geometry 202
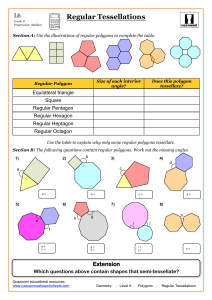
... A regular tessellation is a tessellation formed by only one type of regular polygon. Tessellations with Specific Attributes If a tessellation contains the same arrangement of shapes and angles at each vertex it is uniform. A uniform tessellation formed using two or more regular polygons is a semi-re ...
... A regular tessellation is a tessellation formed by only one type of regular polygon. Tessellations with Specific Attributes If a tessellation contains the same arrangement of shapes and angles at each vertex it is uniform. A uniform tessellation formed using two or more regular polygons is a semi-re ...
Regular polyhedra
... Regular polyhedra An investigation by Laura Escobar Math Explorer’s Club, Nov. 3, 2012 ...
... Regular polyhedra An investigation by Laura Escobar Math Explorer’s Club, Nov. 3, 2012 ...
Handout - University of Toronto
... A polygon is a region of the plane whose border is a path made up of straight line segments which only touch at endpoints (called vertices). A regular polygon has all its sides the same length and the angles are all the same. These are the most commonly encountered types by students and tend to have ...
... A polygon is a region of the plane whose border is a path made up of straight line segments which only touch at endpoints (called vertices). A regular polygon has all its sides the same length and the angles are all the same. These are the most commonly encountered types by students and tend to have ...
Platonic Solids - hrsbstaff.ednet.ns.ca
... only two came together they would collapse against one another and we would not get a solid. Second, observe that the sum of the interior angles of the faces meeting at each vertex must be less than 360°, for otherwise they would not all fit together. Now, each interior angle of an equilateral trian ...
... only two came together they would collapse against one another and we would not get a solid. Second, observe that the sum of the interior angles of the faces meeting at each vertex must be less than 360°, for otherwise they would not all fit together. Now, each interior angle of an equilateral trian ...
Regular polytope
In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces (for all 0 ≤ j ≤ n, where n is the dimension of the polytope) — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of dimension ≤ n. Regular polytopes are the generalized analog in any number of dimensions of regular polygons (for example, the square or the regular pentagon) and regular polyhedra (for example, the cube). The strong symmetry of the regular polytopes gives them an aesthetic quality that interests both non-mathematicians and mathematicians.Classically, a regular polytope in n dimensions may be defined as having regular facets [(n − 1)-faces] and regular vertex figures. These two conditions are sufficient to ensure that all faces are alike and all vertices are alike. Note, however, that this definition does not work for abstract polytopes.A regular polytope can be represented by a Schläfli symbol of the form {a, b, c, ...., y, z}, with regular facets as {a, b, c, ..., y}, and regular vertex figures as {b, c, ..., y, z}.