How are the formulas for area of figures derived and applied to solve
... Concept: Area of Polygons base height center of a regular polygon radius of a regular polygon apothem central angles composite figures Concept: Circumference and Area of Circles and Sectors sectors of a circle segment of a circle - ...
... Concept: Area of Polygons base height center of a regular polygon radius of a regular polygon apothem central angles composite figures Concept: Circumference and Area of Circles and Sectors sectors of a circle segment of a circle - ...
360 a b c d e + + + + = ( 2) 180 N Θ =
... circumscribed by circles. As N becomes large, the polygon will tend to a circle and hence all three shapes will coalesce. ...
... circumscribed by circles. As N becomes large, the polygon will tend to a circle and hence all three shapes will coalesce. ...
4.2 Tilings INSTRUCTOR NOTES
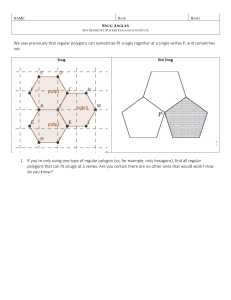
... (number of polygons) = 360°/(angle measure) For example, in a tiling for regular hexagons we have each vertex surrounded by 3 regular hexagons because (number of polygons) = 360°/120° = 3. However, note that the “number of polygons” must be an integer. Looking at the table at the beginning and runni ...
... (number of polygons) = 360°/(angle measure) For example, in a tiling for regular hexagons we have each vertex surrounded by 3 regular hexagons because (number of polygons) = 360°/120° = 3. However, note that the “number of polygons” must be an integer. Looking at the table at the beginning and runni ...
1 Appendix to notes 2, on Hyperbolic geometry:
... De…nition: A “line”is any diameter of this disk, or the set of points on a circle which intersects D and which meets the boundary of D in two places and at right angles to the boundary of D at both of these places. Notice that a diameter can be considered part of such a circle of in…nite radius. How ...
... De…nition: A “line”is any diameter of this disk, or the set of points on a circle which intersects D and which meets the boundary of D in two places and at right angles to the boundary of D at both of these places. Notice that a diameter can be considered part of such a circle of in…nite radius. How ...
Platonic Solids
... The 5 platonic solids are: Definition: The most basic definition is to say that a Platonic Solid is an object where all faces are identical and the same number of faces meet at each vertex. In solid geometry and some ancient physical theories, a Platonic solid is a convex polyhedron with all its fac ...
... The 5 platonic solids are: Definition: The most basic definition is to say that a Platonic Solid is an object where all faces are identical and the same number of faces meet at each vertex. In solid geometry and some ancient physical theories, a Platonic solid is a convex polyhedron with all its fac ...
Triangles and Squares
... Use Poincaré model of the same polytope to measure its dihedral angles Dihedrals are well-defined at finite hyperbolic points on incenter of each 2-face Invariant since projective transformations correspond to hyperbolic isometries Gluing is convex iff sum of dihedrals is less than 180 degrees Can a ...
... Use Poincaré model of the same polytope to measure its dihedral angles Dihedrals are well-defined at finite hyperbolic points on incenter of each 2-face Invariant since projective transformations correspond to hyperbolic isometries Gluing is convex iff sum of dihedrals is less than 180 degrees Can a ...
14. regular polyhedra and spheres
... Making polyhedra from other regular polygons The corners of a 4-sided regular polygon Sum of the angles of a quadrilateral = 360° If it is regular, the size of each angle = 360° ÷ 4 = 90°. A solid in which 3 square faces meet at each vertex is called a cube. A cube has: 6 faces, 8 vertices, 3 faces ...
... Making polyhedra from other regular polygons The corners of a 4-sided regular polygon Sum of the angles of a quadrilateral = 360° If it is regular, the size of each angle = 360° ÷ 4 = 90°. A solid in which 3 square faces meet at each vertex is called a cube. A cube has: 6 faces, 8 vertices, 3 faces ...
2_M2306_Hist_chapter2
... common notions) • Euclid often made use of visually plausible assumptions that are not among the postulates • 17th century – development of analytic geometry (Descartes) • 5th postulate – the parallel axiom • 19th century: non-Euclidean geometries ...
... common notions) • Euclid often made use of visually plausible assumptions that are not among the postulates • 17th century – development of analytic geometry (Descartes) • 5th postulate – the parallel axiom • 19th century: non-Euclidean geometries ...
DA 10 GE 12_0 Review
... GE 12.0* Students find and use measures of sides and of interior and exterior angles of ...
... GE 12.0* Students find and use measures of sides and of interior and exterior angles of ...
Word Problems
... regular polygon. In order for the boxes to pack tightly, she decides to use a regular polygon that has the property that the measure of its interior angles is half the measure of its exterior angles. What regular polygon should she use? ...
... regular polygon. In order for the boxes to pack tightly, she decides to use a regular polygon that has the property that the measure of its interior angles is half the measure of its exterior angles. What regular polygon should she use? ...
Regular polytope
In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces (for all 0 ≤ j ≤ n, where n is the dimension of the polytope) — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of dimension ≤ n. Regular polytopes are the generalized analog in any number of dimensions of regular polygons (for example, the square or the regular pentagon) and regular polyhedra (for example, the cube). The strong symmetry of the regular polytopes gives them an aesthetic quality that interests both non-mathematicians and mathematicians.Classically, a regular polytope in n dimensions may be defined as having regular facets [(n − 1)-faces] and regular vertex figures. These two conditions are sufficient to ensure that all faces are alike and all vertices are alike. Note, however, that this definition does not work for abstract polytopes.A regular polytope can be represented by a Schläfli symbol of the form {a, b, c, ...., y, z}, with regular facets as {a, b, c, ..., y}, and regular vertex figures as {b, c, ..., y, z}.