Download 2_M2306_Hist_chapter2

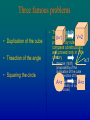
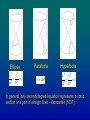
Chapter 2
Greek Geometry
•
•
•
•
•
•
The Deductive Method
The Regular Polyhedra
Ruler and Compass Construction
Conic Sections
Higher-degree curves
Biographical Notes: Euclid
2.1 The Deductive Method
• The most evident possible statements:
Axioms
• New statements (theorems, propositions etc.)
can be derived from axioms and statements
already established statements using evident
principles of logic
Originator of the method: Thales (624 – 547 BCE)
Euclid’s “Elements”
( ≈ 300 BCE)
Postulates
Common Notions
Axioms
Principles of logic
Postulates
1. To draw a straight line from any point to any point
2. To produce a finite straight line continuously in a
straight line
3. To describe a circle with any centre and distance
4. That all right angles are equal to one another
5. That if a straight line falling on two straight lines make
the interior angles on the same side less than two right
angles, the two straight lines, if produced indefinitely,
meet on that side on which are the angles less than the
two right angles
Common Notions
1. Things which are equal to the same thing are also equal
to one another
2. If equals be added to equals, the wholes are equal
3. If equals be subtracted from equals, the remainders are
equal
4. Things which coincide with one another are equal to
one another
5. The whole is grater than the part
Remarks
• The intention was to deduce geometric
propositions from visually evident statements
(postulates) using evident principles of logic (the
common notions)
• Euclid often made use of visually plausible
assumptions that are not among the postulates
• 17th century – development of analytic geometry
(Descartes)
• 5th postulate – the parallel axiom
• 19th century: non-Euclidean geometries
2.2 The Regular Polyhedra
Definition A polyhedron which is bounded by
a number of congruent polygonal faces,
so that the same number of faces meet at each
vertex, and in each face all the sides and angles
are equal (i.e. faces are regular polygons) is called
the regular polyhedron
Regular polygon: any number n > 2 of sides
Regular polyhedron: only five!
5 Regular Polyhedra
(The Platonic Solids)
Four Elements
Proof
Consider polygons that can occur as faces
The sum of angles with common vertex must
be less than 2 π = 360o
Number of
sides n
3
Angle
4
π/2
Max. number of
faces
5
(3,4, or 5)
3
5
3π / 5
3
6
(and more)
≥ 2π / 3
Impossible
π/3
Construction of Icosahedron
(by Luca Pacioli, 1509)
3 golden rectangles (with sides 1 and (1+√5) /2 )
AD = (1+√5) /2 )
A
BC = 1
B
C
D
AB = AC = BC =1
Icosahedron and Dodecahedron
Spheres
• For every regular polyhedron there exist
the sphere which passes through all its
vertices (its radius is called
circumradius) and the sphere which
touches all its faces (its radius is called
inradius)
Kepler’s diagram of the polyhedra
• Johannes Kepler (1571 – 1630) – great
astronomer
• Three Laws of planetary motion
• Kepler’s theory of planetary distances
(based on regular polyhedra)
• The theory was ruined when Uranus
was discovered in 1781
Kepler’s diagram of the polyhedra
2.3 Ruler and Compass
Constructions
•
The ruler and compass elementary operations:
–
–
–
•
•
given two points, construct the line through them
given two points, construct the circle centered at one point passing
through the other point
given two lines, two circles, or a line and a circle, construct their
intersection points
A point P is called constructible from points P1, P2, … , Pn, if P can
be obtained from these points with a finite sequence of elementary
operations
One can show that the points constructible from P1, P2, … , Pn are
precisely the points which have coordinates in the set of numbers
generated from the coordinates of P1, P2, … , Pn by the operations
+, -, *, / , and √
Three famous problems
• Duplication of the cube
• Trisection of the angle
• Squaring the circle
• The impossibility of
solving
V=1 of these V=2
problems by ruler and
compass constructions
was proved only in 19th
α
century
α/3
– Wantzel (1837)
(impossiblity of the
duplication of the cube
and trisection of the angle)
– A=π
Lindemann (1882) A=π
(impossibility of squaring
of the circle)
Equivalent form
• Starting from the unit length, it is
impossible to construct
– 3√2 (duplication of the cube)
– π (squaring the circle)
– sin 20o (trisection of the angle α = 60o)
Open problem
• Which regular n-gons are constructible?
• Equivalent problem: circle division
• Gauss (1796): 17-gon is constructible and a regular
n-gon is constructible if and only if
n = 2mp1p2…pk, where each pi is a prime of the form
h
22 + 1 (Fermat prime)
• What are these primes?
• Are there infinitely many of these primes? (the only
known are for h=0,1,2,3,4 (3, 5, 17, 257, and 65537))
2.4 Conic Sections
Ellipse
x2 y2
 2 1
2
a
b
Parabola
Hyperbola
y  ax 2
x2 y2
 2 1
2
a
b
In general, any second-degree equation represents a conic
section or a pair of straight lines – Descartes (1637)
Menaechmus
th
(4
century BCE)
• Invention of conic sections
• Used conic sections to solve the problem of
duplication of the cube
(finding the intersection of parabola with
hyperbola)
1 2
Consider t he intersecti on of parabola y  x
2
with hyperbola xy  1 :
1 2
x x  1  x3  2
2
Drawing of conic sections
Generalized compass
described by the Arab
mathematician
al-Kuji (around 1000 CE)
Application of conic sections
• Kepler (1609): the orbits of planets are ellipses
• Newton (1687) explained this fact by his law of
gravitation
2.5 Higher-degree Curves
• There was no systematic theory of
higher-degree curves in Greek
mathematics
• Greeks studied many interesting special
cases
– The Cissoid of Diocles ( ≈ 100 BCE)
– The Spiric Sections of Perseus (≈ 150 BCE)
– The Epicycles of Ptolemy ( ≈ 140 CE)
The Cissoid of Diocles ( ≈ 100 BCE)
Cubic curve with
Cartesian equation
y2 (1+x) = (1-x)3
Diocles showed that the
cissoid could be used
to duplicate the cube
The Spiric Sections of Perseus
• Torus (or Spira) – one of the surfaces studied by
Greeks
• Spiric section – the section of torus by plane parallel
to the axis of the torus
• Curves of degree 4
Cassini oval
Lemniscate
of Bernoulli
The Epicycles of Ptolemy
• Almagest – astronomical work of
Claudius Ptolemy
• Epicycles were candidates for the
planetary orbits
P
2.6 Biographical Notes: Euclid
• Taught in Alexandria
(around 300 BCE)
• “There is no royal road in
geometry”
• “Elements”
Euclid