Regular polygons
... Obtuse: one angle in a triangle is greater than 90˚ Remember that there can only be one angle greater than 90˚ in a triangle Scalene: no sides are congruent Isosceles: two sides congruent Equilateral: all sides congruent Equiangular: all angles congruent Equilateral triangles are regular polygon ...
... Obtuse: one angle in a triangle is greater than 90˚ Remember that there can only be one angle greater than 90˚ in a triangle Scalene: no sides are congruent Isosceles: two sides congruent Equilateral: all sides congruent Equiangular: all angles congruent Equilateral triangles are regular polygon ...
Study Guide - page under construction
... • If a quadrilateral is an isosceles trapezoid, then each pair of base angles are congruent. • If a trapezoid has one pair of congruent base angles, then it is an isosceles triangle. • A trapezoid is isosceles if and only if its diagonals are congruent. • Trapezoid Midsegment Theorem - The midsegmen ...
... • If a quadrilateral is an isosceles trapezoid, then each pair of base angles are congruent. • If a trapezoid has one pair of congruent base angles, then it is an isosceles triangle. • A trapezoid is isosceles if and only if its diagonals are congruent. • Trapezoid Midsegment Theorem - The midsegmen ...
Review for Polygon Test
... 16.__________ The diagonals of a rectangle bisect the angles of the rectangle. 17.__________ The diagonals of a rectangle are perpendicular to each other. 18.__________ The four angles of a trapezoid are congruent. 19.__________ The diagonals of a rhombus are perpendicular. 20.__________ A rhombus i ...
... 16.__________ The diagonals of a rectangle bisect the angles of the rectangle. 17.__________ The diagonals of a rectangle are perpendicular to each other. 18.__________ The four angles of a trapezoid are congruent. 19.__________ The diagonals of a rhombus are perpendicular. 20.__________ A rhombus i ...
Unit 1 | Similarity, Congruence, and Proofs
... of its sides are divided proportionally, the line is parallel to the third side of the triangle. Use triangle similarity to prove the Pythagorean Theorem. ...
... of its sides are divided proportionally, the line is parallel to the third side of the triangle. Use triangle similarity to prove the Pythagorean Theorem. ...
7.2 Lesson
... 2. The ratio of a model sailboat’s dimensions to the actual boat’s dimensions is . If the length of the model is 10 inches, what is the length of the actual sailboat in feet? ...
... 2. The ratio of a model sailboat’s dimensions to the actual boat’s dimensions is . If the length of the model is 10 inches, what is the length of the actual sailboat in feet? ...
Exterior Angle Theorem from 4.1 1 A B C
... Polygon Exterior Angles Theorem The sum of the measures of the exterior angles of a convex polygon, one angle at each vertex is 360. ...
... Polygon Exterior Angles Theorem The sum of the measures of the exterior angles of a convex polygon, one angle at each vertex is 360. ...
Sum of Interior and Exterior Angles in Polygons
... Draw a quadrilateral and extend the sides. There are two sets of angles formed when the sides of a polygon are extended. • The original angles are called interior angles. • The angles that are adjacent to the interior angles are called exterior angles. ...
... Draw a quadrilateral and extend the sides. There are two sets of angles formed when the sides of a polygon are extended. • The original angles are called interior angles. • The angles that are adjacent to the interior angles are called exterior angles. ...
Sum of Interior and Exterior Angles in Polygons
... Draw a quadrilateral and extend the sides. There are two sets of angles formed when the sides of a polygon are extended. • The original angles are called interior angles. • The angles that are adjacent to the interior angles are called exterior angles. ...
... Draw a quadrilateral and extend the sides. There are two sets of angles formed when the sides of a polygon are extended. • The original angles are called interior angles. • The angles that are adjacent to the interior angles are called exterior angles. ...
Sum of Interior and Exterior Angles in Polygons
... Draw a quadrilateral and extend the sides. There are two sets of angles formed when the sides of a polygon are extended. • The original angles are called interior angles. • The angles that are adjacent to the interior angles are called exterior angles. ...
... Draw a quadrilateral and extend the sides. There are two sets of angles formed when the sides of a polygon are extended. • The original angles are called interior angles. • The angles that are adjacent to the interior angles are called exterior angles. ...
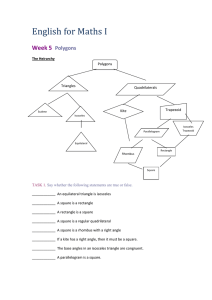
English for Maths I
... In geometry a polygon is traditionally ………………..that is bounded by a finite chain of straight………………… closing in a loop to form a closed chain or ……………….. These segments are called its edges or sides, and the points where two edges meet are the polygon's vertices (singular: vertex) or………………. The inter ...
... In geometry a polygon is traditionally ………………..that is bounded by a finite chain of straight………………… closing in a loop to form a closed chain or ……………….. These segments are called its edges or sides, and the points where two edges meet are the polygon's vertices (singular: vertex) or………………. The inter ...
NYS Mathematics Glossary* – Geometry
... absolute value The distance from 0 to a number n on a number line. The absolute value of a number n is indicated by n . Example: −3 = 3 , +3 = 3 , and 0 = 0 . acute angle An angle whose measure is greater than 0° and less than 90°. acute triangle A triangle that contains three acute angles. additive ...
... absolute value The distance from 0 to a number n on a number line. The absolute value of a number n is indicated by n . Example: −3 = 3 , +3 = 3 , and 0 = 0 . acute angle An angle whose measure is greater than 0° and less than 90°. acute triangle A triangle that contains three acute angles. additive ...
MATH 310 ! Self-Test " Transformation Geometry
... 7b. There are five line symmetries of the regular pentagon, one from each vertex through the midpoint of the opposite side. There are also five rotational symmetries of the regular pentagon; the smallest is one-fifth of a rotation, 72E; the other four are, of course, 144E, 216E, 288E and 360E. The c ...
... 7b. There are five line symmetries of the regular pentagon, one from each vertex through the midpoint of the opposite side. There are also five rotational symmetries of the regular pentagon; the smallest is one-fifth of a rotation, 72E; the other four are, of course, 144E, 216E, 288E and 360E. The c ...
Notes on transformational geometry
... ψ preserve distance, then so does ψ ◦ φ. Let X, Y be any two points and let X 0 = φ(X), Y 0 = φ(Y ), X 00 = ψ(X 0 ), Y 00 = ψ(Y 0 ). Then XY = X 0 Y 0 (because φ is an isometry) and X 0 Y 0 = X 00 Y 00 (because ψ is an isometry), but that means that XY = X 00 Y 00 , and X 00 = (ψ ◦ φ)(X) and Y 00 = ...
... ψ preserve distance, then so does ψ ◦ φ. Let X, Y be any two points and let X 0 = φ(X), Y 0 = φ(Y ), X 00 = ψ(X 0 ), Y 00 = ψ(Y 0 ). Then XY = X 0 Y 0 (because φ is an isometry) and X 0 Y 0 = X 00 Y 00 (because ψ is an isometry), but that means that XY = X 00 Y 00 , and X 00 = (ψ ◦ φ)(X) and Y 00 = ...
Shapes Chapter 16 Polyhedra
... drawing). There is no single kind of drawing for a three-dimensional shape, unfortunately. You will see “perspective” drawings, like Figure 1 below, which attempt to be close to how the eye might see the object. Some segments that are actually parallel in the shape may appear to converge in the draw ...
... drawing). There is no single kind of drawing for a three-dimensional shape, unfortunately. You will see “perspective” drawings, like Figure 1 below, which attempt to be close to how the eye might see the object. Some segments that are actually parallel in the shape may appear to converge in the draw ...
Chap 4 homework packet
... 2.) If two angles in one triangle are congruent to two angles in another triangle then A. The triangles are equilateral. B. The triangles are congruent C. The third angles in both triangles are congruent D. The third angles in both triangles are not congruent E. The angles are acute. ...
... 2.) If two angles in one triangle are congruent to two angles in another triangle then A. The triangles are equilateral. B. The triangles are congruent C. The third angles in both triangles are congruent D. The third angles in both triangles are not congruent E. The angles are acute. ...
similar polygons
... Ratios in Similar Polygons A similarity ratio is the ratio of the lengths of the corresponding sides of two similar polygons. The similarity ratio of ∆ABC to ∆DEF is __2:1_____. The similarity ratio of ∆DEF to ∆ABC is __1:2_____. ...
... Ratios in Similar Polygons A similarity ratio is the ratio of the lengths of the corresponding sides of two similar polygons. The similarity ratio of ∆ABC to ∆DEF is __2:1_____. The similarity ratio of ∆DEF to ∆ABC is __1:2_____. ...
Regular polytope
In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces (for all 0 ≤ j ≤ n, where n is the dimension of the polytope) — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of dimension ≤ n. Regular polytopes are the generalized analog in any number of dimensions of regular polygons (for example, the square or the regular pentagon) and regular polyhedra (for example, the cube). The strong symmetry of the regular polytopes gives them an aesthetic quality that interests both non-mathematicians and mathematicians.Classically, a regular polytope in n dimensions may be defined as having regular facets [(n − 1)-faces] and regular vertex figures. These two conditions are sufficient to ensure that all faces are alike and all vertices are alike. Note, however, that this definition does not work for abstract polytopes.A regular polytope can be represented by a Schläfli symbol of the form {a, b, c, ...., y, z}, with regular facets as {a, b, c, ..., y}, and regular vertex figures as {b, c, ..., y, z}.