Chapter 9 Geometric Properties (2013)
... 1. You are assigned to a team. Your team MUST be together (within sight of each other) at all times. There is enough work so that all members of your team can be actively involved. An example of how to divide up work is shown below: A. One person in charge of the camera B. One person in charge of vo ...
... 1. You are assigned to a team. Your team MUST be together (within sight of each other) at all times. There is enough work so that all members of your team can be actively involved. An example of how to divide up work is shown below: A. One person in charge of the camera B. One person in charge of vo ...
Verifiable Implementations of Geometric Algorithms
... form a triangle. On the right, the three lines pass through a single point C. This choice is possible because one can easily prove that there exists three nearby lines which are indeed concurrent at point C. (The diagram looks awkward because the error has been magnified so as to be visible.) An err ...
... form a triangle. On the right, the three lines pass through a single point C. This choice is possible because one can easily prove that there exists three nearby lines which are indeed concurrent at point C. (The diagram looks awkward because the error has been magnified so as to be visible.) An err ...
Chap 6 homework packet
... For 53-56, write the equation of each line described. 53.) The line passes through the point (-6, -2) 54.) The line passes through the point (8, -1) and is and is perpendicular to the line whose equation is parallel to the line whose equation is 3x + 2y = 8. 5x – 4y = 6. ...
... For 53-56, write the equation of each line described. 53.) The line passes through the point (-6, -2) 54.) The line passes through the point (8, -1) and is and is perpendicular to the line whose equation is parallel to the line whose equation is 3x + 2y = 8. 5x – 4y = 6. ...
Classifying Polygons
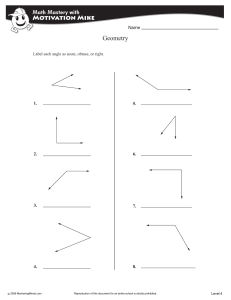
... Classifying by Angles Angles can be grouped by their angles; acute, obtuse or right. In any triangle, two of the angles will always be acute. The third angle can be acute, obtuse, or right. We classify each triangle by this angle. Right Triangle: A triangle with one right angle. ...
... Classifying by Angles Angles can be grouped by their angles; acute, obtuse or right. In any triangle, two of the angles will always be acute. The third angle can be acute, obtuse, or right. We classify each triangle by this angle. Right Triangle: A triangle with one right angle. ...
Polygons - cK-12
... Solution: The exterior angle and interior angle at the same vertex will always be supplementary because together they form a straight angle. In this case, the interior angle at point G was approximately 128.6◦ . Therefore, the exterior angle is 180◦ − 128.6◦ = 51.4◦ . Concept Problem Revisited There ...
... Solution: The exterior angle and interior angle at the same vertex will always be supplementary because together they form a straight angle. In this case, the interior angle at point G was approximately 128.6◦ . Therefore, the exterior angle is 180◦ − 128.6◦ = 51.4◦ . Concept Problem Revisited There ...
Algebra 1 GT Lesson Plan
... Construct midpoints of the three sides and call them L, M, and N. Label the points where the altitudes intersect the sides of triangle ABC, and call these R, S, and T. Construct the midpoints of AH, BH, and CH, and call them X, Y, and Z. Then L, M, N, R, S, T, X, Y, and Z are all on the same ...
... Construct midpoints of the three sides and call them L, M, and N. Label the points where the altitudes intersect the sides of triangle ABC, and call these R, S, and T. Construct the midpoints of AH, BH, and CH, and call them X, Y, and Z. Then L, M, N, R, S, T, X, Y, and Z are all on the same ...
11.3 Curves, Polygons and Symmetry
... A regular polygon is a polygon where all sides and interior angles are congruent. What is the name of a regular triangle? ...
... A regular polygon is a polygon where all sides and interior angles are congruent. What is the name of a regular triangle? ...
2.2 Angles Formed by Parallel Lines
... Try:If you are given one interior angle and one exterior angle of a triangle, can you always determine the other interior angles of the triangle? Explain, using diagrams. ...
... Try:If you are given one interior angle and one exterior angle of a triangle, can you always determine the other interior angles of the triangle? Explain, using diagrams. ...
Polygons - AGMath.com
... How many sides does it have? One vertex angle in a kite measures 57 degrees and one nonvertex angle measures 125 degrees. What are the measures of the other angles? An isosceles triangle has a perimeter of 42 inches, and has midpoints A, B, and C. If BC = 3 inches, what is the length of AB? The mids ...
... How many sides does it have? One vertex angle in a kite measures 57 degrees and one nonvertex angle measures 125 degrees. What are the measures of the other angles? An isosceles triangle has a perimeter of 42 inches, and has midpoints A, B, and C. If BC = 3 inches, what is the length of AB? The mids ...
Herbert Strutt Primary School – Numeracy Target Setting
... Plot specified points and draw sides to complete a given polygon. ...
... Plot specified points and draw sides to complete a given polygon. ...
MPM 1D - bell231
... What is the minimum number of angles you need to measure to calculate the measure of all of the interior and exterior angles of a quadrilateral? Justify your answer. 2. Draw an example of a quadrilateral with each of set of interior angles, or explain why the quadrilateral is not possible. ...
... What is the minimum number of angles you need to measure to calculate the measure of all of the interior and exterior angles of a quadrilateral? Justify your answer. 2. Draw an example of a quadrilateral with each of set of interior angles, or explain why the quadrilateral is not possible. ...
Geometry: Properties of Shapes IDENTIFYING SHAPES AND THIER
... use the properties of rectangles to deduce related facts and find missing lengths and angles distinguish between regular and irregular polygons based on reasoning about equal sides and angles ...
... use the properties of rectangles to deduce related facts and find missing lengths and angles distinguish between regular and irregular polygons based on reasoning about equal sides and angles ...
Camp 1 Lantern Packet
... (If polygon is regular, show calculation below. If not, carefully measure each angle) ...
... (If polygon is regular, show calculation below. If not, carefully measure each angle) ...
What`s in KnowRe`s Curricula?
... Third Angles Theorem Proving Polygons Congruent Corresponding Parts of Congruent Triangles are Congruent ...
... Third Angles Theorem Proving Polygons Congruent Corresponding Parts of Congruent Triangles are Congruent ...
Regular polytope
In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces (for all 0 ≤ j ≤ n, where n is the dimension of the polytope) — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of dimension ≤ n. Regular polytopes are the generalized analog in any number of dimensions of regular polygons (for example, the square or the regular pentagon) and regular polyhedra (for example, the cube). The strong symmetry of the regular polytopes gives them an aesthetic quality that interests both non-mathematicians and mathematicians.Classically, a regular polytope in n dimensions may be defined as having regular facets [(n − 1)-faces] and regular vertex figures. These two conditions are sufficient to ensure that all faces are alike and all vertices are alike. Note, however, that this definition does not work for abstract polytopes.A regular polytope can be represented by a Schläfli symbol of the form {a, b, c, ...., y, z}, with regular facets as {a, b, c, ..., y}, and regular vertex figures as {b, c, ..., y, z}.