File - LSL Math Weebly
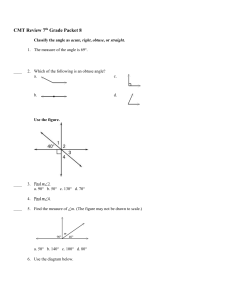
... 15. State the corresponding sides and angles in this pair of congruent triangles. ...
... 15. State the corresponding sides and angles in this pair of congruent triangles. ...
SS1 Classifying shapes
... Ask learners to share their criteria for sorting the shapes. Show how their four groups may be displayed using two-way tables. Help them to translate what they say into ‘official’ mathematical language such as: 앫 names of polygons (triangle, rhombus, regular etc.); 앫 names of angles (interior, exter ...
... Ask learners to share their criteria for sorting the shapes. Show how their four groups may be displayed using two-way tables. Help them to translate what they say into ‘official’ mathematical language such as: 앫 names of polygons (triangle, rhombus, regular etc.); 앫 names of angles (interior, exter ...
Atomic orbitals, symmetry, and coordination polyhedra
... Gillespie and Nyholm [2] which introduced the idea that the pairs of electrons in a valency shell, irrespective of whether they are shared (i.e., bonding) pairs or unshared (i.e., non-bonding) pairs, are always arranged in the same way which depends only on their number. Thus two pairs are arranged ...
... Gillespie and Nyholm [2] which introduced the idea that the pairs of electrons in a valency shell, irrespective of whether they are shared (i.e., bonding) pairs or unshared (i.e., non-bonding) pairs, are always arranged in the same way which depends only on their number. Thus two pairs are arranged ...
S1 Lines, angles and polygons
... When a line has end points we say that it has finite length. It is called a line segment. ...
... When a line has end points we say that it has finite length. It is called a line segment. ...
Geometry Policy - Churchfields Junior School
... Mathematical Vocabulary Children need to acquire appropriate vocabulary so that they can participate in the activities and lessons that are part of classroom life. There is, however, an even more important reason: mathematical language is crucial to children’s development of thinking. If children do ...
... Mathematical Vocabulary Children need to acquire appropriate vocabulary so that they can participate in the activities and lessons that are part of classroom life. There is, however, an even more important reason: mathematical language is crucial to children’s development of thinking. If children do ...
Polygon Angle-Sum Theorem - Mustang-Math
... Sketch polygons with 4, 5, 6, 7, and 8 sides on chart paper Divide into triangles by drawing diagonals from one vertex Multiply the # of Δ’s by 180 to find the polygon angle-sum # of Sides ...
... Sketch polygons with 4, 5, 6, 7, and 8 sides on chart paper Divide into triangles by drawing diagonals from one vertex Multiply the # of Δ’s by 180 to find the polygon angle-sum # of Sides ...
8 congruence, symmetry and similarity
... For two triangles to be congruent one of the following conditions of congruence must be true. The three sides of each triangle are equal (SSS). Two sides and the included angle are equal (SAS). Two angles and a corresponding side are equal (AAS). Each triangle contains a right angle, and the hypoten ...
... For two triangles to be congruent one of the following conditions of congruence must be true. The three sides of each triangle are equal (SSS). Two sides and the included angle are equal (SAS). Two angles and a corresponding side are equal (AAS). Each triangle contains a right angle, and the hypoten ...
Lecture
... You know that the angle-sum of a triangle is 180. With very little effort you can see that the same doesn’t hold true for a square. Just what is the angle-sum for a square? Do you remember Postulate 1-10? It says the area of a region is the sum of the areas of its non-overlapping regions. Now, it do ...
... You know that the angle-sum of a triangle is 180. With very little effort you can see that the same doesn’t hold true for a square. Just what is the angle-sum for a square? Do you remember Postulate 1-10? It says the area of a region is the sum of the areas of its non-overlapping regions. Now, it do ...
The Polygon Angle
... You know that the angle-sum of a triangle is 180. With very little effort you can see that the same doesn’t hold true for a square. Just what is the angle-sum for a square? Do you remember Postulate 1-10? It says the area of a region is the sum of the areas of its non-overlapping regions. Now, it do ...
... You know that the angle-sum of a triangle is 180. With very little effort you can see that the same doesn’t hold true for a square. Just what is the angle-sum for a square? Do you remember Postulate 1-10? It says the area of a region is the sum of the areas of its non-overlapping regions. Now, it do ...
Chapter 10: Two-Dimensional Figures
... Two-dimensional shapes are usually found in many real-world objects. The properties of two-dimensional figures can be used to solve real-world problems dealing with snowflakes. For example, if you know the exact shape of a snowflake, you can find the measure of an interior angle in a snowflake. You ...
... Two-dimensional shapes are usually found in many real-world objects. The properties of two-dimensional figures can be used to solve real-world problems dealing with snowflakes. For example, if you know the exact shape of a snowflake, you can find the measure of an interior angle in a snowflake. You ...
Unit 7 – Polygons and Circles Diagonals of a Polygon
... Participants will now investigate the exterior angles of a polygon. It is often difficult for students to understand intuitively that this sum does not depend on the number of sides of the polygon. Participants may use the polygons that they have already constructed to study exterior angles for the ...
... Participants will now investigate the exterior angles of a polygon. It is often difficult for students to understand intuitively that this sum does not depend on the number of sides of the polygon. Participants may use the polygons that they have already constructed to study exterior angles for the ...
Regular polytope
In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces (for all 0 ≤ j ≤ n, where n is the dimension of the polytope) — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of dimension ≤ n. Regular polytopes are the generalized analog in any number of dimensions of regular polygons (for example, the square or the regular pentagon) and regular polyhedra (for example, the cube). The strong symmetry of the regular polytopes gives them an aesthetic quality that interests both non-mathematicians and mathematicians.Classically, a regular polytope in n dimensions may be defined as having regular facets [(n − 1)-faces] and regular vertex figures. These two conditions are sufficient to ensure that all faces are alike and all vertices are alike. Note, however, that this definition does not work for abstract polytopes.A regular polytope can be represented by a Schläfli symbol of the form {a, b, c, ...., y, z}, with regular facets as {a, b, c, ..., y}, and regular vertex figures as {b, c, ..., y, z}.