File
... 8.G ─ Understand congruence and similarity using physical models, transparencies, or geometry software. 2. Understand that a two-dimensional figure is congruent to another if the second can be obtained from the first by a sequence of rotations, reflections, and translations; given two congruent figu ...
... 8.G ─ Understand congruence and similarity using physical models, transparencies, or geometry software. 2. Understand that a two-dimensional figure is congruent to another if the second can be obtained from the first by a sequence of rotations, reflections, and translations; given two congruent figu ...
Foundations of Geometry
... description. We use these terms to describe other terms in geometry. 1) Point: a location. A point has neither shape nor size. When we name a point, we name it by a capital letter. Example: ...
... description. We use these terms to describe other terms in geometry. 1) Point: a location. A point has neither shape nor size. When we name a point, we name it by a capital letter. Example: ...
Laurel Pytko Discipline/Subject: Geometry
... Instructional Objective/Rationale – Students will be able to: 1. Define and identify parallel lines, skew lines, and parallel planes. 2. Define and identify transversal 3. Define and identify corresponding angles, alternate interior and exterior angles, and consecutive interior and exterior angles. ...
... Instructional Objective/Rationale – Students will be able to: 1. Define and identify parallel lines, skew lines, and parallel planes. 2. Define and identify transversal 3. Define and identify corresponding angles, alternate interior and exterior angles, and consecutive interior and exterior angles. ...
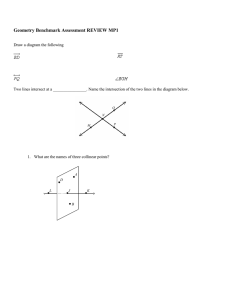
Math Homework Study Links pg.
... time extend the line on both ends and use arrowheads to show that it’s continuous. • Naming this Line • Line AB ...
... time extend the line on both ends and use arrowheads to show that it’s continuous. • Naming this Line • Line AB ...
Points, Lines, Planes, and Angles (chapter 1)
... G.2.2.2.3: Find the side lengths of a polygon with a given perimeter to maximize the area of the polygon. G.2.1.2.3: Use slope, distance and/or midpoint between 2 points on a coordinate plane to establish properties of a 2dimensional shape. ...
... G.2.2.2.3: Find the side lengths of a polygon with a given perimeter to maximize the area of the polygon. G.2.1.2.3: Use slope, distance and/or midpoint between 2 points on a coordinate plane to establish properties of a 2dimensional shape. ...
Curriculum Analysis
... about the angle sum of triangles, exterior angles of triangles, angles created when parallel lines are cut by a transversal, and angle-angle criterion for similarity of triangles. 8(8)(D) ...
... about the angle sum of triangles, exterior angles of triangles, angles created when parallel lines are cut by a transversal, and angle-angle criterion for similarity of triangles. 8(8)(D) ...
Syllabus for Accelerated Geometry
... analyze geometric figures using deductive reasoning, make conjectures and formulate hypotheses, draw conclusions and make connections with other mathematical concepts, and model situations geometrically as a problem solving strategy. Algebraic and geometric skills are integrated throughout the curri ...
... analyze geometric figures using deductive reasoning, make conjectures and formulate hypotheses, draw conclusions and make connections with other mathematical concepts, and model situations geometrically as a problem solving strategy. Algebraic and geometric skills are integrated throughout the curri ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.