Vocabulary Chapter 1A
... You should be familiar with these terms. There will be a multiple choice quiz in two days. You MUST be able to answer at least 80% of the questions correctly. Failure to do so will result in additional homework. ...
... You should be familiar with these terms. There will be a multiple choice quiz in two days. You MUST be able to answer at least 80% of the questions correctly. Failure to do so will result in additional homework. ...
Chapter 1 - Ithaca Public Schools
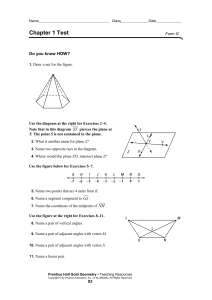
... A(n) ___________________________ is an accepted statement of fact. ___________________________ are coplanar lines that do not intersect. An ___________________________ is an angle whose measure is between 90 and 180. You can use ___________________________ when you make conclusions based on patterns ...
... A(n) ___________________________ is an accepted statement of fact. ___________________________ are coplanar lines that do not intersect. An ___________________________ is an angle whose measure is between 90 and 180. You can use ___________________________ when you make conclusions based on patterns ...
Hyperfunction Geometry
... An old (1980) program of mine is to develop hyperfunction geometry. It was motivated by work of Hawking on Euclidean Quantum Gravity and of Penrose on Twistor Quantization. Hawking considers complex 4-manifolds. To begin with, they admit Lorentzian sections. But he goes on to also need ones that don ...
... An old (1980) program of mine is to develop hyperfunction geometry. It was motivated by work of Hawking on Euclidean Quantum Gravity and of Penrose on Twistor Quantization. Hawking considers complex 4-manifolds. To begin with, they admit Lorentzian sections. But he goes on to also need ones that don ...
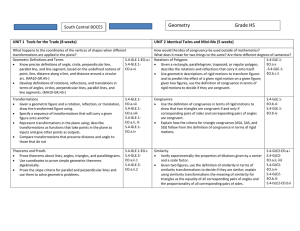
Geometry Scope and Sequence
... Verify experimentally the properties of dilations given by a center and a scale factor. Given two figures, use the definition of similarity in terms of similarity transformations to decide if they are similar; explain using similarity transformations the meaning of similarity for triangles as th ...
... Verify experimentally the properties of dilations given by a center and a scale factor. Given two figures, use the definition of similarity in terms of similarity transformations to decide if they are similar; explain using similarity transformations the meaning of similarity for triangles as th ...
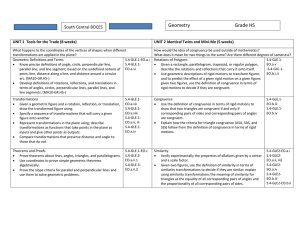
Geometry Scope and Sequence
... Verify experimentally the properties of dilations given by a center and a scale factor. Given two figures, use the definition of similarity in terms of similarity transformations to decide if they are similar; explain using similarity transformations the meaning of similarity for triangles as th ...
... Verify experimentally the properties of dilations given by a center and a scale factor. Given two figures, use the definition of similarity in terms of similarity transformations to decide if they are similar; explain using similarity transformations the meaning of similarity for triangles as th ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.