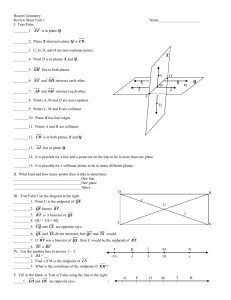
Handout 1 - Mathematics
... If A, B are two points on a line l, then the line segment AB is the part of the line between A and B (including A and B). The line segment AB is the intersection of ↑ AB and ↑ BA. Axiom 3. Suppose that O, A, B are points on a line. Then the rays ↑ OA, ↑ OB are the same if and only if AB does not con ...
... If A, B are two points on a line l, then the line segment AB is the part of the line between A and B (including A and B). The line segment AB is the intersection of ↑ AB and ↑ BA. Axiom 3. Suppose that O, A, B are points on a line. Then the rays ↑ OA, ↑ OB are the same if and only if AB does not con ...
Math 420 - Homework 3
... by arcs of great circles, and the area that is enclosed within. 1. When you consider the intersection of three distinct lines, how many sections have you now divided the sphere into? Note: From now on you can restrict your focus to just the smallest of the eight triangles. 2. In the Euclidean plane, ...
... by arcs of great circles, and the area that is enclosed within. 1. When you consider the intersection of three distinct lines, how many sections have you now divided the sphere into? Note: From now on you can restrict your focus to just the smallest of the eight triangles. 2. In the Euclidean plane, ...
Unit 7: Transformations in the Coordinate Plane
... At the end of Unit student’s should be able to say “I can…” describe and compare function transformations on a set of points as inputs to produce another set of points as outputs, including translations and horizontal or vertical stretching represent and compare rigid and size transformations of ...
... At the end of Unit student’s should be able to say “I can…” describe and compare function transformations on a set of points as inputs to produce another set of points as outputs, including translations and horizontal or vertical stretching represent and compare rigid and size transformations of ...
Teaching Notes - Centre for Innovation in Mathematics Teaching
... transformations and that the introduction of transformation geometry is just a fad – but there are strong reasons for the use of transformations in school geometry. One reason is that rotation, reflection, etc. can be introduced in a practical way and so should be more accessible to some pupils than ...
... transformations and that the introduction of transformation geometry is just a fad – but there are strong reasons for the use of transformations in school geometry. One reason is that rotation, reflection, etc. can be introduced in a practical way and so should be more accessible to some pupils than ...
2.5 Notes - APHS Mathematics
... _____________ and ___________ must intersect at C because if two line intersect, then ____________ _______________________________________________________. Point _____ is _______________ ________________ and point _____ is _________________. Points ____________________________ are __________________ ...
... _____________ and ___________ must intersect at C because if two line intersect, then ____________ _______________________________________________________. Point _____ is _______________ ________________ and point _____ is _________________. Points ____________________________ are __________________ ...
640109
... Prerequisite: [Math 026 or Math 107 or placement into Math 111] and [Permission of Department] Co-req.: none Special Notation: Primarily for those intending to teach in grades K-8 Course description: Math content course on geometry and measurement stressing depth of understanding needed for effectiv ...
... Prerequisite: [Math 026 or Math 107 or placement into Math 111] and [Permission of Department] Co-req.: none Special Notation: Primarily for those intending to teach in grades K-8 Course description: Math content course on geometry and measurement stressing depth of understanding needed for effectiv ...
Homework on Building Blocks of Geometry
... What geometric object is the intersection of two planes? ...
... What geometric object is the intersection of two planes? ...
Geometry Overview
... Use volume formulas for cylinders, pyramids, cones, and spheres to solve problems ...
... Use volume formulas for cylinders, pyramids, cones, and spheres to solve problems ...
Ch. 5/6 Test Review - Campbell County Schools
... Assume opposite of given Show contradiction Make conclusion ...
... Assume opposite of given Show contradiction Make conclusion ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.