Alternate Interior Angles
... Students will be able to: ◦ Identify relationships between figures in space Parallel and skew lines and planes ...
... Students will be able to: ◦ Identify relationships between figures in space Parallel and skew lines and planes ...
Honors Geometry Test 1 Topics I. Definitions and undefined terms A
... I. Definitions and undefined terms A. Know which terms are the three undefined terms B. Definitions in Topic 1 up through “angle” and “vertex of an angle” on page 6 (You might especially want to look at opposite rays, space, vertex, and midpoint) II. Notation and naming A. Notation for point, line, ...
... I. Definitions and undefined terms A. Know which terms are the three undefined terms B. Definitions in Topic 1 up through “angle” and “vertex of an angle” on page 6 (You might especially want to look at opposite rays, space, vertex, and midpoint) II. Notation and naming A. Notation for point, line, ...
MAT 3271: Selected solutions to problem sets 2 and 3 Chapter 1
... Proposition 2.3. For every line, there is at least one point not lying on it. Proof. Let l be a line. Consider the three non-collinear points given by Incidence Axiom 3. By definition, they cannot all lie on l. Thus there is a point not lying on l. Proposition 2.4. For every point, there is at least ...
... Proposition 2.3. For every line, there is at least one point not lying on it. Proof. Let l be a line. Consider the three non-collinear points given by Incidence Axiom 3. By definition, they cannot all lie on l. Thus there is a point not lying on l. Proposition 2.4. For every point, there is at least ...
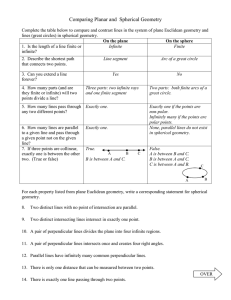
Comparing Planar and Spherical Geometry
... 11. A pair of perpendicular lines intersects once and creates four right angles. 12. Parallel lines have infinitely many common perpendicular lines. 13. There is only one distance that can be measured between two points. OVER 14. There is exactly one line passing through two points. ...
... 11. A pair of perpendicular lines intersects once and creates four right angles. 12. Parallel lines have infinitely many common perpendicular lines. 13. There is only one distance that can be measured between two points. OVER 14. There is exactly one line passing through two points. ...
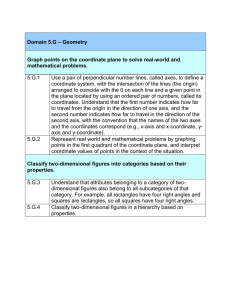
Geometry Standards
... Use a pair of perpendicular number lines, called axes, to define a coordinate system, with the intersection of the lines (the origin) arranged to coincide with the 0 on each line and a given point in the plane located by using an ordered pair of numbers, called its coordinates. Understand that the f ...
... Use a pair of perpendicular number lines, called axes, to define a coordinate system, with the intersection of the lines (the origin) arranged to coincide with the 0 on each line and a given point in the plane located by using an ordered pair of numbers, called its coordinates. Understand that the f ...
Chapter 1
... 2. To help develop facility with logical thinking. (This includes, in particular, the distinction between reasoning from abstract axioms containing undefined terms and reasoning from facts about things we already know something about.) 3. To prepare future teachers of high-school geometry to approac ...
... 2. To help develop facility with logical thinking. (This includes, in particular, the distinction between reasoning from abstract axioms containing undefined terms and reasoning from facts about things we already know something about.) 3. To prepare future teachers of high-school geometry to approac ...
Alternate Interior Angles
... If there is a line and a point not on the line, then there is exactly one line through the point ║ to the given line. P ...
... If there is a line and a point not on the line, then there is exactly one line through the point ║ to the given line. P ...
LIST # 2: Geometry Vocabulary Words:
... angle and direction about a fixed point, called the center of rotation 15. Scale Factor: the ratios of the lengths of two corresponding sides of two similar polygons or two similar solids 16. Dilation: a transformation determined by a center point P and scale factor 17. Surface Area: the sum of the ...
... angle and direction about a fixed point, called the center of rotation 15. Scale Factor: the ratios of the lengths of two corresponding sides of two similar polygons or two similar solids 16. Dilation: a transformation determined by a center point P and scale factor 17. Surface Area: the sum of the ...
Geometry - Crossword Labs
... 17. Opposite angles formed when two lines intersect. 18. The point halfway between the endpoints of a line segment. ...
... 17. Opposite angles formed when two lines intersect. 18. The point halfway between the endpoints of a line segment. ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.