Vocabulary Chapter 1B
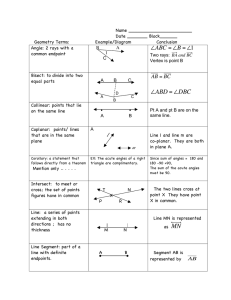
... Coplanar points- points that lie in the same plane Noncoplanar points- points that do not lie in the same plane Opposite rays-two rays that have a common endpoint and form a line Postulate- statement that is accepted as true without proof Coordinate- a number on a ruler that corresponds to a point D ...
... Coplanar points- points that lie in the same plane Noncoplanar points- points that do not lie in the same plane Opposite rays-two rays that have a common endpoint and form a line Postulate- statement that is accepted as true without proof Coordinate- a number on a ruler that corresponds to a point D ...
A replacement for a variable that results in a true sentence
... Directions: Cut out the definitions. Find the vocabulary term that matches each definition given. ...
... Directions: Cut out the definitions. Find the vocabulary term that matches each definition given. ...
File
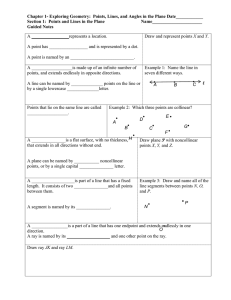
... The box represents a plane called O. The walls the floor and the ceiling all represent planes. ...
... The box represents a plane called O. The walls the floor and the ceiling all represent planes. ...
A represents a location
... A point has _________________ and is represented by a dot. A point is named by an ____________________________. A __________________is made up of an infinite number of points, and extends endlessly in opposite directions. ...
... A point has _________________ and is represented by a dot. A point is named by an ____________________________. A __________________is made up of an infinite number of points, and extends endlessly in opposite directions. ...
1300Y Geometry and Topology, Assignment 1 Exercise 1. Let Γ be a
... b) Show that M naturally inherits the structure of a smooth manifold. c) Let M̃ = S n and Let Γ = Z/2Z act via h · x = −x, where h is the generator of Γ. Show that the hypotheses above are satisfied, and identify the resulting quotient manifold. d) Let M̃ = Cn − {0} and let the generator of Γ = Z ac ...
... b) Show that M naturally inherits the structure of a smooth manifold. c) Let M̃ = S n and Let Γ = Z/2Z act via h · x = −x, where h is the generator of Γ. Show that the hypotheses above are satisfied, and identify the resulting quotient manifold. d) Let M̃ = Cn − {0} and let the generator of Γ = Z ac ...
Read 1.4, 2.6 Incidence Axiom 1. For each two distinct points there
... points P and Q of a line, the coordinate system can be chosen in such a way that the coordinates of P and Q are 0 and 0. 5. (a) Every plane contains at least 3 noncollinear points. (b) Space contains at least 4 noncoplanar points. 6. If 2 points lie in a plane, then the line containing these point ...
... points P and Q of a line, the coordinate system can be chosen in such a way that the coordinates of P and Q are 0 and 0. 5. (a) Every plane contains at least 3 noncollinear points. (b) Space contains at least 4 noncoplanar points. 6. If 2 points lie in a plane, then the line containing these point ...
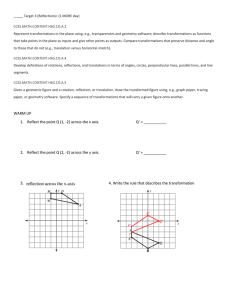
_____ Target 3 (Reflections): (1 MORE day) CCSS.MATH
... that take points in the plane as inputs and give other points as outputs. Compare transformations that preserve distance and angle to those that do not (e.g., translation versus horizontal stretch). CCSS.MATH.CONTENT.HSG.CO.A.4 Develop definitions of rotations, reflections, and translations in terms ...
... that take points in the plane as inputs and give other points as outputs. Compare transformations that preserve distance and angle to those that do not (e.g., translation versus horizontal stretch). CCSS.MATH.CONTENT.HSG.CO.A.4 Develop definitions of rotations, reflections, and translations in terms ...
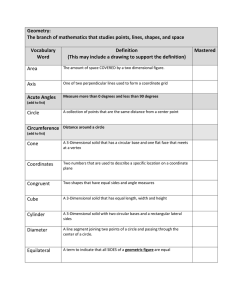
This may include a drawing to support the definition
... (This may include a drawing to support the definition) ...
... (This may include a drawing to support the definition) ...
Your 1st Geometry Test
... • A triangle that has two congruent sides. ISOSCELES • Angles that have the same measure. CONGRUENT • A triangle that has no congruent sides. SCALENE • Two lines that intersect to form right angles. PERPENDICULAR • A set of three or more points all of which lie on the same straight line. COLLINEAR ...
... • A triangle that has two congruent sides. ISOSCELES • Angles that have the same measure. CONGRUENT • A triangle that has no congruent sides. SCALENE • Two lines that intersect to form right angles. PERPENDICULAR • A set of three or more points all of which lie on the same straight line. COLLINEAR ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.