Lines and planes
... Two planes n1 · (r − a1 ) = 0 and n1 · (r − a2 ) = 0 are parallel if and only if their normal vectors n1 and n2 are parallel or opposite. If two planes are parallel then they either intersect everywhere (they’re the same plane) or they don’t intersect at all. If two planes are not parallel then they ...
... Two planes n1 · (r − a1 ) = 0 and n1 · (r − a2 ) = 0 are parallel if and only if their normal vectors n1 and n2 are parallel or opposite. If two planes are parallel then they either intersect everywhere (they’re the same plane) or they don’t intersect at all. If two planes are not parallel then they ...
The geometry of the universe - University of Maryland Astronomy
... North Pole and the others at the equator, 90 degrees of longitude apart. It is easy to see that this triangle has three right angles, for a total of 270 degrees! How about a circle? Suppose we take the equator. Its circumference is 2πR, where R is the radius of the sphere. You might be tempted to s ...
... North Pole and the others at the equator, 90 degrees of longitude apart. It is easy to see that this triangle has three right angles, for a total of 270 degrees! How about a circle? Suppose we take the equator. Its circumference is 2πR, where R is the radius of the sphere. You might be tempted to s ...
Algebraic Geometry I
... Write up solutions to three of the problems (write as legibly and clearly as you can, preferably in LaTeX). 1. (Intersection Multiplicities.) Let C = V (f ) and D = V (g) be two distinct curves in A2 . Recall that the multiplicity of intersection mp (C, D) of C and D at p is defined as the dimension ...
... Write up solutions to three of the problems (write as legibly and clearly as you can, preferably in LaTeX). 1. (Intersection Multiplicities.) Let C = V (f ) and D = V (g) be two distinct curves in A2 . Recall that the multiplicity of intersection mp (C, D) of C and D at p is defined as the dimension ...
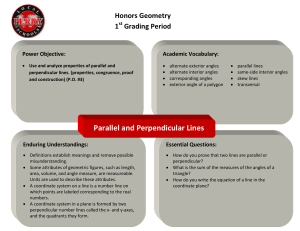
Geometry Course Objectives Student Study Guide
... • Identify vertical, adjacent, complementary, and supplementary angle pairs and use them to solve problems (e.g., solve equations, use in proofs) • Identify corresponding, same-side interior, same-side exterior, alternate interior, and alternate exterior angle pairs formed by a pair of parallel line ...
... • Identify vertical, adjacent, complementary, and supplementary angle pairs and use them to solve problems (e.g., solve equations, use in proofs) • Identify corresponding, same-side interior, same-side exterior, alternate interior, and alternate exterior angle pairs formed by a pair of parallel line ...
Things start to get complicated when the single point separates into
... Next is four circles (image three0, with the "Eye of Life," at its center. Now we aren't just looking at God, God is looking back! In ancient Egypt this is known as the Eye of Horus, and in the bible as the Eye of God or Providence. The Buddha is also known as the Eye of the World. This one might b ...
... Next is four circles (image three0, with the "Eye of Life," at its center. Now we aren't just looking at God, God is looking back! In ancient Egypt this is known as the Eye of Horus, and in the bible as the Eye of God or Providence. The Buddha is also known as the Eye of the World. This one might b ...
Lesson Plan 1
... Geometry the sum of angles of a triangle is 180. 3) States to the students that in Hyperbolic Geometry the sum of the angles of a triangle is less than 180. Show some examples. 4) States to the students that in Hyperbolic Geometry, all the axioms for neutral geometry hold, but the parallel postulate ...
... Geometry the sum of angles of a triangle is 180. 3) States to the students that in Hyperbolic Geometry the sum of the angles of a triangle is less than 180. Show some examples. 4) States to the students that in Hyperbolic Geometry, all the axioms for neutral geometry hold, but the parallel postulate ...
EUCLIDEAN AND NON-EUCLIDEAN GEOMETRY
... Let us look back in history. Since the Greeks, geometry has had a dual aspect. It is claimed to be an accurate description of the space in which we live and it is also an intellectual discipline, a deductive structure. These two aspects are now viewed as separate, but this was not always the case. T ...
... Let us look back in history. Since the Greeks, geometry has had a dual aspect. It is claimed to be an accurate description of the space in which we live and it is also an intellectual discipline, a deductive structure. These two aspects are now viewed as separate, but this was not always the case. T ...
lecture 25
... are equal. (Here len(s1 ) refers to the length of s1 , and so on...) We then talked about Descartes, who invented a cunning technique for turning problems in geometry into problems in algebra: the Cartesian plane. Each point in the plane is labelled with a pair of (real) numbers—the x coordinate, an ...
... are equal. (Here len(s1 ) refers to the length of s1 , and so on...) We then talked about Descartes, who invented a cunning technique for turning problems in geometry into problems in algebra: the Cartesian plane. Each point in the plane is labelled with a pair of (real) numbers—the x coordinate, an ...
Content Area
... Priority Standards HSG-CO.A.5 Given a geometric figure and a rotation, reflection, or translation, draw the transformed figure using, e.g., graph paper, tracing paper, or geometry software. Specify a sequence of transformations that will carry a given figure onto another. HSG-C0.B.6 Use geometric de ...
... Priority Standards HSG-CO.A.5 Given a geometric figure and a rotation, reflection, or translation, draw the transformed figure using, e.g., graph paper, tracing paper, or geometry software. Specify a sequence of transformations that will carry a given figure onto another. HSG-C0.B.6 Use geometric de ...
Glenbard District 87
... the formula for the area of a sector. G.GPE.1 Derive the equation of a circle of given center and radius using the Pythagorean Theorem; complete the square to find the center and radius of a circle given by an equation. G.GPE.4 Use coordinates to prove simple geometric theorems algebraically. For ex ...
... the formula for the area of a sector. G.GPE.1 Derive the equation of a circle of given center and radius using the Pythagorean Theorem; complete the square to find the center and radius of a circle given by an equation. G.GPE.4 Use coordinates to prove simple geometric theorems algebraically. For ex ...
Definitions and Notations of SMSG and Neutral Geometry
... (m) A bisector of an angle ∠BAC is a ray AD that is contained in ∠BAC and such that m∠BAD = m∠DAC = 12 m∠BAC. (n) Two lines l1 , l2 are said to be perpendicular if they intersect at a point A such that for any point B on l1 and any point C on l2 such that B 6= A and C 6= A the angle ∠BAC is right. ( ...
... (m) A bisector of an angle ∠BAC is a ray AD that is contained in ∠BAC and such that m∠BAD = m∠DAC = 12 m∠BAC. (n) Two lines l1 , l2 are said to be perpendicular if they intersect at a point A such that for any point B on l1 and any point C on l2 such that B 6= A and C 6= A the angle ∠BAC is right. ( ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.