On feebly compact shift-continuous topologies on the semilattice
... Theorem 2. Every quasiregular d-feebly compact space is feebly compact. Proof. Suppose to the contrary that there exists a quasiregular d-feebly compact space X which is not feebly compact. Then there exists an infinite locally finite family U0 of non-empty open subsets of X. By induction we shall c ...
... Theorem 2. Every quasiregular d-feebly compact space is feebly compact. Proof. Suppose to the contrary that there exists a quasiregular d-feebly compact space X which is not feebly compact. Then there exists an infinite locally finite family U0 of non-empty open subsets of X. By induction we shall c ...
Generically there is but one self homeomorphism of the Cantor set
... A topological group G is called Rohlin if there is an element g ∈ G whose conjugacy class is dense in G. In [GW] it was shown that the Polish group H(X) of homeomorphisms of the Cantor set X is Rohlin. The same result was independently obtained in [AHK] and the authors there posed the question wheth ...
... A topological group G is called Rohlin if there is an element g ∈ G whose conjugacy class is dense in G. In [GW] it was shown that the Polish group H(X) of homeomorphisms of the Cantor set X is Rohlin. The same result was independently obtained in [AHK] and the authors there posed the question wheth ...
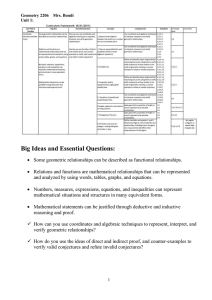
Objective(s) - Shelby County Schools
... The TN State Standards are located in the left column. Each content standard is identified as the following: Major Work, Supporting Content or Additional Content.; a key can be found at the bottom of the map. The major work of the grade should comprise 65-85% of your instructional time. Supporting C ...
... The TN State Standards are located in the left column. Each content standard is identified as the following: Major Work, Supporting Content or Additional Content.; a key can be found at the bottom of the map. The major work of the grade should comprise 65-85% of your instructional time. Supporting C ...
Name - North Penn School District
... Segment bisector – a point, line, or ray that intersects a segment at its __________________ Label CD and midpoint M to show that MN is the segment bisector of CD . ...
... Segment bisector – a point, line, or ray that intersects a segment at its __________________ Label CD and midpoint M to show that MN is the segment bisector of CD . ...
minimalrevised.pdf
... Note that if x ∈ X is a beat point, there exists y ∈ X, y 6= x, with the following property: Given any z ∈ X, if z is comparable with x, then z is also comparable with y. Moreover, it is not difficult to prove the following characterization of minimal finite spaces. Proposition 2.3. Let X be a finit ...
... Note that if x ∈ X is a beat point, there exists y ∈ X, y 6= x, with the following property: Given any z ∈ X, if z is comparable with x, then z is also comparable with y. Moreover, it is not difficult to prove the following characterization of minimal finite spaces. Proposition 2.3. Let X be a finit ...
RCHS Rev. 06/2011 Geometry A Unit One Congruence Length of
... dilations given by a center and a scale factor. b. The dilation of a line segment is longer or shorter in the ratio given by the scale factor. G.SRT.2 Given two figures, use the definition of similarity in terms of similarity transformations to decide if they are similar; explain using similarity tr ...
... dilations given by a center and a scale factor. b. The dilation of a line segment is longer or shorter in the ratio given by the scale factor. G.SRT.2 Given two figures, use the definition of similarity in terms of similarity transformations to decide if they are similar; explain using similarity tr ...
4-6
... Two congruent angle pairs are give, but the included sides are not given as congruent. Therefore ASA cannot be used to prove the triangles congruent. Holt McDougal Geometry ...
... Two congruent angle pairs are give, but the included sides are not given as congruent. Therefore ASA cannot be used to prove the triangles congruent. Holt McDougal Geometry ...
A NOTE ON MINIMAL DYNAMICAL SYSTEMS 1. Introduction Let G
... disconnected, that is, they are Stone spaces of complete Boolean algebras. This is where Cohen algebras enter the picture. A complete Boolean algebra is Cohen if it is the completion of a free Boolean algebra. Balcar and Blaszczyk [1] showed that extremely disconnected phase spaces of minimal system ...
... disconnected, that is, they are Stone spaces of complete Boolean algebras. This is where Cohen algebras enter the picture. A complete Boolean algebra is Cohen if it is the completion of a free Boolean algebra. Balcar and Blaszczyk [1] showed that extremely disconnected phase spaces of minimal system ...
Old and New Results in the Foundations of Elementary Plane
... some of his own axioms from the others, he presented unusual models to show certain statements unprovable from others, and in subsequent editions he explored in his appendices many other interesting topics, including his foundation for plane hyperbolic geometry without bringing in real numbers. Thus ...
... some of his own axioms from the others, he presented unusual models to show certain statements unprovable from others, and in subsequent editions he explored in his appendices many other interesting topics, including his foundation for plane hyperbolic geometry without bringing in real numbers. Thus ...