FULL TEXT
... the bitopological space (R, U, L), where R is the set of real numbers and U and L are the upper and lower topologies on R, namely U = {∅, R, (a, ∞) : a ∈ R} and L = {∅, R, (−∞, a) : a ∈ R}. Then (R, U, L) is pairwise normal, and satisfies the weak version of each of the other separation properties, ...
... the bitopological space (R, U, L), where R is the set of real numbers and U and L are the upper and lower topologies on R, namely U = {∅, R, (a, ∞) : a ∈ R} and L = {∅, R, (−∞, a) : a ∈ R}. Then (R, U, L) is pairwise normal, and satisfies the weak version of each of the other separation properties, ...
File
... A reflection across the xaxis and translation one unit right and one unit down B reflection across the xaxis and translation one unit left and one unit up C rotation of 180° around the origin and translation one unit right and one unit down D rotation of 90° around the origin and translation ...
... A reflection across the xaxis and translation one unit right and one unit down B reflection across the xaxis and translation one unit left and one unit up C rotation of 180° around the origin and translation one unit right and one unit down D rotation of 90° around the origin and translation ...
SOLUTIONS TO EXERCISES FOR MATHEMATICS 205A — Part 5
... Suppose now that X is countably infinite. The same formula holds, but the product of the D i ’s is not necessarily countable. To adjust Q for this, pick some point δ j ∈ Dj for each j and consider the set E of all points (a0 , a1 , · · · ) in j Dj such that aj = δj for all but at most finitely many ...
... Suppose now that X is countably infinite. The same formula holds, but the product of the D i ’s is not necessarily countable. To adjust Q for this, pick some point δ j ∈ Dj for each j and consider the set E of all points (a0 , a1 , · · · ) in j Dj such that aj = δj for all but at most finitely many ...
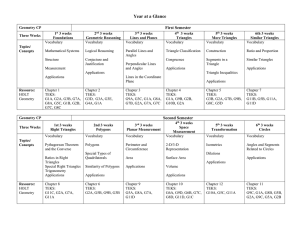
Geometry CP Scope and Sequenc
... First Semester, 2nd 3 Weeks Logical Reasoning and Conjecture (Approximate Time: 3 weeks) ELOs TEKS Topics (not in sequential order) The student will: -make conjectures based on inductive reasoning. -analyze statements in if-then form (conditional statements). -write the converse, inverse, and contr ...
... First Semester, 2nd 3 Weeks Logical Reasoning and Conjecture (Approximate Time: 3 weeks) ELOs TEKS Topics (not in sequential order) The student will: -make conjectures based on inductive reasoning. -analyze statements in if-then form (conditional statements). -write the converse, inverse, and contr ...
The Open Limit Point Compactness
... point compactness.The section one included the fundamental topological concepts such as, topological property, hereditary property, and limit point compactness. In section two, we gave the main results of this paper which are a new topological concepts, an open limit point compactness. 1. Fundamenta ...
... point compactness.The section one included the fundamental topological concepts such as, topological property, hereditary property, and limit point compactness. In section two, we gave the main results of this paper which are a new topological concepts, an open limit point compactness. 1. Fundamenta ...
Gr04_Ch_10 - Etiwanda E
... California Standards Key Concept: Turns and Angles Key Concept: Types of Angles ...
... California Standards Key Concept: Turns and Angles Key Concept: Types of Angles ...