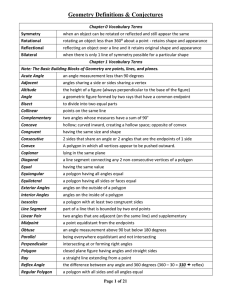
English
... situation arises with the homology groups –introduced by H. Poincaré in 1895− since, for a diversity of topological spaces, the algebraic structure of their associated homology groups can be calculated. There are not many algorithms to compute absolute (or relative) homotopy groups of a topological ...
... situation arises with the homology groups –introduced by H. Poincaré in 1895− since, for a diversity of topological spaces, the algebraic structure of their associated homology groups can be calculated. There are not many algorithms to compute absolute (or relative) homotopy groups of a topological ...
n - AGMath.com
... Induction is very important in geometry. Often, a pattern in geometry is recognized before it is fully understood. Today we will use inductive reasoning to discover the sum of the measures of interior angles in a pentagon. With a partner: Use a straight-edge to draw an irregular convex pentagon. Tra ...
... Induction is very important in geometry. Often, a pattern in geometry is recognized before it is fully understood. Today we will use inductive reasoning to discover the sum of the measures of interior angles in a pentagon. With a partner: Use a straight-edge to draw an irregular convex pentagon. Tra ...
6.3 Parallelogram theorems
... Both pairs of opposite sides have the same slope so and by definition, KLMN is a parallelogram. Holt McDougal Geometry ...
... Both pairs of opposite sides have the same slope so and by definition, KLMN is a parallelogram. Holt McDougal Geometry ...


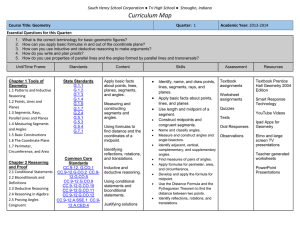

















![arXiv:0903.2024v3 [math.AG] 9 Jul 2009](http://s1.studyres.com/store/data/016334314_1-5f7029642e57766ba62e6f9f2c64e435-300x300.png)