1-3
... with a common endpoint called the vertex (plural: vertices). You can name an angle several ways: by its vertex, by a point on each ray and the vertex, or by a number. ...
... with a common endpoint called the vertex (plural: vertices). You can name an angle several ways: by its vertex, by a point on each ray and the vertex, or by a number. ...
Geometry - Piscataway High School
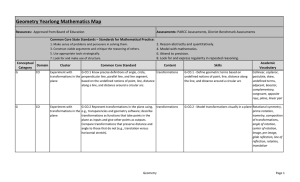
... Identify vocabulary related to reasoning (inductive reasoning, deductive reasoning, conjecture, theorem, conditional statements and counterexamples) Discuss postulates about Lines and Planes Complete simple proofs and algebraic proofs using properties and postulates to justify statements (refer to e ...
... Identify vocabulary related to reasoning (inductive reasoning, deductive reasoning, conjecture, theorem, conditional statements and counterexamples) Discuss postulates about Lines and Planes Complete simple proofs and algebraic proofs using properties and postulates to justify statements (refer to e ...
An Introduction to Non-Euclidean Geometry
... 2. If equals are added to equals, then the wholes are equal. 3. If equals are subtracted from equals, then the remainders are equal. 4. Things which coincide with one another equal one another. 5. The whole is greater than the part. ...
... 2. If equals are added to equals, then the wholes are equal. 3. If equals are subtracted from equals, then the remainders are equal. 4. Things which coincide with one another equal one another. 5. The whole is greater than the part. ...
Geometry-13-17 January 2013 -polygon - Shope-Math
... Write in your Notes 1)EXPLAIN in writing THINK-PAIR- SHARE WHAT are THREE DIFFERENT METHODS that could be used to find the interior angle sum of any polygon? 2) USE at least 2 different methods to find the missing interior angle sum of a hexagon. Clearly show your thinking. ...
... Write in your Notes 1)EXPLAIN in writing THINK-PAIR- SHARE WHAT are THREE DIFFERENT METHODS that could be used to find the interior angle sum of any polygon? 2) USE at least 2 different methods to find the missing interior angle sum of a hexagon. Clearly show your thinking. ...
normed linear spaces of continuous functions
... The first of these is the general question as to relations between the topological properties of X and the properties (algebraic, topological, metric) of B(X) and its linear subspaces. The impetus to the study of this question has been given by various results which show that, under certain natural ...
... The first of these is the general question as to relations between the topological properties of X and the properties (algebraic, topological, metric) of B(X) and its linear subspaces. The impetus to the study of this question has been given by various results which show that, under certain natural ...
REPRESENTATION THEOREMS FOR CONNECTED COMPACT
... in any topological space. Stone in [11] gives a representation theorem for such algebras. This line of research was taken up again by Priestley in [9], where she provided what is now known as Priestley duality. It associates to distributive lattices a compact Hausdorff space endowed with an order. T ...
... in any topological space. Stone in [11] gives a representation theorem for such algebras. This line of research was taken up again by Priestley in [9], where she provided what is now known as Priestley duality. It associates to distributive lattices a compact Hausdorff space endowed with an order. T ...