Euclid`s Fifth Postulate - Indian Academy of Sciences
... write an all-time bestseller, a classic book read and scrutinized for the last twenty three centuries.” The book is called 'The Elements’ and consists of 13 books all devoted to various aspects of geometry and number theory. Of these, the most quoted is the one on the fundamentals of geometry Book I ...
... write an all-time bestseller, a classic book read and scrutinized for the last twenty three centuries.” The book is called 'The Elements’ and consists of 13 books all devoted to various aspects of geometry and number theory. Of these, the most quoted is the one on the fundamentals of geometry Book I ...
PACING_GUIDE_GEOMETRY_
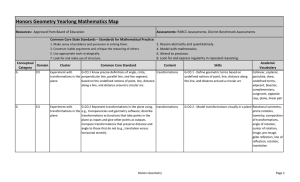
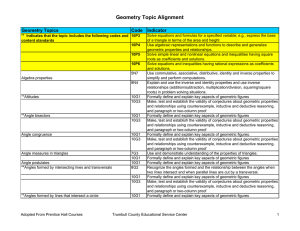
... Geometry is designed for students who have successfully completed the standards for Algebra I. All students are expected to achieve the Geometry standards. The course includes, but is not limited to, properties of geometric figures, trigonometric relationships, and reasoning to justify conclusions. ...
... Geometry is designed for students who have successfully completed the standards for Algebra I. All students are expected to achieve the Geometry standards. The course includes, but is not limited to, properties of geometric figures, trigonometric relationships, and reasoning to justify conclusions. ...
BOREL SETS, WELL-ORDERINGS OF R AND THE CONTINUUM
... (X, T ), where T is the topology with open basis B(x, r) = {y ∈ X | d(x, y) < r} x ∈ X, r > 0. In this case, we say that the metric d is compatible with the topology T and we also say that the topology T is metrizable. Definition 2.2. A topological space X is said to be Hausdorff iff for all x 6= y ...
... (X, T ), where T is the topology with open basis B(x, r) = {y ∈ X | d(x, y) < r} x ∈ X, r > 0. In this case, we say that the metric d is compatible with the topology T and we also say that the topology T is metrizable. Definition 2.2. A topological space X is said to be Hausdorff iff for all x 6= y ...
Introduction to Hyperbolic Geometry
... Introduction to Hyperbolic Geometry The major difference that we have stressed throughout the semester is that there is one small difference in the parallel postulate between Euclidean and hyperbolic geometry. We have been working with eight axioms. Let’s recall the first seven and then add our new ...
... Introduction to Hyperbolic Geometry The major difference that we have stressed throughout the semester is that there is one small difference in the parallel postulate between Euclidean and hyperbolic geometry. We have been working with eight axioms. Let’s recall the first seven and then add our new ...
On πp- Compact spaces and πp
... *Asst. Professor, Dept. of Mathematics, Sree Narayana Guru College, Coimbatore- 105, India. ** Asst. Professor, Dept. of Mathematics, L.R.G. Govt. Arts College for Women, Tirupur-4, India. Email:* [email protected], ** [email protected] ...
... *Asst. Professor, Dept. of Mathematics, Sree Narayana Guru College, Coimbatore- 105, India. ** Asst. Professor, Dept. of Mathematics, L.R.G. Govt. Arts College for Women, Tirupur-4, India. Email:* [email protected], ** [email protected] ...
Inner separation structures for topological spaces
... axioms on topological spaces. Our constructions generate a method to refine separation properties when passing to the quotient space and our results may be useful in the study of algebraic topological structures, such as topological groups and topological vector spaces. M.S.C. 2000: 54D10, 54D15, 54 ...
... axioms on topological spaces. Our constructions generate a method to refine separation properties when passing to the quotient space and our results may be useful in the study of algebraic topological structures, such as topological groups and topological vector spaces. M.S.C. 2000: 54D10, 54D15, 54 ...
Axiomatic Geometry: Euclid and Beyond
... To produce a finite straight-line continuously in a straight-line. To draw a circle with any center and radius. All right-angles are equal to one another. Parallel axiom: If a straight line ` cuts two other straight lines m and n such that the sum of the internal angles on one side is less than two ...
... To produce a finite straight-line continuously in a straight-line. To draw a circle with any center and radius. All right-angles are equal to one another. Parallel axiom: If a straight line ` cuts two other straight lines m and n such that the sum of the internal angles on one side is less than two ...