Comparing Planar and Spherical Geometry
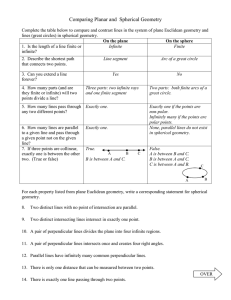
... For each property listed from plane Euclidean geometry, write a corresponding statement for spherical geometry. ...
... For each property listed from plane Euclidean geometry, write a corresponding statement for spherical geometry. ...
Chapter 1 Test Review Period ______ 1. Two nonadjacent angles f
... 2. An angle whose measure is greater than 0° and less than 90° is a(n): 3. A segment, ray, line or plane that divides a segment into two congruent segments is a: 4. A figure formed by two rays with a common endpoint is a(n): 5. Points that lie on the same line are: 6. Points that lie on the same pla ...
... 2. An angle whose measure is greater than 0° and less than 90° is a(n): 3. A segment, ray, line or plane that divides a segment into two congruent segments is a: 4. A figure formed by two rays with a common endpoint is a(n): 5. Points that lie on the same line are: 6. Points that lie on the same pla ...
guided notes day one of geo -
... Classifying Triangles + Triangle Sum Theorem Triangles can be classified two ways—by their angles and by their sides. If classifying by angles: ...
... Classifying Triangles + Triangle Sum Theorem Triangles can be classified two ways—by their angles and by their sides. If classifying by angles: ...