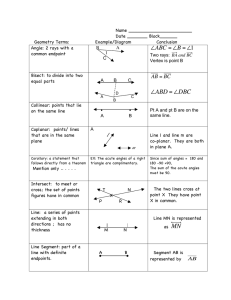
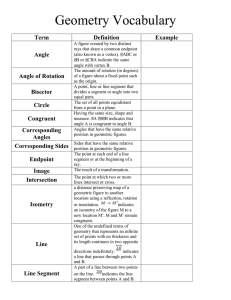
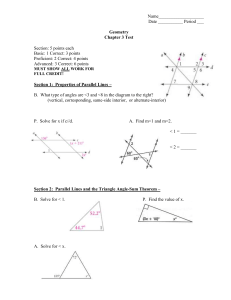
Triangle Inequality – examples…
... Finding the range of the third side: Since the third side cannot be larger than the other two added together, we find the maximum value by adding the two sides. Since the third side and the smallest side cannot be larger than the other side, we find the minimum value by subtracting the two sides. E ...
... Finding the range of the third side: Since the third side cannot be larger than the other two added together, we find the maximum value by adding the two sides. Since the third side and the smallest side cannot be larger than the other side, we find the minimum value by subtracting the two sides. E ...
Reteach 4.3
... one side of the triangle and the extension of an adjacent side. ∠1 and ∠2 are the remote interior angles of ∠4 because they are not adjacent to ∠4. Exterior Angle Theorem ...
... one side of the triangle and the extension of an adjacent side. ∠1 and ∠2 are the remote interior angles of ∠4 because they are not adjacent to ∠4. Exterior Angle Theorem ...