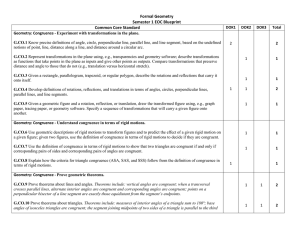
Formal Geometry Semester 1 EOC Blueprint Common Core
... Geometry: Congruence - Prove geometric theorems. G.CO.9 Prove theorems about lines and angles. Theorems include: vertical angles are congruent; when a transversal crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent; points on a perpendicular bisecto ...
... Geometry: Congruence - Prove geometric theorems. G.CO.9 Prove theorems about lines and angles. Theorems include: vertical angles are congruent; when a transversal crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent; points on a perpendicular bisecto ...
File
... The ratio of a circle’s circumference to its diameter is the same for all circles. This ratio is represented by the Greek letter (pi). The value of is irrational. Pi is often approximated as 3.14 or ...
... The ratio of a circle’s circumference to its diameter is the same for all circles. This ratio is represented by the Greek letter (pi). The value of is irrational. Pi is often approximated as 3.14 or ...
part-2-of-2-north-country-ccssm-hs-march-inservice
... Dilation is a Non-Rigid Transformation that preserves angle, but involves a scaling factor that affects the distance, which results in images that are similar to the original shape. G-SRT Cluster Headings dealing with Similarity: • Understand Similarity in terms of similarity transformations • Prove ...
... Dilation is a Non-Rigid Transformation that preserves angle, but involves a scaling factor that affects the distance, which results in images that are similar to the original shape. G-SRT Cluster Headings dealing with Similarity: • Understand Similarity in terms of similarity transformations • Prove ...
The discovery of non-Euclidean geometries
... named H.S.M. Coxeter (1907-2003) – University of Toronto – who was interested in the art for its mathematical connections Escher claimed not to be able to follow any of the mathematics that Coxeter used to try to explain things that Escher asked him about But a diagram Coxeter sent to Escher did ...
... named H.S.M. Coxeter (1907-2003) – University of Toronto – who was interested in the art for its mathematical connections Escher claimed not to be able to follow any of the mathematics that Coxeter used to try to explain things that Escher asked him about But a diagram Coxeter sent to Escher did ...
Name Unit 1 Overview/Review Projected Test Date: September 5
... On a certain farm, individual crops are laid out in rectangles that are 60 feet north and south, and 40 feet east and west. How far would you have to walk to get from the shed (S) to the well (W) if you did not step on any crops? How far would it be if you walked diagonally across the crops? ...
... On a certain farm, individual crops are laid out in rectangles that are 60 feet north and south, and 40 feet east and west. How far would you have to walk to get from the shed (S) to the well (W) if you did not step on any crops? How far would it be if you walked diagonally across the crops? ...
Chapter 3 Parallel and Perpendicular Lines
... We know them they are easy A line can be drawn between 2 points Any line segment can be a line Circles exist with a given radius All right angles are congruent Parallel lines exist ...
... We know them they are easy A line can be drawn between 2 points Any line segment can be a line Circles exist with a given radius All right angles are congruent Parallel lines exist ...
Euclidean Geometry and History of Non
... line L and a point p outside L, there exists no line parallel to L passing through p. Elliptic geometry, like hyperbolic geometry, violates Euclid's parallel postulate, which asserts that there is exactly one line parallel to L passing through p. In elliptic geometry, there are no parallel lines at ...
... line L and a point p outside L, there exists no line parallel to L passing through p. Elliptic geometry, like hyperbolic geometry, violates Euclid's parallel postulate, which asserts that there is exactly one line parallel to L passing through p. In elliptic geometry, there are no parallel lines at ...
Spherical Geometry Homework
... and this is the one in the undefined terms) and tangent planes in surrounding 3D space. We will use the planes in 3D space that are tangent to the surface of the sphere to measure angles, but these are not the undefined term “plane”; these are Euclidean planes in the embedding space. space: We don’t ...
... and this is the one in the undefined terms) and tangent planes in surrounding 3D space. We will use the planes in 3D space that are tangent to the surface of the sphere to measure angles, but these are not the undefined term “plane”; these are Euclidean planes in the embedding space. space: We don’t ...
Lines that intersect Circles
... Diameter: -a chord that contains the center -connects two points on the circle and passes through the ...
... Diameter: -a chord that contains the center -connects two points on the circle and passes through the ...
Was there a Revolution in Geometry in the Nineteenth Century?
... others of Euclid’s axioms are reinterpreted, a consistent geometry can be based upon the previously rejected hypothesis of the obtuse angle. The resulting geometry applies, for example, on the surface of a sphere. In this system the area of a triangle is proportional to its angular excess. Secondly, ...
... others of Euclid’s axioms are reinterpreted, a consistent geometry can be based upon the previously rejected hypothesis of the obtuse angle. The resulting geometry applies, for example, on the surface of a sphere. In this system the area of a triangle is proportional to its angular excess. Secondly, ...