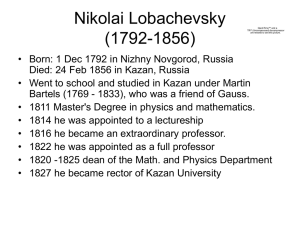Nikolai Lobachevsky (1792-1856)
... Finally he shows that the dichotomy extends to parallels. • In Euclidean geometry there is exactly one parallel line to a given line through a given point not on that line. • In non-Euclidean geometry there are exactly two parallel lines, in Lobachevsky’s sense, which implies that there are infinite ...
... Finally he shows that the dichotomy extends to parallels. • In Euclidean geometry there is exactly one parallel line to a given line through a given point not on that line. • In non-Euclidean geometry there are exactly two parallel lines, in Lobachevsky’s sense, which implies that there are infinite ...
Geometry practice lesson 9.5 worksheet answers
... Littell Geometry Practice Workbook ISBN: 9780618736959 / 0618736956. GeometryDiscovering An Investigative Approach Practice Your Skills with Answers DG4PSA_894_fm.qxd 11/1/06 11:16 AM Page i Solutions in Geometry: Homework Practice Workbook (9780078908491). 12-1: Representations of Three-Dimensional ...
... Littell Geometry Practice Workbook ISBN: 9780618736959 / 0618736956. GeometryDiscovering An Investigative Approach Practice Your Skills with Answers DG4PSA_894_fm.qxd 11/1/06 11:16 AM Page i Solutions in Geometry: Homework Practice Workbook (9780078908491). 12-1: Representations of Three-Dimensional ...
ROCKY FORD CURRICULUM GUIDE SUBJECT: Geometry GRADE
... can be transformed, and those transformations can be described and analyzed mathematically ...
... can be transformed, and those transformations can be described and analyzed mathematically ...
ROCKY FORD CURRICULUM GUIDE SUBJECT: Geometry GRADE
... Derive the formula for the area of a sector. I d. Understand similarity in terms of similarity transformations. i. Verify experimentally the properties of dilations given by a center and a scale factor. 1. Show that a dilation takes a line not passing through the center of the dilation to a parallel ...
... Derive the formula for the area of a sector. I d. Understand similarity in terms of similarity transformations. i. Verify experimentally the properties of dilations given by a center and a scale factor. 1. Show that a dilation takes a line not passing through the center of the dilation to a parallel ...