Geometry Honors - Santa Rosa Home
... Apply transformations (translations, reflections, rotations, dilations, and scale factors) to polygons. to determine congruence, similarity, and symmetry. Know that images formed by translations, reflections, and rotations are congruent to the original shape. Create and verify tessellations of the p ...
... Apply transformations (translations, reflections, rotations, dilations, and scale factors) to polygons. to determine congruence, similarity, and symmetry. Know that images formed by translations, reflections, and rotations are congruent to the original shape. Create and verify tessellations of the p ...
HS Standards Course Transition Document 2012
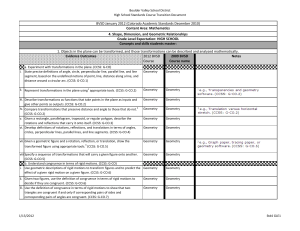
... 1. Objects in the plane can be transformed, and those transformations can be described and analyzed mathematically. Evidence Outcomes 2012 BVSD 2009 BVSD Notes Course Course name name a. Experiment with transformations in the plane. (CCSS: G-CO) i. State precise definitions of angle, circle, perpend ...
... 1. Objects in the plane can be transformed, and those transformations can be described and analyzed mathematically. Evidence Outcomes 2012 BVSD 2009 BVSD Notes Course Course name name a. Experiment with transformations in the plane. (CCSS: G-CO) i. State precise definitions of angle, circle, perpend ...
Holt McDougal Geometry 4-7
... 4-7 Triangle Congruence: CPCTC Check It Out! Example 1 A landscape architect sets up the triangles shown in the figure to find the distance JK across a pond. What is JK? One angle pair is congruent, because they are vertical angles. ...
... 4-7 Triangle Congruence: CPCTC Check It Out! Example 1 A landscape architect sets up the triangles shown in the figure to find the distance JK across a pond. What is JK? One angle pair is congruent, because they are vertical angles. ...
3-3 Notes
... 3-3 Proving Lines Parallel Example 1A: Using the Converse of the Corresponding Angles Postulate Given the information to show that ℓ || m. ...
... 3-3 Proving Lines Parallel Example 1A: Using the Converse of the Corresponding Angles Postulate Given the information to show that ℓ || m. ...
If the lines are parallel, then
... • CN-1 Things which are equal to the same thing are also equal to one another. • CN-2 If equals be added to equals, the wholes are equal. • CN-3 If equals be subtracted from equals, the remainders are equal. • CN-4 Things which coincide with one another are equal to one another. • CN-5 The whole is ...
... • CN-1 Things which are equal to the same thing are also equal to one another. • CN-2 If equals be added to equals, the wholes are equal. • CN-3 If equals be subtracted from equals, the remainders are equal. • CN-4 Things which coincide with one another are equal to one another. • CN-5 The whole is ...
2.5 Angle Relationships powerpoint
... 3. Draw XY . 4. What kind of angles did you create? 5. Measure the two angles with your protractor. What do you notice? Serra - Discovering Geometry Chapter 2: Reasoning in Geometry ...
... 3. Draw XY . 4. What kind of angles did you create? 5. Measure the two angles with your protractor. What do you notice? Serra - Discovering Geometry Chapter 2: Reasoning in Geometry ...
June 2016 Dear Students, The class you are scheduled for next year
... The class you are scheduled for next year is Geometry. To give you the best chance for success in Geometry, some preparation work is being recommended. Please watch the suggested videos (should you experience any difficulty) and complete the provided problems. While the number of problems is not lar ...
... The class you are scheduled for next year is Geometry. To give you the best chance for success in Geometry, some preparation work is being recommended. Please watch the suggested videos (should you experience any difficulty) and complete the provided problems. While the number of problems is not lar ...