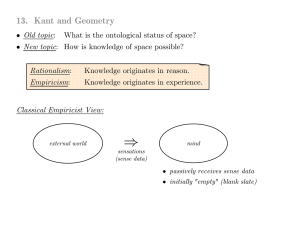
13.Kant and Geometry
... principles of mathematical determination would be nothing but perceptions. They would therefore all share in the contingent character of perception; that there should be only one straight line between two points would not be necessary, but only what experience always teaches." ...
... principles of mathematical determination would be nothing but perceptions. They would therefore all share in the contingent character of perception; that there should be only one straight line between two points would not be necessary, but only what experience always teaches." ...
Algebraic Geometry I
... Write up solutions to three of the problems (write as legibly and clearly as you can, preferably in LaTeX). 1. (Intersection Multiplicities.) Let C = V (f ) and D = V (g) be two distinct curves in A2 . Recall that the multiplicity of intersection mp (C, D) of C and D at p is defined as the dimension ...
... Write up solutions to three of the problems (write as legibly and clearly as you can, preferably in LaTeX). 1. (Intersection Multiplicities.) Let C = V (f ) and D = V (g) be two distinct curves in A2 . Recall that the multiplicity of intersection mp (C, D) of C and D at p is defined as the dimension ...
Non-Euclidean Geometry
... postulates. This ultimately gave rise to the discovery of non-Euclidean geometries in the 19th century. ...
... postulates. This ultimately gave rise to the discovery of non-Euclidean geometries in the 19th century. ...
The Word Geometry
... Uses as its parallel postulate any statement equivalent to the following: If l is any line and P is any point not on l , then there exists at least two lines through P that are parallel to l . ...
... Uses as its parallel postulate any statement equivalent to the following: If l is any line and P is any point not on l , then there exists at least two lines through P that are parallel to l . ...























